Bloc - Centre d'Estudis Edukat

Per a fer una cerca al bloc

Escriviu a la caixeta de cerca la paraula. (→)
Us apareixeran diferents entrades que la contenen.
Feu Ctrl+F per a cercar la paraula a la pàgina.
Si s’ha trobat més d’una pàgina, feu Ctrl+F a cada pàgina.

Consells per a estudiar bé

Dorm i menja bé.
Manté al dia l’horari i l’agenda personal d’estudi i un sistema d’arxiu ordenat i pulcre.
Fes una planificació futura com a mínim amb dues setmanes d’antelació dels deures i exàmens.
No memoritzis amb la intenció de només aprovar exàmens i cerca paraules al diccionari per comprendre els materials d’estudi.
Memoritzar és duplicar la feina, tampoc garanteix l’aprovat i podria ser la causa de situacions catastròfiques en els teus estudis.
Fes els deures i estudia el que has fet a classe a diari. Si fas l’ESO o Batxillerat i no estudies cada dia, podries tenir dificultats importants en els teus estudis.
Presenta els treballs, llegeix els llibres que se t’assignen i no xerris a classe.
No estudiïs per treure només un cinc, estudia per treure un deu.
Fes els deures i els exàmens sense nervis i repassa els exercicis abans d’entregar-los.
Prepara les consultes i dubtes que tinguis abans de venir reforç per aprofitar-ne millor les hores.
Porta els teus propis llibres, ordinador portàtil, calculadora, bolígrafs, llapis, gomes d’esborrar i tot el material necessari per fer la classe i marca’ls amb el teu nom.
Desconnecta el mòbil o posa’l en mode avió abans d’entrar a classe.
Aixeca el braç cada vegada que tinguis un dubte i t’atendrem tan aviat com ens sigui possible.
Les classes de reforç són un ajut pels teus estudis i un premi per a tu … aprofita-les.
Els resultats depenen sobretot de la teva dedicació personal diària i de la teva capacitat personal i, per tant, no podem garantir-te l’aprovat, però si treballes com a un professional és molt probable que aprovis.

Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?

Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.

Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons

1. Cinemàtica relativista

En mecànica relativista, el temps i la distància depenen de l’observador que els mesuri.

1.1 Transformacions de Lorentz:

El 1881, els físics nord-americans Michelson i Morley mesuraren la velocitat de la llum en diferents direccions i, sorprenentment, trobaren que era sempre la mateixa. No obstant això, les transformacions de Galileu indiquen que cap objecte pot tenir la mateixa velocitat respecte a dos observadors que es mouen uniformement (MRU).

Einstein resolguí aquesta paradoxa el 1905 establint que la velocitat de la llum és la mateixa per a qualsevol observador. És a dir, que l’interval de temps que transcorre entre dos esdeveniments depèn de l’observador que el mesuri.

Per tant, s’han d’ajustar les transformacions de Galileu perquè la velocitat de la llum sigui invariant. Dos observadors (O i O’) que es mouen uniformement amb una velocitat relativa u respecte a l’eix X ajusten els rellotges perquè t=t’=0. Si en l’instant t=0, cada observador emet un raig de llum en direcció al punt A:

\begin{matrix} Per a cada observador es compleix que r^{2} = x^{2} + y^{2} + z^{2}, essent r = ct . Per tant, \\ {\begin{matrix} \begin{matrix} r = ct \to {(ct)}^{2} = x^{2} + y^{2} + z^{2} (1) \\ r = ct' \to {(ct')}^{2} = x'^{2} + y'^{2} + z'^{2} (2) \end{matrix} \end{matrix} \\ Subtituint les equacions de les transformacions de Galileu en l'equació del segon observador: \\ x' = x - ut; y' = y; z' = z; t' = t \to x^{2} + y^{2} + z^{2} - 2 xut + u^{2} t^{2} \\ Per tant, les Transformacions de Galileu ara no funcionen perquè no es compleix la igualtat. \\ El terme 2 xut + u^{2} t^{2} conté temps i espai. Si ajustem x' i t' per fer que les equacions (1) i (2) coincideixin: \\ x' = k (x - ut) i t' = a (t - bx) : \\ k^{2} (x^{2} - 2 uxt + u^{2} t^{2}) + y^{2} + z^{2} = c^{2} a^{2} (t^{2} - 2 bxt + b^{2} x^{2}) \\ (k^{2} - b^{2} a^{2} c^{2}) x^{2} - 2 (k^{2} u - b a^{2} c^{2}) xt + y^{2} + z^{2} = (a^{2} - k^{2} \frac{u^{2}}{c^{2}}) c^{2} t^{2} \\ k^{2} \to b^{2} a^{2} c^{2} = 1, k^{2} u - b a^{2} c^{2} = 0, a^{2} - k^{2} \frac{u^{2}}{c^{2}} = 1 \\ Per tant, \\ k = a = \frac{1}{\sqrt{1 - u^{2} / c^{2}}}, b = u / c^{2} \\ {\begin{matrix} \begin{matrix} x' = k (x - ut) = \frac{x - ut}{\sqrt{1 - u^{2} / c^{2}}} \end{matrix} \\ y' = y \\ z' = z \\ t' = a (t - bx) = \frac{t - ux / c^{2}}{\sqrt{1 - u^{2} / c^{2}}} \end{matrix} \\ L'expressió \frac{1}{\sqrt{1 - u^{2} / c^{2}}} és el factor de Lorentz \\ Quan u ≪ c, s'obtenen les transformacions de Galileu. \end{matrix}

1. 2 Transformacions de velocitat

\begin{matrix} v_{x} = \frac{dx}{dt}, v_{y} = \frac{dy}{dt}, v_{z} = \frac{dz}{dt} \\ v'_{x} = \frac{dx'}{dt'}, v'_{y} = \frac{dy'}{dt'}, v'_{z} = \frac{dz}{dt'} \\ {\begin{matrix} \begin{matrix} dx' = \frac{dx - u dt}{\sqrt{1 - u^{2} / c^{2}}} = \frac{v_{x} - u}{\sqrt{1 - u^{2} / c^{2}}} dt \\ dy' = dy \\ dz' = dz \\ dt' = \frac{dt - u dx / c ²}{\sqrt{1 - u^{2} / c^{2}}} \end{matrix} \end{matrix} \to {\begin{matrix} \begin{matrix} v'_{x} = \frac{dx'}{dt'} = \frac{v_{x} - u}{u - v_{x} / c^{2}} \\ v'_{y} = \frac{dy'}{dt'} = \frac{v_{y} \sqrt{1 - u^{2} / c^{2}}}{1 - u v_{x} / c^{2}} \\ v'_{z} = \frac{dz'}{dt'} = \frac{v_{z} \sqrt{1 - u^{2} / c^{2}}}{1 - u v_{x} / c^{2}} \end{matrix} \end{matrix} \end{matrix}

Si considerem que el moviment sols és en la direcció de l’eix $X $ i anomenem $v$ a $v_x$

v ’ = \frac{v_{x} - u}{u - v_{x} / c^{2}}, v ’_{y} = v ’_{z} = 0

1. 3 Conseqüències de les Transformacions de Lorentz

1.3.1 Temps i espai propi

Anomenem longitud pròpia $L_0$ a la longitud mesurada per l’observador que és en el mateix sistema de referència que l’objecte. En aquest cas, l’observador i l’objecte tindran una velocitat relativa $u=0.$

Anomenem temps propi $\tau, t_0$ a l’interval de temps que mesura l’observador pel qual dos esdeveniments ocorren en la mateixa posició.

La longitud o temps no propis els indiquem per L’, t’.

1.3.2 Contracció de la longitud

Per a fer la mesura de la longitud d’un objecte que és en MRU, l’observador en repòs ha d’emetre els dos rajos de llum simultàniament.

Per a un observador $O’$, la longitud de la barra serà $L’=x’_b-x’_a$

Però, per a l’observador $O$ la longitud serà $L_0=x_b-x_a$

\begin{matrix} x'_{a} = \frac{x_{a} - ut}{\sqrt{1 - u ² / c ²}}, x'_{b} = \frac{x_{b} - ut}{\sqrt{1 - u ² / c ²}} \to L' = \frac{x_{b} - x_{a}}{\sqrt{1 - u ² / c ²}} = \frac{L_{0}}{\sqrt{1 - u ² / c ²}} \\ L_{0} γ = L' \\ (L_{0} és la longitud pròpia i u és la velocitat relativa entre els observadors i c és la velocitat de la llum) \end{matrix}

Com que $γ<0$, la longitud mesurada per l’observador $O$, que veu la barra en moviment, és més petita que la mesurada per l’observador $O’$, que veu l’objecte en repòs. És a dir, que els objectes en moviment semblen més curts.

1.3.3 Dilatació temporal

Si dos observadors en moviment relatiu mesuren la separació temporal entre dos esdeveniments, trobaran valors diferents. Considerant que un dels dos observadors mesura ambdós esdeveniments sense moure’s:

\begin{matrix} Δ t' = \frac{Δ t_{0}}{\sqrt{1 - {(u / c)}^{2}}} = Δ t_{0} \frac{1}{\sqrt{1 - β^{2}}} \\ Δ t' = \frac{Δ t_{0}}{γ} \end{matrix}

Cinemàtica

Introducció

La cinemàtica és una branca de la física mecànica que estudia el moviment dels objectes i l’anàlisi de les trajectòries que formen. Si la dimensió de l’objecte és molt més petita que la de la trajectòria, el tractem com un punt o una partícula sense dimensions. Per exemple, considerarem una molècula com una partícula en moviment, però no seria adequat tractar les marees com a partícules si en volguéssim estudiar el moviment.

El moviment és un canvi de posició en el temps. Pot ser rectilini o circular (de translació, de rotació o de vibració) en una, dues o tres dimensions i és relatiu a l’observador. L’expressarem en coordenades cartesianes, esfèriques o cilíndriques (tot i que en mecànica relativista s’usa la geometria hiperbòlica) per tal que els càlculs siguin més senzills.

La trajectòria d’una partícula és el camí que segueix mentre es mou i està formada per moviments lineals i curvilinis.

En aquesta entrada estudiarem el moviment lineal i circular en una i dues dimensions fent ús del càlcul vectorial i escalar. Les magnituds del moviment lineal són: la posició, la velocitat, l’acceleració i el temps. Les tres primeres són magnituds vectorials, però la darrera és escalar.

En les equacions escalars, el signe de les magnituds vectorial indica el sentit del vector segons el criteri de signes dels eixos de coordenades (amunt, dreta: positiu, avall, esquerra: negatiu). Dos vectors de sentits diferents es resten, mentre que si tenen el mateix, se sumen. En conseqüència, si el vector velocitat i el vector acceleració tenen el mateix sentit, la partícula accelerarà, però si tenen sentit diferent, frenarà.

Per a resoldre un exercici de cinemàtica, cal escriure abans de res les equacions de cada partícula. A continuació, farem els càlculs que calguin per a respondre les qüestions de l’exercici.

2.1 Posició

La posició d’una partícula són les coordenades del punt (x,y) on és en un instant mesurades des de l’origen del sistema de referència triat.

Quan una partícula canvia de posició $(\vec{x})$ diem que ha transcorregut un temps (”t”).

$
\displaystyle{
\vec{r}=x \vec{i}+y \vec{j}+z \vec{k}\\
\Delta \vec {r}=\vec {{r}_{2}}-\vec {{r}_{1}}\\
}
$

El canvi de posició d’una partícula és el ”desplaçament” $(\Delta \vec{r}=\vec{x}_{2}-\vec{x}_{1})$ El mòdul d’aquest vector és la distància que ha recorregut (”d”).

Exemple:

$
\displaystyle{
\vec{r_{1}}=\left(3\vec{i}-4\vec{j}+5\vec{k}\right)
\\
\vec{{r}_{2}}=\left(2\vec{i}+2\vec{j}-8\vec{k}\right)
\\
\mathrm{\Delta }\vec{r}=\vec{{r}_{2}}-\vec{{r}_{1}}=\left(2\vec{i}+2\vec{j}-8\vec{k}\right)-\left(3\vec{i}-4\vec{j}+5\vec{k}\right)=\left(-1\vec{i}+6\vec{j}-13\vec{k}\right)
\\
d=| \vec r|=\sqrt{(-1)^2+(+6)^2+(-13)^2}=\sqrt{206}
}
$

2.2 Velocitat

La velocitat d’una partícula és el vector desplaçament dividit pel temps que triga a moure’s entre dos punts i ens indica la rapidesa amb la qual canvia de posició amb el temps. Per tant, és un vector que té la mateixa direcció i sentit que el vector desplaçament i sempre és tangent a la trajectòria en cada instant.

La velocitat mitjana és el desplaçament total que ha fet la partícula durant un període de temps, però no ens informa dels detalls del moviment. Per exemple, podria haver-se desplaçat a la mateixa velocitat durant tot el trajecte, o bé haver-se parat, frenat i accelerat.

$\displaystyle{\vec{{v}_{m}}=\frac{\mathrm{\Delta }\vec{r}}{\mathrm{\Delta }t}}$

Si aquesta partícula es mou amb una velocitat variable, ens caldrà determinar a quina velocitat es desplaça en cada instant de la trajectòria. Definim la velocitat instantània com el límit del vector desplaçament $\mathrm{\Delta }\vec{r}$ en un interval de temps infinitament petit:

$\displaystyle{\vec{{v}_{i}}=\underset{\mathrm{\Delta }\rightarrow 0}{\lim }\frac{\mathrm{\Delta }\vec{r}}{\mathrm{\Delta }t}=\underset{\mathrm{\Delta }\rightarrow 0}{\lim }\frac{\vec{r}\left(t+\mathrm{\Delta }t\right)-\vec{r}\left(t\right)}{\mathrm{\Delta }t}=\frac{\mathit{d \vec r}}{\mathit{dt}}}$

El vector velocitat instantània és el pendent de la funció posició en un punt (vegeu gràfic de l’apartat 2.1).

Com que la velocitat és una magnitud vectorial, el canvi pot ser del mòdul, de la direcció o del sentit, però la direcció i sentit de $\vec v_i$ serà la de $ \Delta \vec r$ quan els dos punts de posició estiguin infinitament a prop.

Per tant, com que $\vec{r}=x\vec{i}+y\vec{j}+z\vec{k}$

$
\displaystyle{
\vec{{v}_{i}}=\frac{d\vec{r}}{\mathit{dt}}=\frac{\mathit{dx}}{\mathit{dt}}\vec{i}+\frac{\mathit{dy}}{\mathit{dt}}\vec{j}+\frac{\mathit{dz}}{\mathit{dt}}\vec{k}={v}_{x}\vec{i}+{v}_{y}\vec{j}+{v}_{z}\vec{k}
}
$

2.3 Acceleració

L’acceleració és la rapidesa amb la qual canvia la velocitat (mòdul, direcció o sentit) d’una partícula amb el temps.

L’acceleració mitjana és la variació de velocitat de la partícula en un interval de temps. Consegüentment, té la mateixa direcció i sentit que la velocitat, però tampoc ens informa dels detalls del moviment durant el desplaçament.

$\displaystyle{{a}_{m}=\frac{\mathrm{\Delta }\vec{v}}{\mathrm{\Delta }t}}$

Però, quan l’acceleració és variable, per tal de determinar-la en un instant determinat del temps, definim l’acceleració instantània com el canvi de la velocitat en un instant infinitament petit de temps:

$\displaystyle{\vec{a}=\underset{\mathrm{\Delta }t\rightarrow 0}{\lim }\frac{\mathrm{\Delta }\vec{v}}{\mathrm{\Delta }t}=\frac{d\vec{v}}{\mathit{dt}}}$

i, per tant,

$\displaystyle{
\vec a=\frac{dv_x}{dt}\vec i+\frac{dv_y}{dt}\vec j+\frac{dv_z}{dt}\vec k=a_x \vec i+a_y \vec j+a_z \vec k
}
$

Exemple:

\(
\displaystyle{
\text{L’equació vectorial de desplaçament d’una partícula és:}
\\[0.5cm]
\vec{r(t)}=(5+12{t}^{2}) \vec{i}-2t \vec{j}+({t}^{3}+8t) \vec{k}
\\[0.5cm]
\text{a) Quina és la posició en els instants t=2 i 5 segons i quin ha estat el desplaçament?}
\\[0.5cm]
\vec{r(2)}=(5+12{(2)}^{2})\vec{i}-2(2)\vec{j}+(t{(2)}^{3}+8(2))\vec{k}=
\\
53\vec{i}-4\vec{j}+24\vec{k}
\\
\vec{r(5)}=(5+12{(5)}^{2})\vec{i}-2(5)\vec{j}+({(5)}^{3}+8(5))\vec{k}=305\vec{i}-10\vec{j}+165\vec{k}\\
\mathrm{\Delta }\vec{r}=\vec{r}(5)-\vec{r}(2)=(305\vec{i}-10\vec{j}+165\vec{k})-(53\vec{i}-4\vec{j}+24\vec{k})=252\vec{i}-6\vec{j}+141\vec{k}
\\[0.5cm]
\text{b) Quina és la velocitat en els instants t=3 i 5 i quina és la velocitat mitjana?}
\\[0.5cm]
\vec{v(t)}=d\frac{\vec{r(t)}}{\mathit{dt}}=\frac{d}{\mathit{dt}}[(5+12{t}^{2})\vec{i}-2t\vec{j}+({t}^{3}+8t)\vec{k}]=
\\
24t\vec{i}-2\vec{j}+(3{t}^{2}+8)\vec{k}\\
\vec{v(3)}=24(3)\vec{i}-2\vec{j}+\lbrack 3{(3)}^{2}+8\rbrack \vec{k}=
\\
72\vec{i}-2\vec{j}+35\vec{k}\\
\vec{v(5)}=24(5)\vec{i}-2\vec{j}+\lbrack 3{(5)}^{2}+8\rbrack \vec{k}=
\\
120\vec{i}-2\vec{j}+83\vec{k}\\
\mathrm{\Delta }\vec{v}=(120\vec{i}-2\vec{j}+83\vec{k})-(72\vec{i}-2\vec{j}+35\vec{k})=
\\
48\vec{i}+48\vec{k}\\
\vec{{v}_{m}}=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\frac{48\vec{i}+98\vec{k}}{5-3}=\frac{48}{5}\vec{i}+\frac{48}{3}\vec{k}
\\[1cm]
\text{c) Calculeu el vector acceleració:}
\\[0.5cm]
a(t)=\frac{{d}^{2}\lbrack \vec{r}(t)\rbrack }{\mathit{dt}^{2}}=d\frac{\vec{v}(t)}{\mathit{dt}}=24\vec{i}+6t\vec{k}
}
\)

2. Moviment lineal en una dimensió

2.1 Horitzontal

Si ”a=0”, la velocitat és constant i el moviment és anomenat MRU o moviment rectilini uniforme.

Si ”a ≠ 0” i és constant, el moviment és anomenat MRUA o moviment rectilini uniformement accelerat.

Si l’acceleració és constant, la velocitat mitjana $\displaystyle{\bar{v}=\frac{v_f+v_0}{2}}$ en qualsevol interval també és constant.

$
\displaystyle{
\text{Si substituïm } t=\frac{v_f-v_0}{a} \text{ a } x=x_o+\bar v t
\\
v_f^{2}-v_0^2=2a(x-x_0)
\\[1cm]
\text{I com que,}
\\[0.5cm]
\bar v= \frac {1}{2}(v_f+v_0) \text{ i }v_f=v_0+at
\\
x=x_0+\bar v t \rightarrow x=x_0+\frac {1}{2}(v_f+v_0)t
\\
x=x_0+\frac{1}{2}[(v_0+at)+v_0]t
\\
x=x_0+v_0t+\frac {1}{2}at^2
}
$

Per tant, les equacions de moviment horitzontal són:

$\displaystyle{\begin{array}{c}x={x}_{0}\pm {v}_{0}\cdot t\pm \frac{1}{2}\mathit{at}\mathrm{{^2}}\\
{v}_{f}={v}_{0}\pm \mathit{at}\end{array}}$

Exemple:

En quina posició i temps es trobaran els mòbils següents?

\(
\displaystyle{
\text{1. Tranformem totes les dades SI:}
\\[0.5cm]
90\frac{{Km}}{h}\cdot \frac{1000\text{m}}{1\text{Km}}\cdot \frac{1\text{h}}{3600\text{s}}=25\text{m/s}
\\[0.5cm]
\text{1. Escrivim les equacions de moviment de cada partícula:}
\\[0.5cm]
{x}_{A}={x}_{0A}+{v}_{0A}t \rightarrow {x}_{A}=0+25t
\\
{v}_{{fA}}={v}_{0A}=25\text{m/s}
\\[0.5cm]
\text{Però, com que la partícula A haurà trigat en recórrer 100}m{\colon }
\\[0.5cm]
100=0+25t \rightarrow t=4\text{s}
\\[0.5cm]
\text{llavors,}
\\[0.5cm]
{x}_{A}=100+25(t-4)
\\
{x}_{B}={x}_{0B}+{v}_{0B}t+\frac{1}{2}{{at}}^{2}=0+0t+\frac{1}{2}3t{{^2}}=\frac{3}{2}{t}^{2}
\\
{v}_{{fB}}={v}_{0B}+{at}=0+3t=3t
\\[0.5cm]
\text{2. Com que la posició i el temps de trobada és el mateix per a ambdues:}
\\[0.5cm]
{x}_{A}={x}_{B} \rightarrow 100+25(t-4)=\frac{3}{2}{t}^{2} \rightarrow \frac{3}{2}{t}^{2}-25t=0
\\
t=16.\hat{6} \text{s} \rightarrow {x}_{A}={x}_{B}=\frac{3}{2}{(16.\hat{6})}^{2}={416.\hat 6}\text{m}
\\[0.5cm]
\text{I la velocitat de la moto serà: }{v}_{B}=3 \cdot (16.\hat{6})=3(16.\hat{6})={49.8}\text{m/s}
}
\)

La representació gràfica de la posició, la velocitat i l’acceleració en funció del temps de cada moviment és:

2.2 Vertical (caiguda lliure)

Les equacions de moviment de la caiguda lliure d’una partícula, són:

$\displaystyle{
y={y}_{0}\pm {v}_{0}\cdot t-\frac{1}{2}g{t}^{2}
\\
{v}_{f}={v}_{0}-gt
}
$

I, similarment al cas de moviment horitzontal:

$\displaystyle{
{v}_f^{2}={v}_{0}^{2}+2a\cdot (y-y_0)}$

Durant el camí de pujada i de baixada, canvia el mòdul i el sentit, però no pas la direcció del vector velocitat. La direcció, sentit i el mòdul del vector acceleració $\vec{g}$ és sempre el mateix.

Exemples:

$\displaystyle{
\text{1.Escrivim les equacions de moviment:}
\\[0.5cm]
y={y}_{0}+{v}_{0}t-\frac{1}{2}g{t}^{2}
\\
{v}_{f}={v}_{0}-gt
\\[0.5cm]
\text{2. Com que quan } t=2, {v}_{f}=+30\text{m/s}
\\[0.5cm]
{v}_{0}={v}_{f}+gt=30+9.8\cdot 2=49.6\text{m/s}
\\[0.5cm]
\text{i, quan arriba a dalt de tot:}
\\[0.5cm]
{v}_{f}=0={v}_{0}-gt=49.6-9.8t \rightarrow t=\frac{49.6.4}{9.8}=5.06\text{s}
\\[0.5cm]
\text{Per tant, l’alçada màxima que assoleix és:}
\\[0.5cm]
y={y}_{0}+{v}_{0}t-\frac{1}{2}9.8{t}^{2}=0+49.6 \cdot 5.06-4.9 \cdot {5.06}^{2}=125.52\text{m}
}
$

Moviment en el pla (dues dimensions)

3.1 Moviment parabòlic

És un moviment en el qual el component horitzontal és un MRU (2.11) i el vertical un MRUA (2.1.2).

Hi ha tres punts de referència (A, B, C) que ens serviran per a plantejar les equacions de moviment i resoldre l’exercici:

$\displaystyle{
A:
\\[0.5cm]
y=0,\\
{v}_{x}=v_0\cdot \cos \theta \enspace (\mathit{constant},\mathit{MRU}),\\
{v}_{y\mathit{m\grave{a}x}}={v}_{0}\cdot \sin \theta \enspace (\mathit{MRUA})
\\[0.5cm]
B\mathrm{\colon }
\\[0.5cm]
y_{\mathit{m\grave{a}x}}=h,\\
{v}_{x}={v}_{0}\cdot \cos \theta \enspace (\mathit{constant},\mathit{MRU}),\\
{v}_{y}=0(\mathit{MRUA})
\\[0.5cm]
C\mathrm{\colon }
\\[0.5cm]
y=0,\\
{v}_{x}=v\cdot \cos \theta (\mathit{constant},\mathit{MRU}),\\
{v_{y\mathit{m\grave{a}x}}}=-{v}_{0}\cdot \sin \theta \enspace (\mathit{MRUA})\\
R(\mathit{abast})={v}_{x}\cdot t
}
$

Exemple:

$\displaystyle{
\text{1. Les equacions de moviment, són:}
\\[0.5cm]
\text{a) Per al moviment vertical:}
\\[0.5cm]
y={y}_{0}\pm {v}_{0y}t-\frac{1}{2}g{t}^{2}
\\
{v}_{\mathit{fy}}={v}_{0y}-gt
\\[0.5cm]
\text{b. Per al moviment horitzontal:}
\\[0.5cm]
x={x}_{0}\pm {v}_{0x}t
\\[0.5cm]
{v}_{f}={v}_{0}
\\[0.5cm]
\text{2. Subtituint amb les dades que tenim:}
\\[0.5cm]
(i) \enspace y=40+30\cdot \sin (35)t-\frac{1}{2}9.8{t}^{2}
\\
(\mathit{ii}) \enspace {v}_{fy}=30\cdot \sin (35)-9.8t
\\
(\mathit{iii}) \enspace 20=0+30\cdot \cos (35)t
\\
(\mathit{iv}) \enspace v_{fx}=30\cdot \cos (35)
\\[0.5cm]
\text{3. Resolem els sistema d’equacions:}
\\[0.5cm]
\text{de (iii): }t=\frac{20}{30\cdot \cos (35)}=0.814s\\
\text{i, substituint a (i): }y=40+30\sin (35)\cdot 0.814-4.9{(0.814)}^{2}=\mathrm{50.76}\text{m}
\\[0.5cm]
\text{Quan arribi al terra, hauran transcorregut:}
\\[0.5cm]
0=40+30\sin (35)t-4.9{t}^{2} \rightarrow t=6.27\text{s}
}
$

3.2 Moviment circular

La trajectòria d’una partícula està formada de moviments lineals i circulars. Segons la llei d’inèrcia de la dinàmica de Newton, per tal de canviar-la, hi ha d’haver una força externa neta que hi actuï. Aquesta força modificarà la direcció o el sentit de la velocitat, però, si és perpendicular, farà que segueixi un camí circular.

Els vectors de velocitat i acceleració centrípeta sempre són tangent i perpendicular a la trajectòria respectivament (l’acceleració centrípeta sempre es dirigeix cap al centre de gir). El mòdul dels vectors és constant, però la direcció d’ambdós canvia constantment.

Quan la distància entre $P$ i $P’$ és molt petita, el vector velocitat apunta cap al centre de $O$ Per tant, com que els triangles isòsceles de velocitats

$
\displaystyle{
(v_t,v_t,\Delta v)
}
$

i

$(O, P, P’)$

són semblants i, considerant que $s\approx v \cdot \mathrm{\Delta }t$

$\displaystyle{
\frac{\mathrm{\Delta }v}{{v}_{t}}\approx \frac{v\cdot \mathrm{\Delta }t}{r}\rightarrow {a}_{c}=\frac{\mathrm{\Delta }v}{t}\approx \frac{{v}_{t}^{2}}{r}}$

I, quan $\mathrm{\Delta }t\rightarrow 0,$aquesta expressió és exacta:

$\displaystyle{{a}_{c}=\underset{\mathrm{\Delta }t\rightarrow 0}{\lim }\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}.}$

Exemple:

$
\displaystyle{
\text{Dades}
\\[0.5cm]
R=5\mathit{cm},\enspace {v}_{0}=0\text{m/s}, \enspace \alpha =10\text{rad/s},\enspace t=30\text{s}
\\[0.5cm]
\text{1. La velocitat angular, lineal, l’acceleració centrípeta i tangencial despreś de 30 s és:}
\\[0.5cm]
w={w}_{0}+\alpha t=0+10\cdot 30=300\text{rad/s}\rightarrow v=w \cdot R=300 \cdot \mathrm{0,05}=15\text{m/s}
\\
{a}_{c}=\frac{{v}^{2}}{R}=\frac{{15}^{2}}{0.05}=4500m/s\mathrm{{^2}},\alpha ={a}_{t}\cdot R\rightarrow {a}_{t}=\frac{10}{0.05}=200m/s\mathrm{{^2}}
\\[0.5cm]
\text{3. L’angle recorregut després de 30 s és:}
\\[0.5cm]
\theta ={\theta }_{0}+{w}_{0}t+\frac{1}{2}\alpha {t}^{2}=0+0+\frac{1}{2}\cdot 10 \cdot {30}^{2}=4500\text{rad, és a dir,}
\\
4 500\text{rad}\cdot \frac{1\text{volta}}{2\pi \text{rad}}=716\text{ voltes senceres}
}
$

3.3 Moviment relatiu

3.3.1 Transformacions de Galileu:

Si en un sistema de referència $S’$ que es mou a velocitat constant respecte a un altre de fix (per exemple, la Terra), una partícula (per exemple un avió) es desplaça del punt $A$ fins al punt $B$

$
\displaystyle{
\vec{r}=\vec{r}\text{‘}+\vec{u}\cdot t
\\
\frac{d\vec{r}}{\mathit{dt}}=\frac{d\vec{r}\text{‘}}{\mathit{dt}}+\frac{d\vec{u}\cdot t}{\mathit{dt}}
\\
v=v\text{‘}+u
}
$

$\displaystyle{\frac{d\vec{r}}{\mathit{dt}}}$ és la velocitat instantània de la partícula mesurada en el sistema de referència $S$ i $\displaystyle{\frac{d\vec{r}\text{‘}}{\mathit{dt}}}$la mesurada en el $S’$ Per tant, la velocitat d’una partícula amb relació al sistema fix $S$ és la suma vectorial de la velocitat respecte al $S’ $i la relativa de $S’$ respecte a $S$

En mecànica clàssica, el canvi de la velocitat d’una partícula vist des de sistemes de referència diferents és el mateix per a tots els observadors i, en conseqüència, també mesuraran la mateixa acceleració (a=a’):

$
\displaystyle{
\frac{d\vec{v}}{\mathit{dt}}=\frac{d\vec{v}}{\mathit{dt}}+\frac{d\vec{u}}{\mathit{dt}}
\\
\text{però, com que }\frac{d\vec{u}}{\mathit{dt}}=0\rightarrow \frac{d\vec{v}}{\mathit{dt}}=\frac{d\vec{v}}{\mathit{dt}}\left(a=a\text{‘}\right)
}
$

Apèndix

Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?

Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.

Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons

$\begin{matrix} \end{matrix}$

Dinàmica

Instruccions abans de començar

Introducció

Les forces són les accions que causen el moviment i el canvi de moviment de les partícules. La dinàmica és l’estudi de les lleis que produeixen aquests canvis.

Primer, les estudiarem quan actuen sobre partícules. Després introduirem el concepte de centre de masses per tal de tractar l’efecte de les forces sobre un sòlid. Considerarem que són de magnitud i direcció constants.

La mecànica clàssica estudia l’efecte d’una força que actua sobre partícules o sòlids que es mouen a velocitats petites comparades amb la velocitat la llum (v<0.1 c). És a dir, que coneixent-ne les propietats (massa, càrrega, velocitat inicial, etc.) estudia com canviarà l’estat del moviment inicial de l’objecte.

Com que la força és una magnitud vectorial, és important conèixer bé el càlcul vectorial.

1. Lleis de la dinàmica (translacional)

Newton, que va néixer a Anglaterra el mateix any que morí Galileu, formulà les lleis de la mecànica clàssica a partir de les idees d’aquest i de físics anteriors. Les va presentar el 1686 en el Principia Philosophiae Naturalis (Principis de Filosofia Natural).

Galileu afirmà que cal una força externa per a canviar la velocitat d’un cos. Aquesta força farà que en canviï la velocitat i l’acceleració que, sent vectors, depenen del sistema de referència triat per a mesurar-les.

Les forces de la natura són de naturalesa electromagnètica, nuclear (feble i forta) i gravitacional.

La definició clàssica de matèria és la quantitat de matèria que conté un objecte, tot i que no és del tot correcta, perquè la matèria es forma sobretot a partir de fenòmens d’interacció quàntica.

1.1 Primera llei de Newton, la llei de la inèrcia:

”Si no actua cap força externa neta sobre un cos, es conservarà l’estat de moviment a causa de la inèrcia (a=0). “

La inèrcia és la resistència d’un cos a canviar el seu estat de moviment quan no hi actua cap força neta, per tant, es mantindrà en repòs o movent-se a velocitat constant (a=0). Com més massa tingui un objecte, més resistència (inèrcia) farà per què no canviï l’estat de moviment.

1.2 Segona llei de Newton, llei fonamental de la dinàmica:

”Quan apliquem una força sobre un objecte, aquest objecte s’accelera de forma directament proporcional a la força aplicada i inversament proporcional a la massa de l’objecte: $\displaystyle{a=\frac{1}{m}\cdot F}$

Si fem l’experiment d’aplicar una força de la mateixa magnitud i sentit sobre diferents cossos, observarem que es produeix una acceleració en cadascun que varia segons la massa. Per tant, la massa és una magnitud (escalar) directament relacionada amb la inèrcia. És a dir:

\begin{array}{c}F=\displaystyle{{m}_{1}\cdot {a}_{1}={m}_{2}\cdot {a}_{2}\mathrm{…}\rightarrow F=m\mathrm{.}a}\end{array}

El pes és la força d’atracció que fa la Terra sobre els objectes que són dins de l’atmosfera terrestre.

Com que la força també és una magnitud vectorial (és el resultat de multiplicar un escalar per un vector), per a usar-la escalarment l’haurem de descompondre en les seves components del pla o de l’espai fent ús de la trigonometria:

\begin{array}{c}{F}_{x}=m\cdot {a}_{x},{F}_{y}=m\cdot {a}_{y},{F}_{z}=m\cdot {a}_{z}\end{array}

1.3 Tercera llei de Newton, llei d’acció i reacció

”A tota força d’acció se li oposa sempre una força de reacció d’igual magnitud i de sentit contrari.”

L’acció mútua entre dos cossos en contacte és de la mateixa magnitud i de sentit contrari, però tant l’acció com la reacció actuen sobre cossos diferents i, per tant, la resultant és diferent de zero i el moviment pot ser accelerat:

1.4 Com es resolen els exercicis de dinàmica

Per a resoldre exercicis de dinàmica, seguirem en aquest ordre els següents passos:

Fer el diagrama de blocs o del sòlid lliure (dibuix)
Fer el diagrama de forces per a cada bloc o massa.
Plantejar el sistema d’equacions per a cada bloc o massa.

Exemple:

\begin{matrix} \sum F_{x} = T - P_{1 x} - f = m_{1} \cdot a \\ T - P \cdot \sin (α) - μ \cdot P \cdot \cos (α) = m_{1} \cdot a \\ T - m_{1} \cdot g \cdot \sin (α) - μ \cdot m_{1} \cdot g \cdot \cos (α) = m_{1} \cdot a \\ T - m_{1} \cdot g \cdot [\sin (α) - μ \cdot \cos (α)] = m_{1} \cdot a \\ T = m_{1} \cdot a + m_{1} \cdot g \cdot [\sin (α) - μ \cdot \cos (α)] \\ \sum F_{y} = N - P_{1 y} = 0 \\ N - m_{1} \cdot g \cdot \cos (α) = 0 \end{matrix}

\begin{matrix} \begin{matrix} \sum F_{y} = T - P_{2} = - m_{2} \cdot a \\ T = m_{2} \cdot g - m_{2} \cdot a = m_{2} \cdot (g - a) \end{matrix} \\ Per tant, \\ m_{1} \cdot a + m_{1} \cdot g \cdot [\sin (θ) - μ \cos (θ)] = m_{2} \cdot (g - a) \\ a = \frac{- m_{1} \cdot g \cdot [\sin (θ) - μ \cos (θ)] + m_{2} \cdot g}{m_{2} + m_{1}} \end{matrix}

Dinàmica Newton, dinàmica moviment circular

\begin{matrix} Del  bloc 1: \\ F_{c} = m \cdot a_{c} = \frac{m \cdot v^{2}}{R} \\ Del bloc 2: \\ {\begin{matrix} F_{c} = T \\ P = T \end{matrix} \to T = \frac{m \cdot v^{2}}{R} = M \cdot g \to v = \sqrt{\frac{M \cdot g \cdot R}{m}} \end{matrix}

{\begin{matrix} P = F \cdot \cos θ \\ F_{c} = F \cdot \sin θ = \frac{m \cdot v^{2}}{R} \to v = \sqrt{\frac{F \cdot \sin θ \cdot R}{m}} = \sqrt{\frac{P \cdot \tan θ \cdot R}{m}} \\ \sin θ = \frac{R}{L} \to θ = \arcsin \frac{R}{L} \end{matrix}

2. Forces

Les forces poden ser de contacte o a distància:

a) De contacte: de fricció, tensions, forces normals, de resistència a l’aire, forces aplicades, de molles.

b) A distància: gravitacionals, electromagnètiques.

Les forces naturals són la gravitatòria, l’electromagnètica, la nuclear feble (responsable de la desintegració radioactiva) i la nuclear forta (que permet que els protons i els neutrons es mantinguin units dins el nucli. Apareixen a conseqüència de les interaccions entre partícules atòmiques elementals).

2.1 Llei de Hooke

La llei de Hooke és una força de contacte elàstica en la qual la força de recuperació d’una molla comprimida o estirada és proporcional a la distància de compressió o estirament.

És vàlida sempre que la distància de compressió o d’estirament sigui petita comparada amb la compressió o estirament total possible de la molla i que la força no superi un límit (límit elàstic, ”E”) de manera que la molla es deformi permanentment. De totes maneres, alguns materials no compleixen la llei de Hooke encara que no hagin arribat al límit elàstic.

Generalitzant la llei, direm que la deformació d’un objecte elàstic complex és proporcional a la tensió aplicada, és a dir, que considerem que es comporta com una molla sotmesa a tracció o compressió. En aquest cas, la llei de Hooke $F=-k.Δx$ d’una molla es pot assimilar a l’elasticitat d’una barra de material elàstic de longitud $L$ i àrea $A$

\begin{matrix} F = σ A = ε E A = \frac{Δ L}{L} E A \to F = k \cdot A, essent σ = ε E, ε = \frac{Δ L}{L} . \\ (ε: deformació unitària, E: mòdul de Young o coeficient d’elasticitat i σ : és la tensió.) \end{matrix}

El signe negatiu de la llei de Hooke ens indica que F és una força recuperadora. També ens diu que F és directament proporcional a la distància de compressió o d’allargament de la molla (Δx).

El treball que cal fer per a desplaçar la molla entre dos punts és:

W = | - \int_{x_{1}}^{x_{2}} F dx | = | - \int_{x_{1}}^{x_{2}} k \cdot x dx | = | {[\frac{1}{2} {kx}^{2}]}_{x_{1}}^{x_{2}} | = \frac{1}{2} k Δ x^{2}

És a dir, que l’energia potencial acumulada per la molla en l’estat de màxima compressió o estirament és:

\begin{array}{c}{{E}_{p}=\frac{1}{2}k\mathrm{\Delta }{x}^{2}.}\end{array}

Robert Hooke presentà aquesta llei empírica el 1678.

2.2 Forces de fregament

Les superfícies manifesten una força de sentit oposat a la força que es fa sobre l’objecte amb el qual estàn en contacte. És la força de fricció, de poca intensitat, que és deguda als enllaços moleculars que es formen en les superfícies en contacte.

La força de fricció és proporcional a la força normal que fa una superfície sobre l’altra i no depèn de l’àrea de contacte perquè és proporcional a la força per unitat d’àrea. Per tant, la força màxima de fricció estàtica (força de fregament entre dos cossos que estan en repòs) és proporcional a la força normal entre les superfícies: $\displaystyle{{f}_{e,\mathit{m\grave{a}x}}⩽{\mu }_{e} \cdot N}$

El coeficient de fricció estàtica ${\mu }_{e}$depèn del material de construcció de les superfícies en contacte.

Però, quan el bloc està en moviment, els enllaços moleculars entre les superfícies es formen i es destrueixen contínuament. En aquest cas, la intensitat de la fricció cinètica (força de fregament d’un cos en moviment) depèn de la velocitat relativa entre les superfícies i de la seva naturalesa, és a dir, que el coeficient de fricció cinètic serà més petit que l’estàtic:

\begin{array}{c}{f}_{c}={\mu }_{c}N,{\mu }_{c}< {\mu }_{e}\end{array}

2.3 Forces fictícies o pseudo-forces

Les lleis de Newton sols són vàlides per a sistemes de referència inercials, és a dir, que es mouen amb velocitat uniforme. Quan un sistema de referència accelerat (no inercial) es mou respecte a un altre d’inercial, la força resultant no és la massa per l’acceleració$\mathrm{\Sigma }\vec{F}\ne m\cdot \vec{a}$

Però si introduïm en el sistema accelerat una força fictícia (que no és produïda per cap agent), $\displaystyle{\mathrm{\Sigma }\vec{F}=m\cdot \vec{a}}$ continuarà sent vàlid:$\vec{a}$ és l’acceleració relativa del sistema no inercial respecte a l’inercial. Un exemple de pseudoforça és la centrífuga que apareix en sistemes no inercials en rotació o la força de Coriolis.

Exemple:

Si es deixa caure un objecte dins d’un vagó que accelera (sistema no inercial) respecte a un observador en repòs que és a l’andana (sistema inercial), el que està en repòs veurà que cau verticalment amb l’acceleració de la gravetat, però el del vagó veurà que cau allunyant-se de la seva dreta. Com que l’única força que actua sobre l’objecte és la del pes, $\displaystyle{\vec{F}=m\cdot \vec{a}}$ no es compleix. No obstant això, si li apliquem una pseudoforça $\displaystyle{\vec{{F}_{s}}=-m\cdot \vec{a}}$, sí que es complirà.

L’acceleració d’una pseudoforça és igual a l’acceleració relativa del sistema en sentit contrari.

Les forces fictícies, inercials o d’Alembert, les presentà Jean Le Rond d’Alembert el 1743 en el Tractat de dinàmica. Les defineix com el producte negatiu de la massa per l’acceleració. No s’han de confondre amb les forces de reacció de la tercera llei de Newton.

3. Quantitat de moviment (moment lineal)

Una conseqüència important de la tercera llei de Newton és que, si no actua cap força que no sigui les d’acció i reacció entre dos objectes en contacte, la variació de la quantitat de moviment és nul·la. Com que la força que actua sobre cada objecte és d’igual magnitud, però de sentit contrari a la que actua sobre l’altre, la suma de les respectives quantitats de moviments es manté constant en el temps:

\begin{array}{c}{F}_{1}=\displaystyle{\frac{{\mathit{dp}}_{1}}{\mathit{dt}}}\text{ i }{F}_{2}=\frac{{\mathit{dp}}_{2}}{\mathit{dt}}\\[0.5cm] \text{Com que, }{F}_{1}=-{F}_{2},\displaystyle{\frac{{\mathit{dp}}_{1}}{\mathit{dt}}}=\frac{-{\mathit{dp}}_{2}}{\mathit{dt}}\text{ i }\frac{{\mathit{dp}}_{1}}{\mathit{dt}}+\frac{{\mathit{dp}}_{2}}{\mathit{dt}}=\frac{d}{\mathit{dt}}\left(\vec{{p}_{1}}+\vec{{p}_{2}}\right)=0\end{array}

Per tant, la llei de la conservació de la quantitat de moviment o moment lineal és:

\begin{array}{c}\vec{{p}_{1}}+\vec{{p}_{2}}=\mathit{constant}\end{array}

De fet, Isaac Newton formulà la tercera llei estudiant la quantitat de moviment abans i després del xoc de dos cossos. Si actuen forces que són molt més petites que les de contacte en el xoc (normalment un xoc és força violent) es poden menysprear i la llei continua complint-se.

Perquè aquesta llei pogués funcionar en forces a distància, la transmissió de la quantitat de moviment entre els dos cossos hauria de ser instantània, concepte que viola altres lleis físiques. La tercera llei i la de la conservació del moviment sols són aproximades per a dos cossos separats, però aquesta dificultat es resol mitjançant l’aplicació d’un camp gravitatori que transporta la quantitat de moviment a la velocitat de la llum.

Per a velocitats $v \geq 0,1 \cdot c$ la quantitat de moviment és $p’=\gamma \cdot m_0 \cdot v$

Definim l’impuls lineal com la força que actua durant un temps sobre una partícula. És la diferència de la quantitat de moviments entre dues posicions de la partícula:

\begin{array}\vec{I}=F\cdot \mathrm{\Delta }t=m\vec{{v}_{f}}-m\vec{{v}_{0}}\rightarrow \vec{I}=\mathrm{\Delta }p\end{array}

4. Dinàmica del moviment circular uniforme

La dinàmica rotacional estudia les causes de la cinètica rotacional o moviment circular.

Exemples:

Quina és la velocitat mínima en el punt més alt i en el punt més baix perquè el sistema estigui en equilibri?

En el punt més alt:

{\begin{matrix} T = P \\ P = F_{c} = \frac{m \cdot v^{2}}{R} \end{matrix} \to v = \sqrt{\frac{M \cdot g \cdot R}{m}}

En el punt més baix:

\begin{matrix} F_{c} = T + P \to \frac{m \cdot v^{2}}{R} = T + M \cdot g \\ Per a la velocitat mínima: \\ T = 0 \to v = \sqrt{\frac{MgR}{m}} \end{matrix}

Cinemàtica rotacional, pèndol punt més alt i punt mès baix

4.1 Moment d’una força

El moment d’una força («torque» en anglès, τ) del moviment rotacional és el concepte anàleg a la força $F$ del moviment translacional. Si apliquem una força $F$ sobre una partícula $P$ que és a una distància $R$ del punt de gir $O$ el moment de força $M$ crearà un moviment de rotació respecte a aquest punt (centre de rotació): ${M}=\vec{R}\times \vec{F}$ el mòdul del qual és: $M=F \cdot \sin \theta \cdot R=\mathit{F_y} \cdot R.$

$F_y$ és la força perpendicular al braç de palanca aplicada i $R$ és la distància des del punt d’aplicació fins al centre de rotació $O$ (braç de palanca). La força paral·lela al braç de palanca no la fa girar, sinó que tan sols l’estira o la comprimeix. És a dir, que les forces que passen pel centre de gir no creen moments de força $M$

El sentit del vector moment segueix la regla de la mà dreta i es calcula fent el determinant dels vectors radi i força. El producte vectorial no és commutatiu, per tant, s’ha de fer el determinant en l’odre indicat.

En el cas de dues forces paral·leles de sentit oposat es forma un parell de forces. Si les dues forces són de la mateixa magnitud però de sentit contrari: $M=2FR$.

4.2 Moment cinètic o angular

El moment cinètic o angular $\vec{L}$ de dinàmica rotacional és el concepte anàleg al moment lineal $\vec{p}$ de la dinàmica translacional. És un vector perpendicular al pla format pels vectors moment lineal $\displaystyle{\vec{p}}$ i radi $\displaystyle{\vec{R}}:$

\begin{array}\vec {L}=\vec {R} \times \vec {p}\end{array}

la magnitud del qual és:

\begin{matrix} L={R} \cdot {p} \sin(\theta).\end{matrix}

$p \cdot \sin \left( \theta \right)$ és la component perpendicular del moment lineal i $R$ el braç de palanca del moment. La component de la velocitat que travessi el centre de gir $O$ no contribuirà a la formació del moment cinètic.

Per tant,

\begin{matrix} \vec{R} \times \vec{F} = \frac{\vec{R} \times d \vec{p}}{dt} \to \vec{M} = \frac{\vec{R} \times d \vec{p}}{dt} \\ I, com que \\ \vec{L} = \vec{R} \times \vec{p} i \frac{d \vec{L}}{dt} = \frac{d}{dt} \vec{R} \times \vec{p} \to \frac{d \vec{L}}{dt} = \frac{d \vec{R}}{dt} \times \vec{p} + \vec{R} \times \frac{d \vec{p}}{dt} = (\vec{v} \times m \vec{v}) + \vec{R} \times \frac{d \vec{p}}{dt} \\ Ja que el producte vectorial de dos vectors paral·lels és zero: \\ \frac{d \vec{L}}{dt} = \vec{R} \times \frac{d \vec{p}}{dt} = \vec{R} \times \vec{F} \\ \vec{M} = \frac{d \vec{L}}{dt} \end{matrix}

És a dir, que la velocitat de canvi del moment cinètic d’una partícula és igual al moment de la força que hi actua. Que equival a les equacions escalars:

\begin{array}{c}\displaystyle{{M}{x}=\frac{d \vec{{L}_{x}}}{\mathit{dt}}\\{M}{y}=\frac{d\vec{{L}{y}}}{\mathit{dt}}\\{M}{z}=\frac{d\vec{{L}{z}}}{\mathit{dt}}}\end{array}

Aquest resultat és anàleg al del canvi de la quantitat del moviment:

\begin{array}{c}\displaystyle{{\vec{F}=\frac{d \vec{p}}{dt}}} \end{array} del moviment translacional.

Quan una força o moment extern constant fa variar $\vec{L}$ l’objecte en rotació fa un moviment de precessió.

4.3 Conservació del moment cinètic

Com que,

\begin{array}{c}\displaystyle{M=\frac{d\vec{L}}{\mathit{dt}}. \text{Si }M=0\text{, llavors, }\frac{d\vec{L}}{\mathit{dt}}=0}\end{array}

Per tant, si el moment de força extern que actua sobre una partícula és zero el moment cinètic roman invariable. Aquest és la llei de conservació del moment cinètic, anàleg a la de conservació del moment lineal.

5. Sistema de partícules

5.1 Centre de masses (CM)

Fins ara, hem fet suposicions per tal d’estudiar la dinàmica dels objectes com a partícules amb massa i sense dimensió, tant en el moviment de translació com en el de rotació. En el moviment de sistemes de partícules, cada partícula del sòlid o del sistema fa el mateix desplaçament en el mateix interval de temps.

Definim el ”centre de masses” d’un sòlid o d’un sistema de partícules com el punt que es mou de la mateixa manera que ho faria una única partícula.

\begin{matrix} En un sistema de dues partícules que es mouen per l’eix d’abcisses: \\ x_{cm} = \frac{m_{1} \cdot x_{1} + m_{2} \cdot x_{2}}{m_{1} + m_{2}} \to M \cdot x_{cm} = m_{1} \cdot x_{1} + m_{2} \cdot x_{2} \\ En conseqüència, en un sistema amb n partícules: \\ x_{cm} = \frac{m_{1} \cdot x_{1} + m_{2} \cdot x_{2} … m_{n} \cdot x_{n}}{m_{1} + m_{2} … m_{n}} \\ M \cdot x_{cm} = m_{1} \cdot x_{1} + m_{2} \cdot x_{2} … m_{n} \cdot x_{n} \\ \frac{\sum_{i = 1}^{n} m_{i} \cdot x_{i}}{\sum_{i = 1}^{n} m_{i}} \\ I, si el sistema de partícules es mou tridimensionalment: \\ x_{cm} = \frac{\sum_{i = 1}^{n} m_{i} \cdot x_{i}}{\sum_{i = 1}^{n} m_{i}}, y_{cm} = \frac{\sum_{i = 1}^{n} m_{i} \cdot y_{i}}{\sum_{i = 1}^{n} m_{i}}, z_{cm} = \frac{\sum_{i = 1}^{n} m_{i} \cdot z_{i}}{\sum_{i = 1}^{n} m_{i}} \\ En notació vectorial: \\ {\vec{r}}_{cm} = \frac{\sum_{i = 1}^{n} m_{i} \cdot \vec{r_{i}}}{\sum_{i = 1}^{n} M} \\ En un sòlid rígid, com que el sistema de partícules és tan gran, \\ si considerem que té una distribució contínua: \\ x_{cm} = \frac{\int x dm}{\int dm} = \frac{\int x dm}{M}, y_{cm} = \frac{\int y dm}{\int dm} = \frac{\int y dm}{M}, z_{cm} = \frac{\int z dm}{\int dm} = \frac{\int y dm}{M} \\ {\vec{r}}_{cm} = \frac{\int \vec{r} dm}{M} \end{matrix}

5.2 Moviment translacional del CM

Per a un sistema fix de partícules:

\begin{matrix} M {\vec{r}}_{cm} = m_{1} \vec{r_{1}} + m_{2} \vec{r_{2}} + … + m_{n} \vec{r_{n}} \\ \frac{d}{dt} (M {\vec{r}}_{cm}) = \frac{d}{dt} (m_{1} \vec{r_{1}} + m_{2} \vec{r_{2}} + … + m_{n} \vec{r_{n}}) \\ M {\vec{v}}_{cm} = m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}} + … + m_{n} \vec{v_{n}} \\ \frac{d}{dt} (M {\vec{v}}_{cm}) = \frac{d}{dt} (m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}} + … + m_{n} \vec{v_{n}}) \\ M {\vec{a}}_{cm} = m_{1} \vec{a_{1}} + m_{2} \vec{a_{2}} + … + m_{n} \vec{a_{n}} = \vec{F_{1}} + \vec{F_{2}} … \vec{F_{n}} \end{matrix}

Per tant,

\begin{array}\displaystyle{\vec M \cdot \vec{{a}_{cm}}=\mathrm{\Sigma }{\vec{F}_{externes}}}\end{array}

Les forces internes entre les partícules s’anul·len per la tercera llei de Newton i sols s’ha de tenir en compte les forces externes que actuen en el sòlid. És a dir, que el centre de masses del sistema de partícules es mou com si tota la massa i totes les forces estiguessin concentrades en aquest punt.

Per altra banda,

\begin{matrix} \vec{p} = M {\vec{v}}_{cm} \to M \frac{d \vec{p}}{dt} = M {\vec{a}}_{cm} = Σ {\vec{F}}_{externes} \\ i, si Σ {\vec{F}}_{externes} = 0 \to \frac{d \vec{p}}{dt} = 0 \end{matrix}

és a dir, que també es conserva la quantitat de moviment.

5.3 Moment cinètic i conservació M d’un sistema de partícules

El moment cinètic o angular d’un sistema de partícules respecte a un punt és:

\begin{matrix} \vec{L} = \vec{L_{1}} + \vec{L_{2}} + … \vec{L_{n}} = \sum_{i = 1}^{n} L_{i} \\ \frac{d \vec{L}}{dt} = {\vec{M}}_{externs} \end{matrix}

Com que, la suma de les forces internes entre les partícules és zero, la suma dels moments de força també ho serà.

5.4 Inèrcia rotacional i energia de rotació

Considerem un sistema discret de partícules que gira respecte a un eix fix d’un sistema de referència inercial (no accelerat). Cada partícula té una energia cinètica:

\begin{array}\displaystyle{{E}_{c}=\frac{1}{2}m{v}^{2}=\frac{1}{2}m{r}^{2}{w}^{2}}\end{array}

Si sumem l’energia de totes les partícules,

\begin{array}{c}\displaystyle{\mathrm{\Sigma }{E}_{c}=\frac{1}{2}\left({m}_{1}{r}_{1}^{2}+{m}_{2}{r}_{2}^{2}+\mathrm{…}+{m}_{n}{r}_{n}^{2}\right){w}^{2}\\ I=\sum\limits_ {i=1}^{n}{{m}_{i}{r}_{i}^{2}}\rightarrow {E}_{c}=\frac{1}{2}I{w}^{2}}\end{array}

La inèrcia rotacional $I$ d’un sòlid és la magnitud anàloga a la inèrcia translacional d’una massa$m$ És la resistència del sòlid a canviar el seu moviment de rotació.

Ara bé, per a un sòlid rígid (sòlid teòric indeformable), que podem considerar com un sistema continu i homogeni de matèria, el “teorema dels eixos paral·lels o de Steiner” diu que la relació entre la inèrcia rotacional d’un cos respecte a un eix que passa pel seu centre de masses i un eix paral·lel és: \begin{array}{c}\displaystyle{I={I}_{\mathit{cm}}+M{h}^{2}}\end{array}

Si considerem dos eixos de rotació perpendiculars al paper que passen pels punts ”CM” i ”P”:

la distància entre aquests dos eixos és ”h”
el quadrat de la distància des de la partícula $\displaystyle{m_i \text{ fins a CM és :} {x}_{i}^{2}+{y}_{i}^{2}}$
el quadrat de la distància entre $\displaystyle{m_i \text{ i } P \text{ és :} {\left({x}_{i}-a\right)}^{2}+{\left({y}_{i}-b\right)}^{2}}$

Per tant, el moment d’inèrcia de $m_i$ respecte a $P$ és:

\begin{matrix} I = Σ m_{i} {(x_{i} - a)}^{2} + {(y_{i} - b)}^{2} = Σ m_{i} (x_{i}^{2} + y_{i}^{2}) - 2 a Σ m_{i} x_{i} - 2 b Σ m_{i} y_{i} + (a^{2} + b^{2}) Σ m_{i} \\ I,  com que, Σ m_{i} \cdot x_{i} = Σ m_{i} \cdot y_{i} = 0, Σ m_{i} = M i Σ m_{i} (x_{i}^{2} + y_{i}^{2}) = I_{cm} (I  de m_{i} respecte  al  CM) \\ I = I_{cm} + M h^{2} \end{matrix}

Llavors, podem calcular i fer una taula amb els moments d’inèrcia respecte al CM de figures regulars per tal de calcular-lo respecte a un altre eix paral·lel usant el teorema anterior.

Exemple:

\begin{matrix} I_{cm} = \int_{R_{1}}^{R_{2}} r^{2} dm = \int_{R_{1}}^{R_{2}} r^{2} ρ 2 π r L dr = ρ 2 π L \int_{R_{1}}^{R_{2}} r^{3} dr \\ ρ 2 π L \frac{R_{2}^{4} - R_{1}^{4}}{4} = \frac{M}{π (R_{2}^{2} - R_{1}^{2}) L} 2 π L \frac{R_{2}^{4} - R_{1}^{4}}{4} = \frac{(R_{2}^{2} + R_{1}^{2}) \cdot (R_{2}^{2} - R_{1}^{2})}{2 (R_{2}^{2} - R_{1}^{2})} M \\ I_{cm} = \frac{(R_{2}^{2} + R_{1}^{2})}{2} M \\ 2. Calculem I respecte a un eix paral·lel: \\ I = I_{cm} + {Mh}^{2} \end{matrix}

5.5 Dinàmica d’un sòlid rígid

Per a cada partícula del sòlid rígid es compleix que:

\begin{matrix} M = R \cdot F \sin (θ) \\ I com que: ds = R \cdot d θ \\ dW = \vec{F} \cdot d \vec{s} = F \cdot \sin θ \cdot ds = F \sin θ \cdot R d θ \\ Per tant: \\ dW = M \cdot d θ \\ \frac{dW}{dt} = M \frac{d θ}{dt} \\ En conseqüència: \\ P = Mw \end{matrix}

Per tant, el treball fet i la potència per a totes les partícules del sòlid és:

\begin{matrix} dW = F_{1} \cos ϕ_{1} r_{1} d θ + F_{2} \cos ϕ_{2} r_{2} d θ + … + F_{n} \cos ϕ_{n} r_{n} d θ \\ (M_{1} + M_{2} + … + M_{n}) d θ = M_{extern} d θ \\ \frac{dW}{dt} = M_{extern} \frac{d θ}{dt} \to P = M_{extern} w \\ I la velocitat de canvi de l'energia cinètica del sòlid és: \\ \frac{d}{dt} (\frac{1}{2} {Iw}^{2}) = Iw \frac{dw}{dt} = I \cdot w \cdot α \\ I com que: Mw = I \cdot w \cdot α \\ M = I α \end{matrix}

Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?

Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.

Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons

Inequacions

Instruccions abans de començar

1. Definició:

Una inequació és una expressió algebraica que en relaciona els dos termes amb una desigualtat ($<, \leq, >, \geq$).

La solució d’una equació real és sempre un o més nombres reals. En canvi, la solució d’una inequació en una dimensió és un o més intervals i en dues una regió.

La resolució d’una equació o d’un sistema d’inequacions varia segons el grau i el nombre d’incògnites de l’equació o sistema. No obstant això, el procediment per a resoldre una inequació és el mateix que per a resoldre una equació, però canviem el sentit de la desigualtat quan la incògnita que aïllem perd el signe.

El mètode general per a resoldre una inequació és:

1. Si n’hi ha, eliminem els denominadors de la inequació.

2. Si n’hi ha, desfem els parèntesis aplicant la propietat distributiva.

3. Agrupem els monomis semblants.

4. Resolem l’equació obtinguda.

5. Si cal, invertim el sentit de la desigualtat.

6. Fem la representació el resultat sobre la recta real (una variable) o en sistema de cartesianes (dues variables) i determinem quina és la solució tenint en compte si els extrems o la regió són oberts/a o tancats/a (si la desigualtat conté un signe =, seran tancats, sinó, seran oberts). La solució de la inequació també es pot indicar en forma algebraica o d’interval (una variable).

2. Tipus d’inequacions

2.1 De primer grau

2.1.1 D’una variable

Les resolem com si fos una equació de primer grau tenint en compte el guió anterior. La solució serà un interval sobre la recta real, que es dividirà en nombre_ de_solucions+1 intervals.

Exemple:

$
\displaylines{
\frac{3x+3}{4}<=\frac{5(x+1)}{2}
\\3x+3<=2 \cdot {(5x+5)}
\\3x+3<=10x+10
\\3x-10x<=10-3
\\-7x<=7
\\x>=\frac{7}{-7}
\\x>=1
}
$

La representació gràfica d’aquesta solució és l’interval de la recta real:

I les solucions en forma algebraica i d’interval són: $x>=1, [1, +\infty)$.

2.1.2 De dues variables

Per a determinar quin és el semiplà solució, calcularem si el punt de mostra (0,0) -agafem aquest punt per facilitat de càlcul- compleix o no la inequació. Si la compleix, la regió solució serà el semiplà que el conté, si no, ho serà l’altre.

$
y \leq 2x+3\\
0 \leq 2 \cdot 0+3\\
0 \leq 3\\
$

Per tant, el semiplà de la dreta és la regió solució de la inequació.

2.2 De segon grau

2.2.1 D’una variable

Seguim el guió de resolució d’inequacions, però ara haurem de resoldre una equació de segon grau.

Exemple:

$ \displaystyle{ \frac{10x^2-7}{3}=3x^2+6\\ 10x^2-7=9x^2+18\\ x^2=25\\ x\pm \sqrt{25}\\ x\pm 5 } $

La representació gràfica és:

Ara, agafem un punt de cada interval (-10, 0, +10, per exemple) i l’introduïm a la inequació per a comprovar si se’n compleix la desigualtat:

Per tant, la solució és l’interval $-5 \leq x \leq +5, \text{o bé }, (-5,+5)$.

Exemple:

Determineu els intervals que són solució de la següent inequacioó:

$\displaystyle{\frac{x^2-7x+10}{x^2-9}<0}$

Seguim el guió de resolució i determinem el signe de cada interval per a cadascuna de les inequacions substituint un valor de l’interval en cada inequació. A continuació, el determinem per al quocient d’ambdues inequacions en els intervals formats entre dos extrems consecutius. La solució seran els intervals on el quocient tingui signe negatiu.

Per tant, la solució és: (-3,+2]U(+3,+5).

3. Sistemes d’inequacions

Per a determinar la regió (R) solució d’un sistema d’inequacions resoldrem cada inequació i després trobarem la que sigui comuna a ambdues.

3.1 D’una variable

Resolem cada inequació com en l’apartat 2.1. La solució és l’interval comú de les dues inequacions. Cal determinar si els extrems són oberts o tancats.

Exemple:

$$
\begin {cases}
3x+4 \leq 2x+10\\
2x-3 >-5
\end {cases}
\\[1cm]
x+4 \leq 2x+10 \rightarrow 3x-2x \leq 10-4 \rightarrow x \leq 6 \\
2x-3>-5 \rightarrow 2x>+3-5 \rightarrow x<-{\frac{2}{2}} \rightarrow x<-1 $$

Exemple:

$$
\begin {cases}
2x+5 \geq 2-x \\
2x^2-2x-2 \leq x^2-x+4
\end {cases}
\\
\begin {cases}
2x+x \geq 2-5 \\
2x^2-x^2-2x+x-2-4 \leq 0
\end {cases}
\\
\begin {cases}
3x\geq -3 \\
x^2-x-6 \leq 0
\end {cases}
\\
\begin {cases}
x\geq -1 \\
x \leq 3,-2
\end {cases}
$$

En aquest cas, representem gràficament cada inequació i determinem la regió de solució:

Per tant, l’interval solució és $-2 \leq x \leq -1, [-2,-1]$.

3.2 De dues variables

(Vegeu l’apartat 3. de l’entrada Programació lineal)

Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?

Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.

Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons

Teoria redox

Instruccions abans de començar

1. Introducció

Inicialment, s’anomenava oxidació a la reacció d’una substància amb l’oxigen i reducció a la pèrdua d’oxigen. Més endavant, es va generalitzar el concepte per a reaccions en les quals no intervenia l’oxigen i es va anomenar oxidació a la pèrdua d’electrons i reducció al guany d’electrons d’una substància.

Els compostos que oxiden a altres substàncies es redueixen i els que les redueixen s’oxiden. Els primers són agents oxidants i els segons reductors. Tot i que les reaccions d’oxidació s’associen a la formació d’òxids, hi ha més espècies químiques que poden fer d’oxidants.

En una reacció d’oxidació-reducció (redox) canvia el nombre d’oxidació d’algunes de les espècies químiques involucrades. És, per tant, una reacció amb transferència d’electrons.

1.1 Nombre d’oxidació i valència:

1.1.1 Nombre d’oxidació:

L’estat o nombre d’oxidació d’un àtom és la càrrega hipotètica que tindria si tots els enllaços que forma fossin totalment iònics. Determina el grau d’oxidació o de pèrdua d’electrons d’un àtom. Pot ser positiu, negatiu o zero, però no és la càrrega real de l’àtom, sinó una manera d’entendre la nomenclatura inorgànica i algunes reaccions químiques.

A nomenclatura orgànica es representa amb un nombre romà que es col·loca després de l’element entre parèntesis.

(El nombre d’oxidació o estat d’oxidació d’un element és la propietat d’un àtom en un compost que mesura el grau de control que té sobre els electrons seus comparat amb els d’aquest element en estat pur. Representa la càrrega que tindria un àtom si tots els enllaços que té amb la resta d’àtoms del compost fossin plenament iònics – no hi ha enllaços plenament iònics, tot i que alguns ho són molt. Per tant, no és la càrrega real d’un àtom. La causa són els petits desplaçaments que fan els electrons en funció de la diferència d’electronegativitat dels àtoms que formen el compost. Varia segons l’escala d’electronegativitat usada per a calcular-la.)

El descrivim amb un valor numèric amb signe que indica el canvi del nombre d’electrons controlats. Per exemple, que el nombre d’oxidació de l’oxigen sigui -2 vol dir que ha guanyat el control de dos electrons addicionals. El nombre d’oxidació s’empra tant en la nomenclatura orgànica com en la inorgànica.

1.1.2 València:

La valència d’un element representa la capacitat de combinació que té quan forma compostos químics o molècules amb altres àtoms. La determina el nombre d’àtoms d’hidrogen (o d’enllaços simples) amb els quals es pot combinar l’element. Per exemple, en el metà la valència del carboni és quatre, en l’amoníac la valència del nitrogen és tres i en l’aigua la valència de l’oxigen és dos. En el $PCl_5$, la del fòsfor és cinc i la del clorur 1.

En les substàncies iòniques la valència és la càrrega iònica mentre que en els covalents indica el nombre d’enllaços formats (CO₂: valència C és 4, valència O és 2).

1.2 Parell redox i semireaccions:

1.2.1 Parell redox:

A l’agent reductor i l’agent oxidant d’una reacció d’oxidació-reducció se l’anomena parell redox. Com més forta sigui la forma oxidant, més feble serà la reductora i a l’inrevés.

$
\displaystyle{
\begin{matrix}
Fe^{+3} + 1e^{-} &⇌& Fe^{+2 }\\
\text{Agent oxidant} &⇌& \text{Agent reductor} \\
\text{(Es redueix)} &⇌& \text{(S’oxida)}
\end{matrix}
}
$

La taula de potencials estàndard de reducció (25ºC, 1 atm) és un arranjament dels potencials estàndard de reducció de parells redox relatius a un elèctrode d’hidrogen.

L’elèctrode estàndard d’hidrogen és la base de l’escala termodinàmica dels potencials d’oxidació-reducció. Té un potencial absolut de $4,44 \pm 0,02 V$ a 25 °C, però li assignem el valor zero a qualsevol temperatura quan el comparem amb el potencial d’altres reaccions per tal d’obtenir la taula de potencials estàndard de reducció.

El potencial de reducció (Eº, volts) és una mesura de la capacitat reductora d’un element o compost.

(Segons la IUPAC, és el valor de la força electromotriu d’una cel·la en la qual l’hidrogen molecular ($H_2$) a pressió estàndard s’oxida a ions solvatats ($H_3O^+$) a l’elèctrode de l’esquerra. Si el dissolvent és l’aigua, a la solvatació l’anomenen hidratació. La solvatació és el fenomen que es produeix en una dissolució que consisteix en l’atracció de les molècules de dissolvents i els ions/molècules de solut).

1.2.2 Semireaccions

A cadascuna de les reaccions d’oxidació i de reducció d’una reacció redox global en una cel·la galvànica o electrolítica se l’anomena semireacció. Les semireaccions d’una reacció redox es determinen observant els canvis del nombre d’oxidació de les substàncies involucrades en la reacció.

$
H^{+1}N^{ \color {red} {+5}} O_3^{-2} + H^{+1}I^{\color {red}{-1}} → N^{\color {red}{+2}}O^{-2} + I_2^{\color {red}{0}} + H_2^{+1} O^{-2}
$

La semireacció d’oxidació es produeix sempre a l’ànode i la de reducció al càtode. No obstant això, en les cel·les galvàniques l’ànode és negatiu i el càtode positiu i en les electrolítiques l’ànode és positiu i el càtode negatiu. Les usem per a fer els balanços de matèria i elèctrics d’una reacció.

$Zn^{0} – 2e^{-} \rightarrow Zn^{+2} \enspace \text{E⁰=0,76 v}
\\
Cu^{+2} + 2e^{-} \rightarrow Cu^{0} \enspace \, \text{E⁰=0,34 v}
\\
\text{——————————————}
\\
Zn^{0} + Cu^{+2} \rightarrow Zn^{+2} + Cu^{0} \enspace \text{E⁰=1,10 v}
$

Una reacció espontània (E⁰>0) produeix un potencial a la cel·la E⁰ (cel·la)= E⁰ (càtode) – E⁰ (ànode). E⁰ (ànode) i E⁰ (càtode) són els valors de taula de potencials estàndard de reducció per a cada semireacció. Si la reacció és espontània, l’energia lliure de Gibbs ha de ser negativa: $\Delta G_{cel·la}=-n \cdot F \cdot E⁰_{cel·la}.$

2. Ajust reaccions redox. Mètode ió-electró

El balanç d’equacions redox es fa primer fent l’ajust màssic de cada semireacció i després l’electrònic. Per a ajustar els hidrògens i oxígens de la semireacció: a) si es produeix en medi àcid, afegirem al terme deficitari en oxígens tantes molècules d’aigua com deficiència d’oxígens tingui i els ions H⁺ que calguin a l’altra, b) si es produeix en medi bàsic, afegirem el doble d’OH^– al deficitari en oxigen i les mateixes molècules d’aigua a l’altra:

2.1. En medi àcid

\(
\displaystyle{
1. \text{Esbrinem quines són les espècies químiques en els quals varia el nombre d’oxidació:}
\\[0.5cm]
K_2^{+1}(Cr_2^{\color {red} {+6}} O^{-2}_7) + Fe^{\color {red} {+2}}(S^{+6}O^{-2}_4) + H^{+1}_2(S^{+6}O^{-2}_4) \rightarrow Cr^{\color {red} {+3}}_2 (S^{+6}O^{-2}_4)_3 + Fe^{\color {red} {+3}}_2 (S^{+6}O^{-2}_4)_3
\\[0.5cm]
2. \text{Escrivim les semireaccions:}
\\[0.5cm]
(Cr_2^{\color {red} {+6}} O^{-2}_7) \rightarrow Cr^{\color {red} {+3}}
\\[0.5cm]
Fe^{ \color {red} {+2}} \rightarrow Fe^{\color {red} {+3}}
\\[0.5cm]
3. \text{Fem el balanç màsic de cada semireacció. :}
\\[0.5cm]
(Cr_2^{\color {red} {+6}} O^{-2}_7) + 14 H^+ \rightarrow 2 Cr^{\color {red} {+3 }} + 7 H_2 O
\\[0.5cm]
\text{(escriurem els grups químics, els gasos i els precipitats sencers i no tan sols els elements}
\\
\text{d’aquests que s’oxiden o es redueixen.)}
\\[0.5cm]
\text{( Després d’ajustar els àtoms de crom hi afegim set molècules d’aigua per a ajustar l’oxigen}
\\[0.5cm]
\text{i } 14H^+\text{ per a ajustar els ions hidrogen).}
\\[0.5cm]
Fe^{ \color {red} {+2 }} \rightarrow Fe^{\color {red} {+3 }}
\\[0.5cm]
\text{( No cal ajustar els àtoms de ferro ).}
\\[0.5cm]
4. \text{Fem el balanç electrònic:}
\\[0.5cm]
(Cr_2 O_7)^{-2}+ 14H^{+} + \color {red} {6e^{-}} \rightarrow 2 Cr^{+3 } + 7 H_2 O
\\
\color {red} {+12} \rightarrow \color {red}{+6}
\\[0.5cm]
Fe^{+2 } -\color {red} {1e^{-}}\rightarrow Fe^{+3 }
\\
\color {red} {+2} \rightarrow \color {red}{+3}
\\[0.5cm]
\text{Multipliquem la semireacció del ferro per sis per a igualar els electrons que es produeixen i els que es }
\\
\text{consumeixen i escrivim la reacció iònica global:}
\\[0.5cm]
(Cr_2 O_7)^{-2} + 14H^{+} + 6e^{-}\rightarrow 2 Cr^{+3 } + 7 H_2 O \\
6 Fe^{+2 } -6e^{-} \rightarrow 6Fe^{+3 }
\\
\text{_________________________________________________}
\$Cr_2 O_7)^{-2} + 14H^{+} + 6 Fe^{+2 } \rightarrow 2 Cr^{+3 } + 7 H_2 O +6Fe^{+3 }
\\[0.5cm]
6.\text{Escrivim la reacció molecular global:}
\\[0.5cm]
K_2 \color {red}{(Cr_2 O_7)}+ \color {red} {6 Fe}(SO_4) + \color {red} {7H_2}(SO_4) \rightarrow \color {red} {Cr_2}(SO_4)_3 + \color {red} {7H_2 O} + \color {red} {3Fe_2}(SO_4)_3 + K_2( SO_4 )
\\[0.5cm]
\text{(El potassi no intervé en les semireaccions, tanmateix, també és part de la reacció global ).}
\\[0.5cm]
}
$

2.2. En medi bàsic

\(
\displaystyle{
K(MnO_4) + NH_3(g) → K(NO_3) + MnO_2 \downarrow + K(OH)
\\[0.5cm]
\text{Per a fer l’ajust en medi bàsic seguirem el mateix procediment que abans:}
\\[0.5cm]
1. K^{+1} Mn^{\color {red}{+7}}O_4 ^{-2} + N^{\color {red}{+3}}H_3 ^{-1} → K^{+1} N^{\color {red}{+5}} O_3^{-2} + Mn^{\color {red}{+4}}O_2^{-2} \downarrow + K^{+1} O^{-2} H^{+1}
\\[0.5cm]
2.
\\[0.5cm]
( MnO_4 )^{ – } \rightarrow MnO_2 \downarrow
\\[0.5cm]
NH_3( g ) \rightarrow ( NO_3 )^{ – }
\\[0.5cm]
3.
\\[0.5cm]
( MnO_4 )^{-} + {\color {red}{2H_2O}}\rightarrow MnO_2 \downarrow + {\color {red}{4OH^{-}}} \enspace(a)
\\[0.5cm]
NH_3( g ) + {\color {red}{9OH^{-}}} \rightarrow ( NO_3 )^{ – } + {\color {red}{6H_2 O}} \enspace(b)
\\[0.5cm]
\text{a. Per a ajustar l’oxigen, en el membre que n’hi hagi en excés hi afegim les molècules}
\\
\text{d’aigua que continguin el mateix nombre d’àtoms. A continuació, afegim el doble } d’OH^{-}
\\
\text{que molècules d’aigua en el membre que tingui defecte d’oxígen.}
\\[0.5cm]
\text{b. Si cal ajustar els hidrogen, on n’hi hagi defecte i afegim tantes molècules d’aigua }
\\
\text{com àtoms hi manquin. Afegim a l’altra banda el mateix nombre } d’OH^{-}.
\\[0.5cm]
\text{En el cas de la semireacció de l’amoníac, l’ajustament dels hidrògens s’afegirà al }
\\\text{dels oxigens.}
\\[0.5cm]
4.
\\[0.5cm]
( MnO_4 )^{ – } + {2H_2 O}^0 + {\color {red}3e^-}\rightarrow MnO_2^0 \downarrow + {4OH^{- }}
\\[0.5cm]
NH_3^0( g ) + {9OH^{-}} – {\color {red}8e^{-}}\rightarrow ( NO_3 )^{ – } + {6H_2 O}^0
\\[0.5cm]
5.
\\[0.5cm]
{\color {red} 8} \cdot ( MnO_4 )^{ – } + {2H_2 O}^0 + {\color {red}3e^{-}}\rightarrow MnO_2^0 \downarrow + 4OH^{- }
\\[0.5cm]
{\color {red} 3} \cdot NH_3^0( g ) + {9OH^{-}} – {\color {red}8e^{-}}\rightarrow ( NO_3 )^{ – } + {6H_2 O}^0
\\[0.5cm]
\text{_________________________________________________}
\\[0.5cm]
8( MnO_4 )^{ – } + 3NH_3( g ) \rightarrow 8MnO_2 \downarrow + 3( NO_3 )^{ – } + 2H_2 O + 5OH^{-}
\\[0.5cm]
6
\\[0.5cm]
8K( MnO_4 ) + 3NH_3( g ) \rightarrow 8MnO_2 \downarrow +
3K( NO_3 ) + {2H_2 O} + 5KOH_3 ) + {2H_2 O} + 5KOH
}
\)

3. Cel·les galvàniques o voltaiques (piles) i electrolítiques

3.1 Piles

És un dispositiu en el qual dues barres de metall (elèctrodes) que estan en contacte mitjançant un electròlit en cada cel·la generen una diferència de potencial a causa de les reaccions que es produeixen en la superfície del metall.

En un dels elèctrodes el metall es dissol (fins que la càrrega és prou elevada per evitar més ionitzacions) i es genera una diferència de potencial entre la barra de metall i la dissolució (potencial de la semicel·la). Aquest elèctrode, en el qual es produeix l’oxidació, és l’ànode, i té càrrega negativa a causa de la fugida d’electrons per la barra.

En l’altre elèctrode, els ions de la dissolució electrolítica agafen aquests electrons i s’hi dipositen. Per tant, la barra tindrà càrrega positiva. Aquest elèctrode, en el qual es produeix la reducció, és el càtode.

Ambdós elèctrodes es connecten amb una dissolució iònica (pont salí) amb els extrems tapats amb cotó fluix o amb una membrana porosa per tal de permetre la mobilitat dels ions sense que passin a les dissolucions.

La reacció global en una pila és una reacció espontània, és a dir, que no li cal energia externa perquè es produeixi.

Exemple:

$
\displaystyle{
Zn^{0}(s) – 2e^{-} \rightarrow Zn^{+2} \text{(oxidació-ànode)} \\
Cu^{+2} + 2e^{-} \rightarrow Cu^{0} \text{(reducció-càtode)}\\
\text{________________________________________} \\
Zn^{0}(s)+ Cu^{+2} \rightarrow Zn^{+2} + Cu^{0}\text{(reacció global)}
}
$

La nomenclatura estàndard per aquesta una pila és:

$Zn^0(s)/Zn^{+2}(M) || Cu^{+2}(M)/Cu^0$

Una pila pot ser primària si no és reversible o secundària si es pot recarregar (reversible) amb corrent. Si l’electròlit és una pasta, diem que és una pila seca.

3.2 Electrolítiques

Una cel·la electrolítica és una cel·la en la qual es produeix el fenomen de l’electròlisi. L’electròlisi és la producció forçada (no espontània) d’una reacció química fent passar un corrent a través d’un electròlit (líquid format per ions positius i negatius que deixa passar l’electricitat).

El corrent elèctric genera sobre els elèctrodes les reaccions d’oxidació i reducció. El voltatge mínim necessari perquè es produeixi la descomposició és anomenat potencial de descomposició. Els cations van al càtode (-) i els anions a l’ànode (+). Ara, a diferència de les piles, l’ànode és positiu perquè està connectat al terminal positiu de la bateria i el càtode és negatiu.

3.2.1 Electròlisi de l’aigua

$
\begin{matrix}
2H_2 O(l) &-& 4e^{-} & \rightarrow & O_2 ( g) +4 H^{+} (aq) \hspace{2cm}E^0\text{=-1,229v( Oxidació-Ànode )} \\
4H^{ + } &+& 4e^{ – } & \rightarrow & \enspace2H_2 ( g ) \hspace{3.2cm} E^0\text{=0v ( Reducció-Càtode )}
\end{matrix}
\\
\text{_________________________________________________________________________}
\\
2H_2 O \rightarrow O_2 (g) + 2H_2 ( g ) \hspace{5.4cm}E⁰\text{( cel·la)=-1,229V}
$

És el procés de separació de l’aigua en gas oxigen i gas hidrogen mitjançant electròlisi. Com que l’aigua pura no té prou ions lliures per a conduir el corrent, s’acidifica amb sulfúric per tal d’augmentar la concentració d’ions hidrogen H⁺.

L’àcid sulfúric no es consumeix, i el volum d’hidrogen produït és el doble que el d’oxigen. S’ha d’aplicar una diferència de potencial mínima d’1,229 V perquè es produeixi la descomposició de l’aigua.

El gas d’hidrogen va al càtode (-) i el gas d’oxigen (+) a l’ànode.

3.2.2 Lleis de Faraday

Les dues lleis de Faraday de l’electròlisi són:

1. La massa d’un element que es diposita en un elèctrode és directament proporcional a la càrrega elèctrica que hi circula.

2. Per a fer circular 1 mol d’electrons calen 96 500 C (constant de Faraday):

Exemple:

Una cel·la electrolítica que conté una sal d’argent es connecta en sèrie amb una altra que en conté una de ferro. Si hi circula un corrent de 5 A durant cinc minuts, calculeu la massa dipositada de cada element.

(Una de les aplicacions més importants de l’electròlisi és la fabricació de peces amb recobriments metàl·lics.)

$
\displaystyle{
\small{
1. \text{Escrivim les semireaccions de reducció per a cada element}
\\[0.5cm]
Ag(aq) + 1e^{- } \rightarrow Ag^0 ( s )
\\[0.5cm]
Fe^{+3} (aq) + 3e^{-} \rightarrow Fe^0 ( s )
\\[0.5cm]
2. \text{Calculem la càrrega elèctrica que circula per a cada cel·la en cinc minuts:}
\\[0.5cm]
Q= I \cdot t= 5 A \cdot ({5 min} \cdot {\frac{60 s} {1 min }})=1 500 C
\\[0.5cm]
3. \text{Per tant, la massa dipositada de cada element és:}
\\[0.5cm]
m_{Ag}=1 500C \cdot {\frac{\text{1 mol } e^{-}}{ 96500C }} \cdot {\frac{107,87g Ag} { \text {1 mol } e^{-}}}=0,0155g
\\[0.5cm]
m_{Fe}=1 500C \cdot {\frac{\text{1 mol }e^{-}} { 96500C }}\cdot {\frac{\text{1 mol Fe }} { \text{3 mol } e^{-} }}\cdot {\frac{55,85g Fe}{\text{1 mol Fe}}}=0,289g
}
}
$

Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?

Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.

Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons

Equilibri de les reaccions de precipitació

Instruccions abans de començar

1. Definicions

Solut: substància que es dissol en un dissolvent formant una dissolució.

Dissolvent: substància que dissol altres substàncies formant una dissolució.

Dissolució: Mescla o barreja homogènia d’un component que en dissol un altre. Al component majoritari de la mescla l’anomenem dissolvent i al minoritari solut. El dissolvent més habitual és l’aigua.

En dissoldre’s un solut, se separen les parts de les quals està format. Sol haver-hi solvatació (interacció entre les molècules del solut i del dissolvent).

Dissolució saturada: dissolució que té la màxima quantitat possible de solut (substància que es dissol en un dissolvent formant una dissolució) dissolta a una temperatura determinada. En una dissolució saturada, la substància no dissolta (precipitat) està en equilibri amb la dissolta. Per tant, la velocitat amb la qual les partícules dissoltes formen el precipitat és la mateixa que la de les partícules que es dissolen.

Dissolució insaturada: dissolució que té menys quantitat de solut que la que s’ha de menester per tal d’arribar a l’equilibri anterior.

Dissolució sobresaturada: dissolució que té més quantitat de solut que la que cal per tal d’arribar a l’equilibri anterior. Les solucions sobresaturades també es poden formar refredant molt lentament una dissolució saturada.

Aquestes dissolucions són metaestables i, en conseqüència, quan s’hi afegeix un nucli cristal·lí cristal·litza l’excés de solut — metaestabilitat: condició d’un sistema l’estabilitat del qual es pot alterar fàcilment, de tal manera que una petita pertorbació farà que passi a un estat amb menys energia.

(Vegeu l’entrada Mescles i Barreges per a saber-ne més)

Solubilitat: Proporció de solut que es dissol en un dissolvent per a formar una solució saturada. La solubilitat d’un sòlid en un líquid augmenta amb la temperatura, però la d’un gas minva.

Depèn de la temperatura, de la pressió, de la subdivisió del solut i de la naturalesa del solut i del dissolvent, però, per als sòlids, l’efecte de la pressió és molt petit.

En augmentar la temperatura, la solubilitat augmenta si la dissolució és endotèrmica (el cas més habitual), tanmateix, disminueix si és exotèrmica.

Constant del producte de solubilitat (Kps): és el producte de les concentracions dels ions d’un compost en una dissolució saturada. Representa la constant d’equilibri de la dissolució de sals poc solubles.

$
\displaystyle{
A_x B_y(s) ⇌ x A^{+y} + y B^{-x}
\\[0.5cm]
K_e=\frac{ [A^{+y}]^x \cdot[B^{-x}]^{y } }{AB(s) }
}
$

Com que la concentració d’un sòlid no dissolt és u,

$ K_{ps}=[A^{+y}]^x [B^{-x}]^y$

Producte iònic (Q): és el producte de les concentracions dels ions d’un compost en una dissolució saturada.

Si el producte iònic (Q) és més gran que el producte de solubilitat (Kps), hi ha precipitació (dissolució sobresaturada). Si és més petit, la dissolució és insaturada. Si Q=Kps, la dissolució és saturada (dissolució tèrbola, a punt de precipitar).

(Vegeu l’entrada Equilibri químic per a saber-ne més)

2. Càlcul de la solubilitat:

Quan la dissolució està saturada, encara no ha començat a precipitar i la concentració dels ions és la solubilitat (s) del compost. Per tant,

$\displaystyle{
\begin{matrix}
AB & ⇌ & x A^{+y}+ & + & y B^{-x} \\ M & ⇌ & 0 & + & 0 \\ M-s& ⇌ & x.s & + & y.s
\end{matrix}
\\[0.5cm]
K_{ps}=[A^{+y}]^x [B^{-x}]^y=[xs]^x [ys]^y
}
$

Exemple:

$
\displaystyle{
\begin{matrix}
& Mg (OH)_2(l) & ⇌ & Mg^{++}_{(l)} & + & 2 (OH)^{-I}_{(1)} \\
\text{Concentracions inicials} & M & & 0 & & 0 \\
\text{Concentracions en equilibri} & M-s & &s & & 2s \\
\end{matrix}
}
$

Per tant,

$
\displaystyle{
K_{ps}=[Mg^{++}_{(l)}] [OH^-]^2=s.(2s)^2=4s^3→s=\sqrt[3] {\frac{K_{ps}} {4}}
}
$

Tenint en compte la relació dels elements del compost, el producte de solubilitat és:

$
A_x B_y ⇌ [ A^{+y} ]^x [ B^{-x} ]^y=(xs)^x \cdot (ys)^y
\\[0.5cm]
AB \,(x=1,y=1) \rightarrow K_s=[ A^{+} ] [ B^{-} ]=s^2 \rightarrow s=\sqrt{ K_{ps}}
\\[0.5cm]
A_2 B \,(x=2,y=1) \rightarrow K_s=[ A^{+} ]^2 [ B^{-2} ]=4s³ \rightarrow s=\sqrt [3]{ K_{ps} \div 4 }
\\[0.5cm]
A B_2 \, (x=1, y=2) \rightarrow K_s=[ A^{++} ] [ B^{-} ]²=4s^3 \rightarrow s=\sqrt[3]{ K_{ps} \div 4}
\\[0.5cm]
A_3 B \, (x=3, y=1)\rightarrow K_s=[ A^{+} ]³[ B^{-3} ]=27s^4 \rightarrow s=\sqrt[4] {K_{ps}\div 27}
\\[0.5cm]
A B_3 \, (x=1, y=3)\rightarrow K_s=[ A^{+3} ] [ B^{-} ]³=27s^4 \rightarrow s=\sqrt[4] {K_{ps}\div 27}
\\[0.5cm]
A_3 B_2 \, (x=3, y=2)\rightarrow K_s=[ A^{+2} ]³ [ B^{-3} ]²=108s^5 \rightarrow s=\sqrt[5] {K_{ps}\div 108}
\\[0.5cm]
etc.
$

Segons la llei de Le Chatêlier, la solubilitat minvarà per l’efecte de l’ió comú i augmentarà si s’hi afegeix aigua, ions que formin substàncies insolubles, ions complexos o que eliminin algun dels productes de la reacció.

2.1 Corbes de solubilitat

Les corbes de solubilitat representen gràficament la solubilitat d’una substància en un dissolvent, que normalment és aigua.

La solubilitat es mesura en grams de la substància dissolta per cada 100 grams d’aigua.

3. Precipitació fraccionada:

És un mètode químic de separació de dos o més ions en dissolució que precipiten per l’addició d’un ió comú. La solubilitat de les substàncies formades ha de ser prou diferent per tal que la separació sigui bona i esglaonada.

Precipitarà primer la substància que hagi de menester menys concentració de l’ió comú afegit, però abans de fer-ho completament començarà a precipitar la segona i, per tant, en aquest moment ambdues precipitaran al mateix temps. En aquest punt, les concentracions dels ions de la dissolució són en un equilibri controlat pels productes de solubilitat ($K_{ps}$) respectius.

Exemples:

A una dissolució de cromat de potassi 0,1 M i de clorur de sodi 0,05 M s’hi afegeix nitrat d’argent. Suposant que el volum no varia, quina sal precipitarà primer? Calculeu la concentració de l’anió de la sal que precipita primer quan comenci a precipitar la segona.

\(
\displaystyle{
K_{ps}( K_2 CrO_4 )=2,0.10^{-12}, \, K_{ps}( AgCl )=1,7.10^{-10}
\\[0.5cm]
\text{Abans de la precipitació, la concentració dels ions en dissolució és:}
\\[0.5cm]
\begin {matrix}
K_2 CrO_4 & \rightarrow & 2K^{+} &+& CrO_4^{-2} \\
0 &\rightarrow & 2 \cdot 0,1 &+& 0,1
\end {matrix}
\\[0.5cm]
\begin {matrix}
NaCl &\rightarrow & Na^{+} &+& Cl^{-} \\
0 &\rightarrow& 0,05 & + & 0,05
\end {matrix}
\\[1cm]
\text{Les reaccions de precipitació que es produiran són:}
\\[1cm]
\begin{matrix}
2Ag^+ &+& CrO^{-2}_{4} &⇌& Ag_2(CrO_4) \downarrow \\
Ag^+ &+& Cl^{-} &⇌& AgCl \downarrow
\end {matrix}
\\[1cm]
\text{1. La } [ Ag^{+} ] \text{ perquè precipiti cada substància és:}
\\[0.5cm]
[ Ag^{+} ]=\sqrt{\frac{K_{ps}{(CrO_4)}^{-2}}{{(CrO_4)}^{-2}}}=\sqrt{\frac{2.10^{-12}}{0,1}}=4,47.10^{-6} \, M
\\[0.5cm]
[ Ag^{+} ]=\frac{K_{ps} (AgCl)} {Cl^{-}}=\frac{1,7.10^{-10}} {0,05}= 3,4.10^{-9} ~M
\\[1cm]
\text{Per tant, precipitarà primer el clorur d’argent.}
\\[0.5cm]
\text{2. Quan comença a precipitar el cromat d’argent, la } [ Ag^{+} ] \text{ és } 4,47.10^{-6}
\\[0.5cm]
\text{En aquest punt de precipitació simultània:}
\\[0.5cm]
[ Cl^{-} ]=\frac{ K_{ps}(AgCl) } {[ Ag^{+} ]}=\frac{ 1,7.10^{-10}} { 4,47.10^{-6}}=3,8.10^{-5} \,M
}
\)

Calculeu si es formarà precipitat de $BaSO_4$ quan es barregen $80 \, cm^3$ d’una dissolució 0,01 M de sulfat de sodi amb $120 \, cm^3$ d’una altra dissolució 0,01M de nitrat de bari.

\(
\displaystyle{
\text {La reacció de precipitació del }Ba(SO_4) \text { és:}
\\[0.5cm]
\begin {matrix}
BaSO_4 &⇌& Ba^{+2} &+& SO_4^{-2}, \, K_s ( BaSO_4 )=1,1.10^{-10}
\end {matrix}
\\[0.5cm]
\text {I les de dissociació de les sals són:}
\\[0.5cm]
\begin {matrix}
Na_2(SO_4) &\rightarrow & 2Na^{+} &+& (SO_4)^{-2} \\
0 &\rightarrow & 2.0,01 &+ & 0,01 \\
Ba(NO)_{3} &\rightarrow& Ba^{+2} &+& 2 NO_3^{-} \\
0 &\rightarrow& 0,01 &+ & 2.0,01
\end {matrix}
\\[1.5cm]
\text{La concentració de } SO_4^{-2} \text{ després de fer la barreja és:}
\\[1cm]
[ SO_4^{-2} ]=\frac{0,01M \cdot 80.10^{-3} \text{ mols}} { 80.10^{-3}+120.10^{-3} \text{ L}}=0,004M
\\[1cm]
\text{La concentració de } Ba^{+2} \text{ després de fer la barreja és:}
\\[0.5cm]
[ Ba^{+2} ]=\frac{0,01M \cdot 120.10^{-3} \text{ mols}} { 80.10^{-3}+120.10^{-3} \text{ L}}=0,06M
\\[1cm]
\text {Per tant, el producte iónic del sulfat de bari format, serà:}
\\[1cm]
Q( BaSO_4 )=[ Ba^{+2} ][ SO_4^{-2} ]=0,06M \cdot 0,004=2,4.10^{-4}
\\[1cm]
\text {Com que } Q>(K_{ps}), \text{ precipitarà } Ba(SO_4)
}
\)

Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?

Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.

Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons

Al vostre fill li cal reforç de primària?

Ajudem al vostre fill a comprendre els continguts bàsics
Reforç en matemàtiques i comprensió lectora
L’ajudem a fer els deures d’estiu
Classes individuals en grups reduïts
Tardes de 17 a 19 h

Una base sòlida de primària és important per a fer l’ESO

Aprofiteu aquest estiu i apunteu-lo a reforç!

Classes de reforç i repàs d’estiu

Centre d’Estudis Edukat

Reforç escolar i Tècniques d’estudi

Primària – ESO – Batxillerat – Proves d’accés – Fpro – Universitat

T’has quedat enrere aquest any?

Vols preparar-te el curs que ve?

√ Classes de reforç els mesos de juliol i agost

√ Matins i tardes de dilluns a divendres

√ Classes individuals en grups reduïts

√ T’ajudem a fer els deures d’estiu

√ Onze anys d’experiència ajudant estudiants

Som especialistes en reforç escolar!

Apunteu-vos-hi ara!

Formulari de contacte

Nom

Cognom

Telèfon *

Correu-e

Assumpte

Missatge

INFORMACIÓ PROTECCIÓ DE DADES DE XAVIER MAS I RAMON (CENTRE ESTUDIS EDUKAT)

Finalitats: Respondre a les seves sol·licituds i remetre-li informació comercial dels nostres productes i serveis, fins i tot per correu electrònic. Legitimació: Consentiment de l'interessat. Destinataris: No estan previstes cessions de dades. Drets: Pot retirar el seu consentiment a qualsevol moment, així com accedir, rectificar, suprimir les seves dades i altres drets a centre.estudis.edukat@ceedukat.es. Informació Addicional: Pot ampliar la informació a l'enllaç d'Avisos Legals.

Obligatori

Accepto rebre informació comercial, fins i tot per correu electrònic.

Obligatori

He llegit i accepto la Política de Privacitat.

If you are human, leave this field blank.

Teoria àcid base

Instruccions abans de començar

1. Introducció

El 1884 el químic suec Arrhenius afirma en la teoria de dissociació iònica que, en dissolució aquosa, algunes substàncies es dissocien en ions positius i ions negatius que les fa conductores de l’electricitat.

Segons Arrhenius, un àcid és una substància que en dissolució aquosa es dissocia formant ions hidrogen ($H^+$) i una base es dissocia formant ions hidroxil ($OH^-$).

$
AH + H_2 O ⇌ A^- + H^+
\\
BOH + H_2 O ⇌ B^+ + OH^-
$

Però hi ha substàncies que es comporten com a àcids o com a bases en dissolvents que no són aigua o que no es dissocien en aquests ions.

El 1923, Brönsted i Lowry ampliaren de forma independent la definició d’àcid i base d’Arrhenius dient que, un àcid és una espècie química que pot proporcionar ions $H_ 3 O^+$ i una base en pot acceptar.

Quan un àcid perd un protó es forma la base conjugada, i quan una base en rep un és forma l’àcid conjugat de la base:

$
HA \text{(Àcid)} ⇌ A^- \text{(Base conjuagada)} + H^+
\\
BOH \text {(Base)} ⇌ B^+ \text { (Àcid conjugat)} + OH^-
$

Més tard, Lewis amplia encara més la definició i diu que un àcid és una substància que pot acceptar un parell d’electrons i una substància bàsica proporciona un parell d’electrons.

Tanmateix, les substàncies sols mostraran el caràcter àcid o bàsic quan reaccionin amb altres substàncies que puguin rebre o donar protons. Hi ha substàncies, com l’aigua, que de vegades tenen caràcter àcid o bàsic segons la substància amb la qual reaccioni.

2. Equilibri iònic de l’aigua

La reacció d’ionització de l’aigua és una reacció en la qual una molècula d’aigua perd un protó i esdevé un ió hidroxil $(OH^-)$. El nucli d’hidrogen ($H^+$) agafa immediatament una molècula d’aigua per a formar un ió oxoni ($H_3 O^+$):

$2H_2 O ⇌ H_3 O⁺ + OH^-$

tot i que Arrhenius va proposar inicialment la reacció d’ionització

$H_2 O ⇌ H⁺ + OH^-$

A causa de l’autoionització, l’aigua té una conductivitat elèctrica de 0.055 μS/cm.

La constant d’equilibri d’aquesta reacció és:

$\displaystyle K_e=\frac{[ H_3 O^+] \cdot [OH^-]} {[H_2 O]^2}$

A 25 ºC les concentracions d’ions hidroni i hidroxil són iguals:

$[H_3 O^+]=[OH^-]=1×10^{-7}$

I si calculem $H_2 O$ a partir de la densitat de l’aigua a 25ºC:

$\displaystyle [H_2 O]=0,997 \frac{g}{mL} \cdot {\frac{ 1 mol} {18g}} \cdot { \frac{1000 mL}{1L} }~=55,3 M$

Com que hi ha molt poques molècules dissociades, aproximadament 2 ppb, la reacció d’autoionització està desplaçada molt cap a l’esquerra i, per tant, la concentració d’aigua pràcticament no varia:

$\displaystyle K_e \cdot [H_2 O]^2={[ H_3 O^+] \cdot [OH^-]} \rightarrow K_w={[ H_3 O^+] \cdot [OH^-]}=10^{-14}$

3. Grau d’acidesa (pH o potencial d’hidrogen)

L’acidesa és la capacitat d’una substància de proporcionar protons en solució aquosa.

L’escala de pH es defineix usant un elèctrode d’hidrogen o de vidre en contacte amb la solució estudiada i un altre elèctrode de referència (de calomelans, per exemple). Un elèctrode de referència té un potencial de reducció estable i conegut. L’estabilitat del potencial de l’elèctrode s’aconsegueix mitjançant un sistema redox amb concentracions tampó.

El pH és una escala que varia logarítmicament de 0 (molt àcid) a 14 (molt poc àcid) en dissolucions aquoses:

$pH=-log [H_3 O^+]$

El pH de l’aigua pura és 7, però varia quan hi afegim un àcid o una base. Per la constant de l’aigua, quan augmenta la concentració d’ions oxoni, minva la d’hidroxils. La constant de l’aigua també varia amb la temperatura:

$K_w=[H_3 O^+] \cdot [OH^-]=10^{-14}, pK_w=pH+pOH=14$

El pH fou definit el 1909 pel químic danès Søren Peter Lauritz Sørensen.

4. Àcids i bases febles

Un àcid feble és un àcid que té poca capacitat de cedir protons. Una base feble és una base que té poca capacitat d’acceptar-los (l’àcid acètic o l’àcid carbònic són àcids febles i l’hidròxid d’amoni és una base feble, per exemple).

Un àcid/ base forta és un àcid/base que té molta capacitat de cedir/acceptar protons (l’àcid sulfúric o clorhídric són àcids forts i l’hidròxid de sodi o de potassi són bases fortes, per exemple).

Si l’àcid ($HA$) és feble, la base conjugada ($A^-$) serà forta (tindrà molta capacitat per a acceptar protons).

$HA ⇌ A^- + H^+$

En canvi, si l’àcid és fort, la base conjugada serà feble (tindrà poca capacitat per a acceptar protons).

$HA \rightarrow A^- + H^+$

De la mateixa manera, si una base és feble, l’àcid conjugat serà fort i a l’inrevés.

Els àcids o bases febles tenen constants de dissociació més petites que la unitat. Són reaccions de dissociació reversibles. En canvi, els àcids o bases fortes tenen constants de dissociació grans i són pràcticament irreversibles.

La constant d’equilibri d’un àcid feble és:

$\displaystyle K_a=\frac{[A^-] \cdot [H^+]} {[HA]}$

Similarment, la d’una base feble és:

$\displaystyle K_b=\frac{[B^+] \cdot [OH^-]} {[BOH]}$

Els claudàtors indiquen la concentració molar en l’equilibri de cada espècie.

A l’equilibri, la concentració d’ions hidrogen en un àcid és:

$
\displaystyle
[ H^+ ]=[ A^- ], [H A]=C_{inicial àcid }-[ H^+ ] \rightarrow [ H^+ ]=\sqrt{ K_a(C_{inicial àcid }-[ H^+ ])}
$

Si la concentració d’ions hidrogen és petita comparada amb la concentració inicial de l’àcid sense dissociar-se:

$
[ H^+ ]=\sqrt{ K_a C_{inicial àcid}}
\\
[ HA ]~=C_{inicial àcid}
$

(Vegeu l’entrada Equilibri Químic per a saber-ne més)

5. Efecte de l’ió comú

Com en qualsevol procés en equilibri, la ionització d’un àcid o d’una base feble pot estar influenciada per variacions de la concentració d’algun dels ions dissociats segons el principi de Le Chatêlier.

$HAc ⇌ Ac^- + H^+$

Per exemple, l’equilibri de la dissociació de l’àcid acètic es desplaçarà cap a l’esquerra si hi afegim ions acetat o un àcid, i es desplaçarà cap a la dreta si hi afegim una base.

Exemple:

$
\displaystyle{
\text{Quant minva la } H^+ \text{ d’una dissolució 0,20M d’àcid acètic quan s’hi afegeix NaAc 0,10M?}
\\
~K_a=1,8×10^{-5}
\\[0.5cm]
H^+= K_a \cdot { \frac{[HAc]} {~[Ac^-]} }=1,8×10^{-5}
\\[0.5cm]
\text{Abans d’afegir-hi NaAc, }[H^+]=[Ac^-]\text {:}
\\[0.5cm]
[H^+]^2= K_a \cdot {[HAc]}=1,8×10^{-5} \cdot 0,20=\sqrt {3,6×10^{-6}M}=1,90×10^{-3}M
\\[0.5cm]
\text{Després d’afegir-hi NaAc:}
\\[0.5cm]
H^+= K_a \cdot { \frac{[HAC]} {~[Ac^-]} }=1,8×10^{-5} \cdot { \frac{0,20} {0,10} }=3,6×10^{-6}M
\\[0.5cm]
\text{De fet, la concentració d’} AcH\text{ en l’equilibri és } 0.20+[H^+] \text{ i la d’ } [Ac^-]=0.10-[H^+],
\\
\text{ però podem fer l’aproximació anterior sense gaire error.}
}
$

Exemple:

\(
\displaystyle{
\text{Calculeu la concentració d’} H^+ \text{d’una dissolució formada per volums iguals d’HCl 0,10M}
\\
\text{i NaAc 0,40M.}
\\[0.5cm]
HCl \rightarrow H^+ (0,1M ) + Cl^-
\\
NaAc \rightarrow Na^+ + Ac^- ( 0,40M )
\\[0.5cm]
\text{Quan es barregen l’àcid clorhídric i l’acetat sòdic, 0,10mols de l’acid reaccionen amb}
\\
\text{ 0,10 mols de la sal i s’estableix l’equilibri:}
\\[0.5cm]
\begin{matrix}
Ac^- & + & H^+ & ⇌ & HAc \\
(0,40-0,10):2 & + & H^+ & ⇌ & 0,10:2\end{matrix}
\\
[ H^+]=K_a \cdot { \frac{[HAc]} {[Ac^-] }}=1,8×10^{-5} \cdot {\frac{0,050} {0,15}}=6,0×10^{-6}M
\\[0.5cm]
\text{Les concentracions en l’equilibri d’acetat i HAc s’han de dividir per dos perquè s’afegeixen}
\\
\text{volums iguals de cada reactiu.}
\\[0.5cm]
\text{De fet, }[ HAc ]=0,050-[H^+] \, i \, [ Ac^- ]=0,15+[H^+] \text{, però la concentració d’ions hidrogen és}
\\
\text{tan petita comparada amb la d’àcid i d’acetat que l’error que fem menyspreant-la}
\\
\text{és molt petit.}
}
\)

(Vegeu l’apartat 7. Hidròlisi d’aquest document)

6. Dissolucions amortidores, reguladores o tampó

Les dissolucions amortidores, reguladores o tampó són dissolucions el pH de les quals varia molt poc per dilució o addició de quantitats moderades d’àcids o de bases, fins i tot forts. Una solució està amortida, tamponada o regulada si s’oposa a la modificació de la concentració d’ions oxoni.

Estan formades per un àcid o una base feble i una de les seves sals fortament ionitzada.

Un compost que tingui a la vegada propietats àcides o bàsiques pot ser regulador de pH.

Per exemple, una dissolució de bicarbonat ($HCO_3 ^-$) té acció reguladora a causa d’aquest ió que pot cedir o acceptar protons quan reacciona amb altres àcids o bases:

$
H CO_3^- + OH^- ⇌ H_2 O + CO_3^{–}
\\
H CO_3^- + H^+ ⇌ H_2 CO_3
$

En general, les sals d’àcids polipròtics febles tenen acció reguladora petita.

Exemple:

\(
\displaystyle{
\text{La constant d’ionització d’un àcid feble és } K_a=1,0.10^{-5}.
\\
\text{Es preparen dues solucions 0,10M, una d’aquest àcid i l’altra de la seva sal sòdica.}
\\
\text{Calculeu el pH de la solució original i de la solució després d’afegir-hi 0,010 mols d’HCl }
\\
\text{i després d’afegir-hi 0,010 mols d’NaOH a un litre de solució reguladora.}
\\[0.5cm]
HA ⇌ H^+ + A^- \rightarrow [H^+]=K_a \cdot { \frac{[HA]}{ [A^-] }} \rightarrow pH=pK_a+log{\frac{[A^-]} {[HA]}}
\\[0.5cm]
\text{a) Abans d’afergir-hi l’àcid o la base:}
\\[0.5cm]
pH=pK_a+log{\frac{[A^-]} {[HA]}}=5+log{\frac{ 0,1 }{ 0,1 }}=5
\\[0.5cm]
\text{b) Després d’afegir-hi l’àcid l’equilibri es desplaçarà cap a l’esquerra:}
\\[0.5cm]
[ HA ]= 0,11, \, [ A^- ]=0,09 \rightarrow pH=pK_a+log{\frac{[A^-]}{[HA]}}=5+log{\frac{ 0,09 }{ 0,11 }}=4,91
\\[0.5cm]
\text{c) Després d’afegir-hi la base l’equilibri es desplaçarà cap a la dreta:}
\\[0.5cm]
[ HA ]= 0,09, \, [ A^- ]=0,11 \rightarrow pH=pK_a+log{\frac{[A^-]}{[HA]}}=5+log{\frac{ 0,11 } { 0,09 }}=5,09
}
\)

7. Hidròlisi

La hidròlisi és la descomposició d’una substància per l’acció de l’aigua sense transferència d’electrons. La sal d’un àcid feble i d’una base forta, la d’una base feble i d’un àcid fort i la d’un àcid i una base febles tenen tendència a hidrolitzar-se. Si és una reacció irreversible, la hidròlisi és completa:

$PCl_3 + 3H_2 O \rightarrow 3HCl + H_3 PO_3$

Però si la reacció és reversible, com en el cas d’algunes sals, s’estableix un equilibri:

7.1 D’una reacció d’anions d’àcids febles

$
\displaystyle{
A^- + H_2 O ⇌ HA + OH^-
\\
K_{conjuagada}= \frac{[HA][OH^-]} {[A^-]}
}
$

En una reacció d’hidròlisi intervenen dues reaccions d’equilibri, la $A^-$ de la sal i la $OH^-$ de l’aigua, les quals competeixen pels $H^+$ :

$
\displaystyle{
HA ⇌ A^- + H^+
\\
H_2 O ⇌ OH^-+ H^+
\\[0.5cm]
K_a=\frac{[ H^+ ][A^-]} {[HA]} \rightarrow [ H^+ ]= K_a \cdot \frac{[HA]} {[A^-]} \, i,
\\
K_{H_2 O}=[ H^+ ][ OH^-] \rightarrow [ H^+ ]= \frac{K_{H_2 O}} {[ OH^-]}
\\
K_a \cdot \frac{[HA]} {[A^-]}=\frac{K_{H_2 O}} {[ OH^-]} \rightarrow [HA][ OH^-]=\frac{K_{H_2 O}} {K_a} [A^-]
\\
\text{Quan s’arriba a l ‘equilibri:} [HA]=[ OH^-] \rightarrow [ OH^-]=\sqrt{\frac{K_{H_2 O}} {K_a} [A^-]}
\\
pH=14-pOH
\\[0.5cm]
\text{O bé:}
\\[0.5cm]
K_{hidròlisi}=\frac{[HA][OH^-]} {[A^-][H_2 O]} \rightarrow K_{conjugda}=\frac{[HA][OH^-]} {[A^-]}
\\
[ OH^-]=\sqrt{K_{conjugada} \cdot [ A^- ]}=\sqrt{\frac {K_{H_2 O}} {K_a} \cdot [ A^- ]}
\\
pH=14-pOH
}
$

7.2 D’una reacció de cations de bases febles

$B^++H_2 O ⇌ BOH+ + H^+$

En aquest cas, $B^+$ i els $H^+$ de l’aigua competeixen pels $OH^-$:

$
\displaystyle{
BOH ⇌ OH^- +B^+
\\
H_2 O ⇌ OH^-+ H^+
\\[0.5cm]
[ H^+]=\sqrt{ K_{conjugada} \cdot [ B^+ ]}=\sqrt{\frac {K_{H_2 O}} {K_b} \cdot [ B^+ ]}
\\
pH=-log(\sqrt{\frac {K_{H_2 O}} {K_b} \cdot [ B^+ ]})
}
$

8. Neutralització (Valoracions àcid-base)

La reacció entre un àcid i una base produeix una sal i aigua:

$HA +B(OH) ⇌ BA+ H_2 O$

Hi ha diferents valoracions de neutralització depenent de la força de l’àcid i de la base.

Una valoració és possible si, l’error relatiu del canvi que indica el final de la reacció al volum de valorat, és de l’1 o el dos per mil (una o dues gotes -una gota=0,05 ml- de valorant en 50 ml de valorat).

És important saber el pH aproximat de neutralització d’una reacció per tal d’escollir bé l’indicador adequat.

En una reacció de neutralització:

$V_{valorant} \cdot N_{valorant}=N_{valorat} \cdot V_{valorat}$

En funció de la molaritat:

$V_{valorant} \cdot (M_{valorant} \cdot \nu)=V_{valorat} \cdot (M_{valorat} \cdot \nu)$

$\nu$ és el nombre d’equivalents gram de la substància.

(Vegeu MESCLES I BARREGES, 1.3 Concentració per a saber-ne més.)

8.1 D’un àcid fort i una base forta

La reacció en aquest cas és $H^+ + OH^- ⇌ H_2 O$. A la vora del punt estequiomètric, el canvi de pH és molt ràpid. La mesura del pH es fa amb un pH- metre o un potenciòmetre. El pH del punt final es pot detectar amb el canvi de color d’un indicador.

En una valoració sempre es compleix que:

$
N_{valorant} \cdot V_{valorant}=N_{valorat} \cdot V_{valorat}
\\
M_{valorant} \cdot \nu_{valorant} \cdot V_{valorant}=
M_{valorat} \cdot \nu_{valorat} \cdot V_{valorat}
$

Exemple:

\(
\displaystyle{
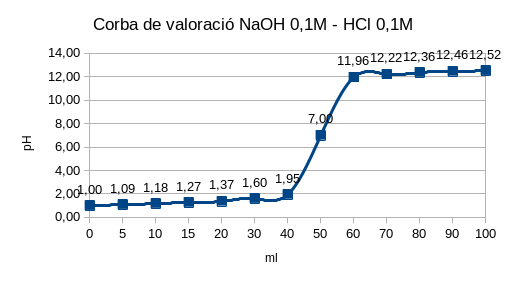
\text{Valoració de 50,00 ml de HCl 0,1 N amb NaOH 0,1 N -en aquest cas } \nu_{valorant}=\nu_{valorat}=1:
\\[0.5cm]
\text{A efectes de calcular el pH, la reacció és } H^+ + OH^-⇌ H_2 O
\\
\text{És a dir, que la concentració de NaOH és igual a la concentració d’} OH^-
\\
\text{i la concentració d’HCl és igual a la concentració d’H^+}
\\[0.5cm]
\text {a. Abans d’afegir la base:}
\\[0.5cm]
\text {Abans d’afegir la base el pH és el de la dissolució de clorhídric.}
\\
\text{Com que el clorhídric és un àcid fort, considerem que està}
\\
\text{completament dissociat. En aquest cas la normalitat és igual}
\\
\text{a la molaritat, i el pH=-log ( 0,1 )=1,00.}
\\[0.5cm]
\text {b. Quan s’han afegit 10,00 ml de NaOH:}
\\[0.5cm]
\text{Com que 1 meg (1 mol) de NaOH (OH^-) neutralitzarà 1 mol d´HCl} (H^+)
\\
\text{i el volum total de solució serà de 60,0 00 ml:}
\\[0.5cm]
[ H^+ ]=\frac{\text {mols HCl restants en dissolució}}{\text{Volum total dissolució}}
\\
\frac{\text{ mols HCl inicials – mols HCl neutralitzats}} {\text{Volum total dissolució}}=\frac{ 5-1 } {60 }=\frac{1}{15}M
\\
pH=-log[ H^+]=1.17
\\[0.5cm]
\begin {Bmatrix}
\text{mols HCl inicials}=0,1N \cdot 50,00ml=5 \\
\text{mols NaOH neutralitzats}=0,1N \cdot \text{V afegit NaOH}\\
\text{Volum total dissolució}=50,00ml+\text{V afegit NaOH}
\end {Bmatrix}
\\[1cm]
\text{3. En afegir-hi 25,00 ml de base:}
\\[0.5cm]
[ HCl ]= [H^+ ]\frac {\text{mols HCl restants en dissolució}} {\text{Volum total dissolució}}=
\\
\frac{\text{mols HCl inicials} – \text{mols HCl neutralitzats}} {\text{Volum total dissolució}}=\frac{ 5-2,5 } {75,00 }=\frac{1}{30}M
\\
pH=-log(1/30)=1.48
\\[0.5cm]
\begin {Bmatrix}
\text{mols HCl inicials}=0,1N \cdot 50,00ml=5
\\
\text{mols HCl neutralitzats}=0,1N \cdot \text{V afegit NaOH}=2,5 \text{ mols}
\\
\text{Volum total dissolució=50,00ml+V afegit NaOH}
\end {Bmatrix}
\\[1cm]
\text{4. En el punt estequiomètric:}
\\[0.5cm]
M_{HCl} \cdot V_{HCl}=M_{NaOH} \cdot V_{NaOH} \rightarrow V_{NaOH}=\frac{0.1M \cdot 50,00 ml}{0.1}=50,00 ml NaOH
\\
pH=7 ([H_3O^+]=[OH^-])
\\[1cm]
\text{5. Després del punt estequiomètric: es calcula el pH per l’excés de NaOH afegit.}
\\
\\ \text{Havent afegit 60,00 ml de NaOH:}
\\
pH=14-pOH=14+log(\frac{0.1 \cdot 10.00 \enspace ml}{110\enspace ml})=12
\\
\\
\text{Els càlculs de la valoració d’una base feble amb un àcid fort són similars als anteriors.}
}
\)

Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?

Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.

Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons

Cinètica química

Instruccions abans de començar

1. Introducció

La cinètica química és la branca de la química que estudia la velocitat i els mecanismes de reacció de les reaccions químiques en diferents condicions, mentre que la termodinàmica estudia en quin sentit es produirà la reacció.

L’estudi de la influència de diferents condicions ens dóna informació dels mecanismes i dels estats de tansició de les reaccions.

La velocitat d’una reacció és la variació de la concentració dels reactius i els productes en el temps. El 1864, Guldberg i Waage van descobrir que la velocitat d’una reacció química és proporcional a la concentració dels reactius. Foren els pioners de la cinètica química.

2. L’energia d’activació i el complex activat

$aA+bB ⇌ cC+dD$

El complex activat és la configuració atòmica dels reactius en el punt de màxima energia de la reacció. Aquesta configuració és el punt de transició de la reacció, quan els reactius es transformen en els productes. Després d’aquest punt, l’energia de la reacció comença a minvar fins a estabilitzar-se en la dels productes.

La diferència entre l’energia del complex activat i la dels reactius és l’energia d’activació de la reacció directa. La diferència entre l’energia del complex activat i la dels productes és l’energia d’activació de la reacció inversa. És l’energia mínima que cal perquè es produeixi la reacció.

El gràfic anterior mostra com varia l’energia d’una reacció exotèrmica (l’energia dels productes és més petita que la dels reactius).

3. Mecanismes de reacció

El mecanisme d’una reacció són les reaccions en seqüència que transformen els reactius en productes. També descriu la termodinàmica i totes les característiques qualitatives i quantitatives de la reacció. És una descripció teòrica suportada per evidències experimentals que la confirmen.

Els reactius intermedis d’un mecanisme de reacció són espècies químiques inestables i vida curta que no són part de la reacció química global. Generalment, són radicals lliures o ions.

Cada etapa del mecanisme de reacció té una velocitat i molecularitat pròpies (nombre de molècules que reaccionen en una etapa). L’etapa més lenta del mecanisme de reacció determina la velocitat de la reacció global.

$
\mathbf {CH_4 +4Cl_2 ⇌ CCl_4 + 4HCl}
\\[0.5cm]
\mathbf{CH_4+Cl_2} ⇌ CH_3 Cl+HCl
\\
CH_3 Cl+Cl_2 ⇌ CH_2 Cl_2+HCl
\\
CH_2 Cl_2 + Cl_2 ⇌ CHCl_3 + HCl
\\
CHCl_3 + Cl_2 ⇌\mathbf {CCl_4 + HCl}
$

La cinètica química i altres tècniques (com l’efecte de la temperatura i l’espectroscòpia, per exemple) ens serveix per a esbrinar la velocitat, l’ordre i el mecanisme d’una reacció.

4. Velocitat, constant i ordre de reacció

4.1 Velocitat de reacció

La velocitat mitjana d’una reacció és:

$
\displaystyle{
\bar v= -\frac { [A]_0 }{a \Delta t }=-\frac{ [B]_0 } {b \Delta t }=\frac{ [C] }{c \Delta t }=\frac{ [D] } {d \Delta t }
}
$

I la velocitat en un moment determinat del temps és:

$
\displaystyle{
v_i=-\frac{1} {~a} \frac{[A]_0 } { dt }=-\frac{1} {~b} \frac {[B]_0 } { dt }=-\frac{1} {~c} \frac {[C] } { dt }=-\frac{1} {~d} \frac{[D] } { dt }
}
$

L’equació de velocitat determina la velocitat instantània d’una reacció amb les concentracions inicials dels reactius en un moment del temps.

$
\displaystyle{
v_i=k \cdot [ A ]^\alpha_0 \cdot [ B ]^\beta_0
}
$

L’energia lliure de Gibbs ens diu si una reacció es produirà o no, però no ens diu si serà ràpida o lenta. La velocitat d’una reacció la determina la cinètica química.

4.2 Constant de reacció (k)

La constant de velocitat és una constant de proporcionalitat que fa la igualtat de l’equació de velocitat. És específica de cada reacció i depèn de la temperatura (equació Arrhenius). S’ha de determinar experimentalment.

$
\displaystyle{
k=A \cdot e^{-\frac{ E_a } { RT }} \rightarrow \ln k=\ln A-\frac{ E_a } { RT }
}
$

4.3 Ordres de reacció

L’ordre parcial de reacció d’un reactiu és l’exponent de la concentració d’aquest reactiu en l’equació de velocitat. L’ordre global de la reacció és la suma dels exponents de les concentracions dels reactius de l’equació.

$
\displaystyle{
v_i=k \cdot [ A ]^\alpha_0 \cdot [ B ]^\beta_0
}
$

L’ordre global de l’equació anterior és $\alpha+\beta$

4.4 Variació de la velocitat de reacció

La velocitat de reacció depèn de la concentració, de la temperatura, dels catalitzadors i de la pressió, però també s’ha de tenir en compte la natura i l’estat físic dels reactius:

4.4.1 Concentració

Les col·lisions de les molècules dels reactius determinen la velocitat d’una reacció. Si la concentració és més alta, hi haurà més col·lisions i, per tant, la velocitat augmentarà.

4.4.2 Temperatura

La temperatura afecta molt la velocitat de reacció. Com més alta sigui, més gran serà l’energia tèrmica de les molècules. Això farà augmentar en nombre de col·lisions i conseqüentment, la velocitat de la reacció.

Segons Arrhenius, la constant de la velocitat de reacció, és funció de la temperatura i de l’energia d’activació:

$
\displaystyle{
k=A \cdot e^{-\frac{ E_a } { RT }}
}
$

4.4.3 Catalitzadors

La presència de catalitzadors canvien el mecanisme de reacció i fan minvar l’energia d’activació, tot i que es manté la termodinàmica de la reacció. Els catalitzadors resten inalterats al final de la reacció, malgrat que perden activitat amb el temps.

4.4.4 Pressió

En augmentar la pressió augmenta la quantitat de col·lisions entre els reactius i això fa augmentar la velocitat de reacció.

4.4.5 Natura i estat físic dels reactius

La velocitat de reacció també depèn de la natura i de l’estat físic dels reactius: les reaccions iòniques són més ràpides que les de formació d’enllaços covalents i l’estat físic fa que l’eficàcia de les col·lisions depengui de l’àrea de contacte dels reactius.

Exemples

Determinació de l’equació de velocitat

\(
\displaystyle{
\begin {matrix}
Essaig & {}:{} & [CH_3 Cl]_0 & {}:{} & [H_2 O]_0 & {}:{} & \text{ velocitat reacció}
\\
1 & {}:{} & 0,25 & {}:{} & 0,25 & {}:{} & 2,83
\\
2 & {}:{} & 0,25 & {}:{} & 0,50 & {}:{} & 11,35
\\
3 & {}:{} & 0,50 & {}:{} & 0,25 & {}:{} & 5,675
\end {matrix}
\\[2cm]
\text{ L’equació de la velocitat de reacció es:}
\\[0.5cm]
v=k \cdot [ CH_3 Cl ]^\alpha _0 \cdot [ H_2 O ]^\beta _0
\\[0.5cm]
\text{ Per a definir l’equació de la reacció anterior hem de trobar la constant i }
\\
\text{els ordres parcials de la reacció:}
\\[0.5cm]
\text{ Calcularem l’ordre } \beta \text{ eliminant l’ordre } \alpha:
\\[0.5cm]
v_1=k \cdot 0,25^\alpha \cdot 0,25^\beta
\\
v_2=k \cdot 0,25^\alpha \cdot 0,50^\beta
\\
\frac{ v_1 } { v_2 }=\frac{ k \cdot 0,25^\alpha \cdot 0,25^\beta } { k \cdot 0,25^\alpha \cdot 0,50^\beta }=\frac{ 0,25^\beta } { 0,50^\beta }\rightarrow \frac{ 2,83 } { 11,35 }=( \frac{0,25} {0,50} )^\beta\rightarrow ln 0,25=\beta \cdot ln 0,50\rightarrow \beta=2
\\[1cm]
\text{ Calcularem l’ordre } \alpha \text{ eliminant l’ordre } \beta:.
\\[0.5cm]
v_1=k \cdot 0,25^\alpha \cdot 0,25^\beta
\\
v_3=k \cdot 0,50
\frac{ v_1 } { v_3 }=\frac{ k \cdot 0,25^\alpha \cdot 0,25^\beta } { k \cdot 0,50^\alpha \cdot 0,25^\beta }=\frac{ 0,25^\alpha } { 0,50^\alpha }\rightarrow \frac{ 2,83 } { 5,675 }=( \frac{0,25} {0,50} )^\alpha
\\
ln 0,50=\beta ln 0,50 \rightarrow \alpha=1
\\[1cm]
\text{ Per acabar, determinem la k:}
\\[1cm]
v_1=k \cdot 0,25^\alpha \cdot 0,25^\beta\rightarrow2,83=k \cdot ( 0,25 )^1 \cdot ( 0,25 )^2
\\[0.5cm]
k=\frac{ 2,83 } { (0.25)^1 \cdot (0,25)^2 }={181.12 ~mols^{-3}.L^{4}.s^{-1} }
\\[1cm]
\text{Per tant,}
\\[1cm]
\mathbf{v=181.12[A]_0[B]_0^2}
}
\)

Determinació de la variació de l’energia d’activació d’una reacció

En una reacció química, la constant de velocitat es triplica si la temperatura
augmenta de 270 K fins a 308 K. Calcula l’energia d’activació de la reacció.

$
\displaystyle{
k=A \cdot e^{ -\frac{E_a} {RT} }
\\
\\
k_{270}=A \cdot e^{ -\frac{E_a} {R\cdot 270} }, k_{308}=A \cdot e^{ -\frac{E_a} {R\cdot 308} }
\\
\frac{k_{308}} {k_{270}}=\frac{A \cdot e^{ -\frac{E_a} {R.\cdot 308} }} {A \cdot e^{ -\frac{E_a} {R.\cdot 270}}
}\rightarrow
3=e^{ -\frac{E_a} {R\cdot 308}+\frac{E_a} {R.\cdot 270}}
\\
ln 3=-\frac{E_a} {8,314 \cdot 308}+\frac{E_a} {8,314 \cdot 270}
\\
ln 3 \cdot (8,314 \cdot 270 \cdot 8,314 \cdot 308)=-8,314 \cdot 270 E_a+8,314 \cdot 308 E_a
\\
E_a=\frac{ln 3 \cdot (8,314 \cdot 270 \cdot 8,314 \cdot 308)} {-8,314 \cdot 270+8,314 \cdot 308}=\mathbf {19 988.737J}
}
$

EXERCICIS PAU

Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?

Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.

Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons