Instruccions abans de començar
Definició
Un determinant és la suma dels productes de cada element d’una fila (o columna) pels de les altres files (o columnes). Cada producte sols pot tenir un element de cada fila (o columna).
Per a entendre millor aquesta definició, vegeu com es fa el càlcul de determinants per Sarrus d’una matriu \[A_{3*3}\].
Un determinat és un valor associat a una matriu quadrada. Un determinant és únic per a cada matriu.
Els determinants van ser introduïts inicialment a l’àlgebra per a resoldre la determinació del nombre de solucions d’un sistema d’equacions lineals.
Interpretació geomètrica
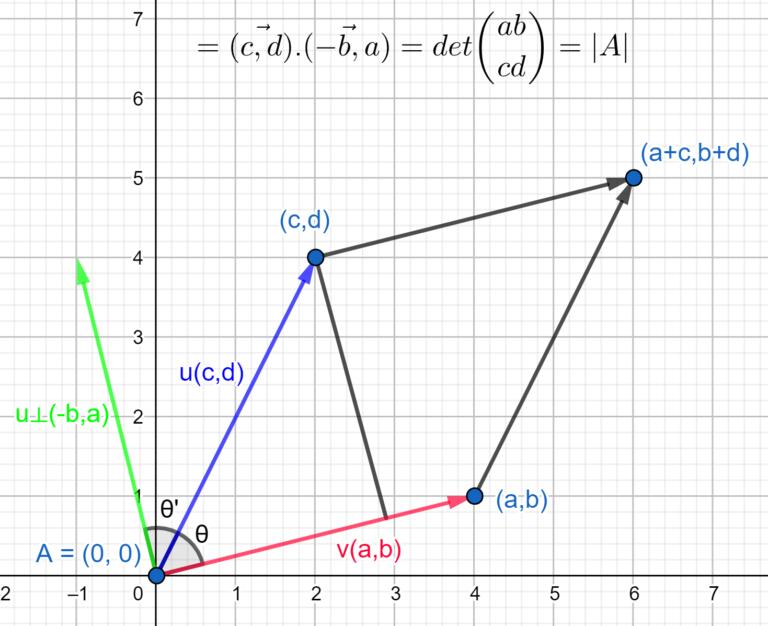
Les imatges dels vectors formen un paral·lelogram. El paral·lelogram definit per les files de la matriu anterior és el que té vèrtexs en \[(0, 0), (a, b), (a + c, b + d), (c, d)\]. El valor absolut \[ad-bc\] és l’àrea del paral·lelogram.
El valor absolut del determinant juntament amb el signe és l’àrea orientada al paral·lelogram. L’àrea orientada és la mateixa que l’àrea habitual, excepte que és negativa quan l’angle del primer al segon vector que defineix el paral·lelogram gira en sentit horari (regla de la mà dreta).
Els dos vectors d’una matriu \[u ≡ (a, b),v ≡ (c, d)\] representen els costats del paral·lelogram. L’àrea amb signe es pot expressar com \[\vec{| u |}.\vec{| v |}.sin θ\], que és l’alçària per la base del paral·lelogram o l’àrea del paral·lelogram.
Si representem aquesta expressió en funció de l’angle complementari de \[theta\]: \[\vec{| u ⊥ |}.\vec{| v |}.cos θ ′\], que és el producte escalar dels vectors \[\vec{ u ⊥}, \vec{ v}\]. És a dir,\[ (− b, a).(c,d)=ad-bc.\]
Propietats dels determinants
Les propietats dels determinants ens faciliten el seu càlcul. Aquestes propietats s’apliquen tant a les columnes com a les files de la matriu:
- Si bescanviem dues files o columnes d’una matriu, el valor del determinant canvia de signe.
\[\begin{vmatrix}1 & 6\\9 & 5\end{vmatrix}=5-54=-49\]
\[\begin{vmatrix}9 & 5\\1 & 6\end{vmatrix}=54-5=+49\]
- Quan multipliquem o dividim una fila o columna per un nombre, el resultat del determinant queda multiplicat o es dividit per aquest nombre.
\[\begin{vmatrix}\color{red}3*1 & 6\\ \color{red}3*9 & 5\end{vmatrix}
=
\begin{vmatrix}\color{red}3 & 6\\ \color{red}{27} & 5\end{vmatrix}
=
5*3-27*6=-147\]
- Quan a una fila (o columna) se li suma una combinació lineal d’una altra fila (o columna), el valor del determinant ni canvia.
\[
\begin{vmatrix}1 & 6\\9 & 5\end{vmatrix}
\\
C_2=C_2-2*C_1
\\
\begin{vmatrix}1 & \color {red}{6-2}\\ 9 & \color{red}{5-18}\end{vmatrix}
=
\begin{vmatrix}1 & \color {red}4\\ 9 & \color {red}{-13}\end{vmatrix}
=
-13-36=-49\]
- Quan una fila (o columna) és nu·la, el valor del determinant serà zero.
\[\begin{vmatrix}0 & 6\\ 0 & 5\end{vmatrix}
=
0*5-6*0=0\]
- Quan una fila (o columna) és combinació lineal d’altres files (o columnes), el determinant val zero.
\[\begin{vmatrix}1 & 6\\8 & 48\end{vmatrix}
=
48*1-6*8=0\]
Cálcul de determinants
Gauss-Jordan
L’algorisme de Gauss-Jordan aplicat a una matriu és el resultat de multiplicar-la per un nombre finit de matrius elementals.
Un cop hem fet la triangulació de la matriu per aquest mètode, el determinant de la matriu és el producte dels elements de la diagonal de la matriu.
\[ \begin{bmatrix} 1 & {-3} & {-1}\\ 1 & -4 & -3\\ 0 & 1 & 1 \end{bmatrix} \\ F_2=F_1-F_2 \\ \begin{bmatrix} \color{blue}1 & -3 & -1\\ \color{red}0 & \color{red}1 & \color{red}2\\ 0 & 1 & 1 \end{bmatrix} \\ F_3=F_2-F_3 \\ \begin{bmatrix} \color{blue}1 & -3 & -1\\ 0 & 1 & 2\\ \color{red}0 & \color{red}0 & \color{red}1 \end{bmatrix} \\ F_2=2F_3-F_2 \\ \begin{bmatrix} 1 & -3 & -1\\ \color{red}0 &\color{red} -1 &\color{red} 0\\ 0 & 0 &\color{blue}1 \end{bmatrix} \\ F_1=F_3+F_1 \\ \begin{bmatrix} \color{red}1 & \color{red}{-3} &\color{red} 0\\ 0 &{-1} &0\\ 0 & 0 & \color{blue}1 \end{bmatrix} \\ F_1=3F_2-F_1 \\ \begin{bmatrix} \color{red}{-1} &\color{red} 0 &\color{red} 0\\ 0 &\color{blue}{-1} & 0\\ 0 & 0 & 1 \end{bmatrix}\]I per tant,
\[\begin{vmatrix} 1 & {-3} &{-1}\\ 1 & -4 & -3\\ 0 & 1 & 1 \end{vmatrix} = \begin{vmatrix} -1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & 1 \end{vmatrix} = 1\]Fórmula de Laplace
Segons el teorema de Laplace, el determinant d’una matriu és la suma dels determinants dels adjunts de qualsevol fila (o columna) de la matriu:
\[\begin{vmatrix} \color{red}1 & -3 & {-1}\\ \color{red}1 & -4 & -3\\ \color{red}0 & 1 & 1 \end{vmatrix} = \color{red}+1*\begin{vmatrix} -4 & {-3}\\ 1 & -1 \end{vmatrix} \color{red}-1*\begin{vmatrix} -3 & -1\\ 1 & 1 \end{vmatrix} \color{red}+0*\begin{vmatrix} -3 & -1\\ -4 & -3 \end{vmatrix} = \\ \color{red}+1*\color{red}{-1}-1*-2+\color{red}0*5=1 \]El signe de l’adjunt d’un element \[a_{ij}\] és \[(-1)^{i+j}\]:
\[ sign(a_{11})=(-1)^{1+1}=+\\ sign(a_{12})=(-1)^{1+2}=-\\ sign(a_{13})=(-1)^{1+}=+\\ …\\ sign(a_{ij})=(-1)^{i+j} \]Sarrus
Si
\[ A_{3*3} = \begin{bmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{bmatrix} \]el \[det(A)\] usant el mètode de Sarrus és:
\[ \begin{bmatrix} \color{red}1&\color{green}{-3}&\color{blue}{-1}\\ \color{blue}1&\color{red}{-4}&\color{green}{-3}\\ \color{green}0&\color{blue}0&\color{red}1\end{bmatrix} = +(1*-4*1+1*1*-1+-3*-3*0)=-5 \\ \begin{bmatrix}\color{green}1&\color{blue}{-3}&\color{red}{-1}\\ \color{blue}1&\color{red}{-4}&\color{green}{-3}\\ \color{red}0&\color{green}0&\color{blue}1\end{bmatrix} = -(0*-4*-1+1*1*-3+1*-3*-3)=-6\\ \]I llavors, \[|A|=\]-5-(-6)=1.

 RSS CEEdukat
RSS CEEdukat