Instruccions abans de començar
1. Què és un sistema d’equacions
Un sistema d’equacions són dues o més equacions que compleixen certes igualtats per a uns valors determinats (solucions) de les incògnites.
Dues equacions són equivalents quan tenen les mateixes solucions.
El nombre de solucions d’un sistema és igual al grau de l’equació, tot i que en el conjunt dels nombres reals (\[\mathbb R\]) pot ser inferior quan apareixen arrels d’índex parell negatives com en aquest cas:
\[x^2-4x+8=0
\\
\Delta=\sqrt {b^2-4*a*c}
\\
\sqrt {4^2-4*1*8}
\\
\sqrt {16-32}
\\
\sqrt{-16}
\]
En aquest article, sols veurem la resolució de sistemes de dues equacions.
2. Classificació dels sistemes d’equacions
2.1 Segons el grau de les equacions
2.1.1.1 Lineals
Un sistema d’equacions és lineal quan tots els termes de les equacions són de grau u.
2.1.1.2 No lineals
Quan alguna o totes les equacions del sistema són de grau dos o superior, o bé són equacions no lineals, diem que és un sistema d’equacions no lineal.
2.2 Segons les soluciones del sistema
2.2.1 Sistema Compatible Determinat (SCD)
Un sistema és compatible determinat si té un nombre finit de solucions.
Per a què un sistema d’equacions sigui determinat, calen tantes equacions diferents com incògnites tingui el sistema.
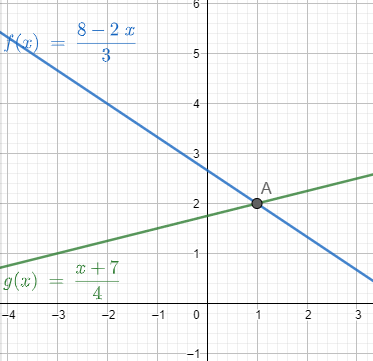
Dues rectes del pla que formen un sistema compatible determinat es tallen en un punt.
\[\begin {cases}
2x+3y=8
\\
x-4y=-7
\end {cases}
\\[1cm]
\begin {cases}
\hspace{0.2pt} +2x+3y=8
\\
-2x+8y=+14
\\
——————
\\
\hspace{9pt} 0x+11y=22
\end {cases}
\\[1cm]
\begin {cases}
y=\frac{22}{11}=2
\\[0.2cm]
x=\frac{8-3y}{2}=1
\end {cases}
\]
2.2.2 Sistema Compatible Indeterminat
Un sistema compatible indeterminat és un sistema d’equacions que té infinites solucions.
Si un sistema té més incógnites que equacions diferents, serà un sistema indeterminat.
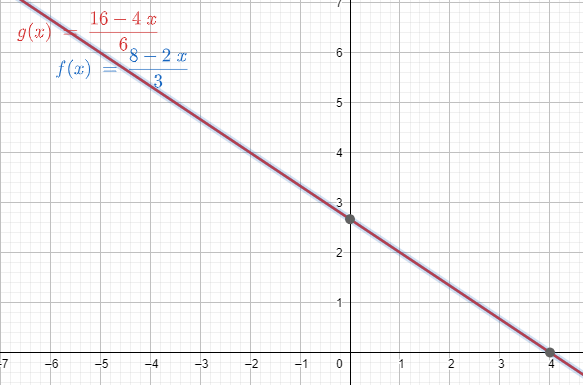
Si un sistema de dues funcions lineals del pla és indeterminat, les rectes que el formen són en realitat una mateixa recta.
\[\begin {cases}
2x+3y=8
\\
4x+6y=16
\\
\end {cases}
\\[1cm]
\begin {cases}
\hspace{0.2pt} +4x+6y=16
\\
-4x-6y=-16
\\
——————-
\\
\hspace{9pt} 0x+0y=0
\end {cases}
\]
2.2.3 Sistema Incompatible
Un sistema és incompatible si no té solució.
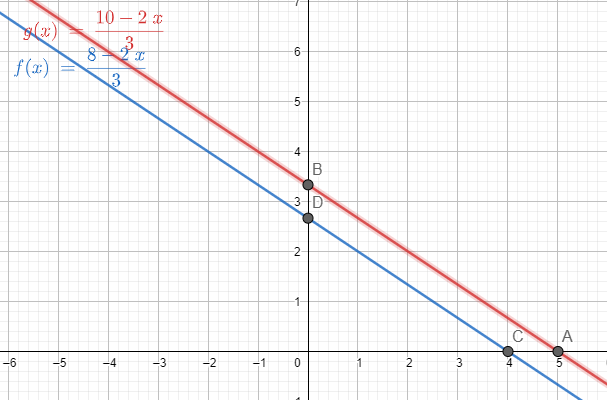
Quan dues rectes del pla són paral·leles, formen un sistema incompatible.
\[\begin {cases}
2x+3y=8
\\
2x+3y=10
\\
————-
\\
0=-2
\end{cases}
\]
(Per a saber-ne, vegeu Altres mètodes de resolució de sistemes d’equacions -Batxillerat).
3. Resolució del sistemes d’equacions
Al resoldre un sistema d’equacions determinem els punts secants (d’intersecció) de les equacions del sistema entre sí. Aquests són els punts que tenen en comú les equacions del sistema.
El nombre màxim de solucions serà el grau més gran de les equacions del sistema.
3.1 Lineals
3.1.1 Reducció o Eliminació
Consisteix en eliminar o reduir una de les incògnites del sistema d’equacions.
Per a eliminar-la, multiplicarem cada equació pel coeficient de la incògnita que volem eliminar de l’altre equació.
\[\begin {cases}
2x+3y=8
\\
x-4y=-7
\end {cases}
\\[1cm]
\begin {cases}
4*)\,2x+3y=8
\\
3*)\,x-4y=-7
\end {cases}
\\[1cm]
\begin {cases}
8x+12y=32
\\
3x-12y=-21
\end {cases}
\\[1cm]
\begin {cases}
\hspace{0.2pt} 11x+0y=11
\\
x=\frac{11}{11}=1
\\[0.2cm]
y=\frac{8-2x}{3}=2
\end {cases}
\\[1cm]
\begin {cases}
2x+3y=8
\\
x-4y=-7
\end {cases}
\\[1cm]
\begin {cases}
1*)\,2x+3y=8
\\
2*)\,x-4y=-7
\end {cases}
\\[1cm]
\begin {cases}
2x+3y=8
\\
2x-8y=-14
\end {cases}
\\[1cm]
\begin {cases}
\hspace{0.2pt} +2x+3y=8
\\
-2x+8y=+14
\end {cases}
\\[1cm]
\begin {cases}
\hspace{0.2pt} +2x+3y=8
\\
-2x+8y=+14
\\
—————-
\\
\hspace{9pt} 0x+11y=22
\end {cases}
\\[1cm]
\begin {cases}
y=\frac{22}{11}=2
\\[0.2cm]
x=\frac{8-3y}{2}=1
\end {cases}
\]
3.1.2 Igualació
Per tal d’aplicar el mètode d’igualació, aïllarem la mateixa incògnita de cada equació i després igualarem ambdues expressions.
\[\begin {cases}
2x+3y=8
\\
x-4y=-7
\end {cases}
\\[1cm]
\begin {cases}
x=\frac{8-3y}{2}
\\
x={-7+4y}
\end {cases}
\\[1.5cm]
\begin {cases}
\frac{8-3y}{2}={-7+4y}
\\[0.2cm]
(8-3y)=2*(-7+4y)
\\[0.2cm]
8-3y=-14+8y
\\[0.2cm]
-3y-8y=-14-8
\\[0.2cm]
-11y=-22
\\[0.2cm]
y=\frac{22}{11}=2
\end {cases}
\\[1cm]
\begin {cases}
x=\frac{8-3y}{2}=1
\end {cases}
\]
3.1.3 Substitució
En el mètode de substitució, aïllarem una de les incògnites i la substituirem a l’altra equació.
\[\begin {cases}
2x+3y=8
\\
x-4y=-7
\end {cases}
\\[1cm]
\begin {cases}
y=\frac{8-2x}{3}
\\[0.2cm]
x-4*(\frac{8-2x}{3})=-7
\\[0.2cm]
x-\frac{32-8x}{3}=-7
\\[0.2cm]
\frac{3x-32+8x}{3}=\frac{-21}{3}
\\[0.2cm]
3x+8x=-21+32
\\[0.2cm]
11x=11
\\[0.2cm]
x=1
\end {cases}
\\[1.5cm]
\begin {cases}
y=\frac{8-2x}{3}
\\[0.2cm]
y=2
\end {cases}
\]
3.1.4 Mètode gràfic
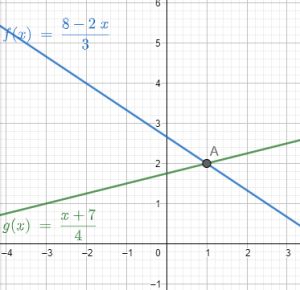
Aïllarem la \[y\] de cada equació i les representarem en un mateix gràfic.
Si el sistema és compatible determinat, el punt d’intersecció d’ambdues rectes serà la solució del sistema.
Si és indeterminat, ambdues rectes seran coincidents.
Si és incompatible, seran paral·leles.
3.2 No lineals
El millor mètode de resoldre sistemes d’equacions no lineals sol ser el mètode de substitució, tot i que s’ha d’analitzar en cada cas el sistema per a determinar quin és el millor métode de resolució.
Per a saber-me més, vegeu Altres mètodes de resolució d’equacions -Batxillerat).
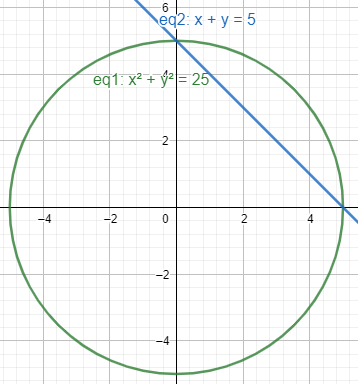
\[\begin {cases}
x^2+y^2=25
\\
x+y=5
\\
\end{cases}
\\[1cm]
\begin {cases}
x^2+y^2=25
\\
x=5-y
\\
\end{cases}
\\[1cm]
\begin {cases}
(5-y)^2+y^2=25
\\
(25-10y+y^2)+y^2=25
\\
2y^2-10y=0
\\
y*(2y-10)=0
\\
y=5, 0
\\
x=0, 5
\end{cases}
\]
4. De tres equacions amb tres incògnites
Per a resoldre un sistema de tres equacions amb tres incògnites, usarem el sistema de reducció entre la primera i la segona equació, després entre la primera i la tercera i finalment entres les dues equacions resultants:
\[2x+3y-z=4
\\
4x-2y+5z=7
\\
7x-5y+2z=4
\\[1cm]
*-2)2x+3y-\enspace z=4
\\
\hspace{1.2cm}4x-2y+5z=7
\\
———————–
\\
\hspace{1.2cm}0x+8y-7z=1
\\[1cm]
\hspace{0.5cm}7*) 2x+3y-\enspace z=4
\\
-2*)7x-5y+2z=4
\\
————————–
\\
\hspace{1.9cm}31y-11z=20
\\[1cm]
\hspace{0.2cm}31*) \hspace{0.3cm}8y-\enspace 7z=1
\\
-8*)31y-11z=20
\\
———————
\\
\hspace{1.2cm}-129z=-129
\\[1cm]
z=\frac{129}{129}=1
\\
y=\frac{1+7z}{8}=1
\\
x=\frac{4+z-3y}{2}=1
\]

 RSS CEEdukat
RSS CEEdukat

Quant a l'autor