Apèndix de cinemàtica

1. Cinemàtica relativista

En mecànica relativista, el temps i la distància depenen de l’observador que els mesuri.

1.1 Transformacions de Lorentz:

El 1881, els físics nord-americans Michelson i Morley mesuraren la velocitat de la llum en diferents direccions i, sorprenentment, trobaren que era sempre la mateixa. No obstant això, les transformacions de Galileu indiquen que cap objecte pot tenir la mateixa velocitat respecte a dos observadors que es mouen uniformement (MRU).

Einstein resolguí aquesta paradoxa el 1905 establint que la velocitat de la llum és la mateixa per a qualsevol observador. És a dir, que l’interval de temps que transcorre entre dos esdeveniments depèn de l’observador que el mesuri.

Per tant, s’han d’ajustar les transformacions de Galileu perquè la velocitat de la llum sigui invariant. Dos observadors (O i O’) que es mouen uniformement amb una velocitat relativa u respecte a l’eix X ajusten els rellotges perquè t=t’=0. Si en l’instant t=0, cada observador emet un raig de llum en direcció al punt A:

\begin{matrix} Per a cada observador es compleix que r^{2} = x^{2} + y^{2} + z^{2}, essent r = ct . Per tant, \\ {\begin{matrix} \begin{matrix} r = ct \to {(ct)}^{2} = x^{2} + y^{2} + z^{2} (1) \\ r = ct' \to {(ct')}^{2} = x'^{2} + y'^{2} + z'^{2} (2) \end{matrix} \end{matrix} \\ Subtituint les equacions de les transformacions de Galileu en l'equació del segon observador: \\ x' = x - ut; y' = y; z' = z; t' = t \to x^{2} + y^{2} + z^{2} - 2 xut + u^{2} t^{2} \\ Per tant, les Transformacions de Galileu ara no funcionen perquè no es compleix la igualtat. \\ El terme 2 xut + u^{2} t^{2} conté temps i espai. Si ajustem x' i t' per fer que les equacions (1) i (2) coincideixin: \\ x' = k (x - ut) i t' = a (t - bx) : \\ k^{2} (x^{2} - 2 uxt + u^{2} t^{2}) + y^{2} + z^{2} = c^{2} a^{2} (t^{2} - 2 bxt + b^{2} x^{2}) \\ (k^{2} - b^{2} a^{2} c^{2}) x^{2} - 2 (k^{2} u - b a^{2} c^{2}) xt + y^{2} + z^{2} = (a^{2} - k^{2} \frac{u^{2}}{c^{2}}) c^{2} t^{2} \\ k^{2} \to b^{2} a^{2} c^{2} = 1, k^{2} u - b a^{2} c^{2} = 0, a^{2} - k^{2} \frac{u^{2}}{c^{2}} = 1 \\ Per tant, \\ k = a = \frac{1}{\sqrt{1 - u^{2} / c^{2}}}, b = u / c^{2} \\ {\begin{matrix} \begin{matrix} x' = k (x - ut) = \frac{x - ut}{\sqrt{1 - u^{2} / c^{2}}} \end{matrix} \\ y' = y \\ z' = z \\ t' = a (t - bx) = \frac{t - ux / c^{2}}{\sqrt{1 - u^{2} / c^{2}}} \end{matrix} \\ L'expressió \frac{1}{\sqrt{1 - u^{2} / c^{2}}} és el factor de Lorentz \\ Quan u ≪ c, s'obtenen les transformacions de Galileu. \end{matrix}

1. 2 Transformacions de velocitat

\begin{matrix} v_{x} = \frac{dx}{dt}, v_{y} = \frac{dy}{dt}, v_{z} = \frac{dz}{dt} \\ v'_{x} = \frac{dx'}{dt'}, v'_{y} = \frac{dy'}{dt'}, v'_{z} = \frac{dz}{dt'} \\ {\begin{matrix} \begin{matrix} dx' = \frac{dx - u dt}{\sqrt{1 - u^{2} / c^{2}}} = \frac{v_{x} - u}{\sqrt{1 - u^{2} / c^{2}}} dt \\ dy' = dy \\ dz' = dz \\ dt' = \frac{dt - u dx / c ²}{\sqrt{1 - u^{2} / c^{2}}} \end{matrix} \end{matrix} \to {\begin{matrix} \begin{matrix} v'_{x} = \frac{dx'}{dt'} = \frac{v_{x} - u}{u - v_{x} / c^{2}} \\ v'_{y} = \frac{dy'}{dt'} = \frac{v_{y} \sqrt{1 - u^{2} / c^{2}}}{1 - u v_{x} / c^{2}} \\ v'_{z} = \frac{dz'}{dt'} = \frac{v_{z} \sqrt{1 - u^{2} / c^{2}}}{1 - u v_{x} / c^{2}} \end{matrix} \end{matrix} \end{matrix}

Si considerem que el moviment sols és en la direcció de l’eix \[X \] i anomenem \[v\] a \[v_x\]

v ’ = \frac{v_{x} - u}{u - v_{x} / c^{2}}, v ’_{y} = v ’_{z} = 0

1. 3 Conseqüències de les Transformacions de Lorentz

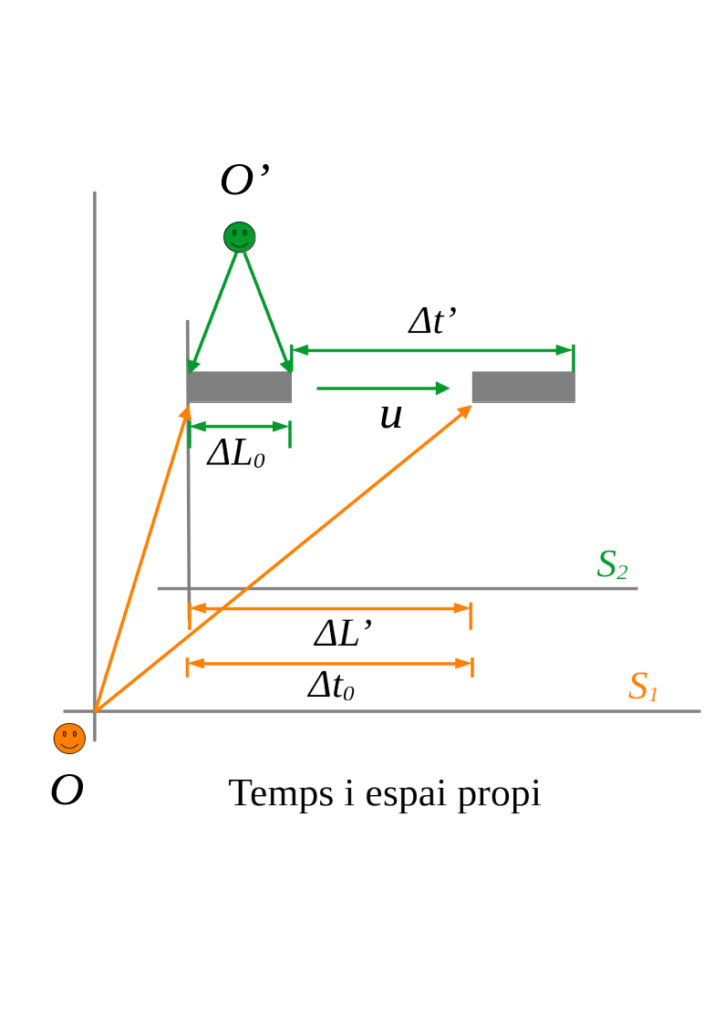
1.3.1 Temps i espai propi

Anomenem longitud pròpia \[L_0\] a la longitud mesurada per l’observador que és en el mateix sistema de referència que l’objecte. En aquest cas, l’observador i l’objecte tindran una velocitat relativa \[u=0.\]

Anomenem temps propi \[\tau, t_0\] a l’interval de temps que mesura l’observador pel qual dos esdeveniments ocorren en la mateixa posició.

La longitud o temps no propis els indiquem per L’, t’.

1.3.2 Contracció de la longitud

Per a fer la mesura de la longitud d’un objecte que és en MRU, l’observador en repòs ha d’emetre els dos rajos de llum simultàniament.

Per a un observador \[O’\], la longitud de la barra serà \[L’=x’_b-x’_a\]

Però, per a l’observador \[O\] la longitud serà \[L_0=x_b-x_a\]

\begin{matrix} x'_{a} = \frac{x_{a} - ut}{\sqrt{1 - u ² / c ²}}, x'_{b} = \frac{x_{b} - ut}{\sqrt{1 - u ² / c ²}} \to L' = \frac{x_{b} - x_{a}}{\sqrt{1 - u ² / c ²}} = \frac{L_{0}}{\sqrt{1 - u ² / c ²}} \\ L_{0} γ = L' \\ (L_{0} és la longitud pròpia i u és la velocitat relativa entre els observadors i c és la velocitat de la llum) \end{matrix}

Com que \[γ<0\], la longitud mesurada per l’observador \[O\], que veu la barra en moviment, és més petita que la mesurada per l’observador \[O’\], que veu l’objecte en repòs. És a dir, que els objectes en moviment semblen més curts.

1.3.3 Dilatació temporal

Si dos observadors en moviment relatiu mesuren la separació temporal entre dos esdeveniments, trobaran valors diferents. Considerant que un dels dos observadors mesura ambdós esdeveniments sense moure’s:

\begin{matrix} Δ t' = \frac{Δ t_{0}}{\sqrt{1 - {(u / c)}^{2}}} = Δ t_{0} \frac{1}{\sqrt{1 - β^{2}}} \\ Δ t' = \frac{Δ t_{0}}{γ} \end{matrix}

Apèndix de cinemàtica