Instruccions abans de començar
Els nombres reals és el conjunt de nombres format pel conjunt dels nombres racionals i el conjunt dels nombres irracionals.
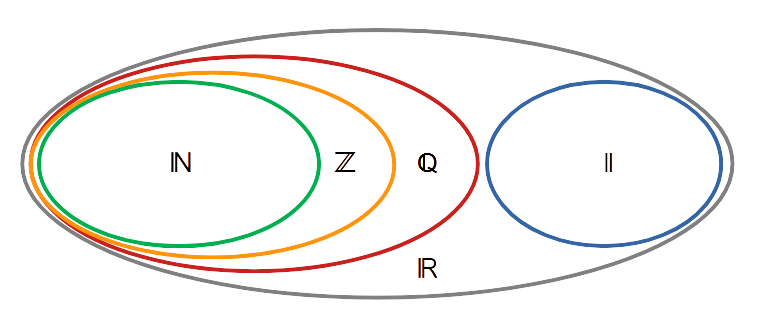
El nombres reals són un subconjunt de nombres complexos.
1. Nombres Naturals
Són els nombres que usem per a comptar: \(0, 1, 2, 3, 4, 5, … \). El conjunt dels nombres naturals es representa per \(\mathbb{N}\).
1.1 Nombres primers
Són els nombres naturals que sols són divisibles per ells mateixos i per la unitat.
Exemple:
\(2, 3, 5, 7, 11…\)
1.2 Nombres compostos
Un nombre compost, és un nombre format pel producte de nombres primers.
Exemple:
\(
6=2*3\\
24=2^3*3\\
60=2^2*5*3\\
450=2*3^2*5^2
\)
2. Nombres enters
És el conjunt dels nombres naturals positius, negatius i el 0: \(…-3,-2,-1,0,1,2,3,…\). El conjunt de nombres enters es representa per \(\mathbb{Z}\).
Els nombres naturals són part dels nombres enters (\(\mathbb{N} \subset \mathbb{Z}\)).
3. Nombres racionals
Són els nombres decimals generats per una fracció que anomenem fracció generatriu\( \frac{a}{b}\). \(a,b\) són nombres enters i \(b \neq 0\). Els conjunt de nombres racionals es representa per \(\mathbb{Q}\).
Exemple:
\(\frac{21}{10}=2.1, \, \frac{3}{2}=1.5\).
Els nombres enters també són racionals perquè els podem expressar en forma de fracció: \(2 = \frac{2}{1}\). Per tant, els nombres enters són un subconjunt dels racionals (\(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q}\)).
Els nombres decimals dels quals en podem trobar una fracció generatriu són:
3.1 Decimals exactes
Els decimals exactes són els nombres decimals que tenen una quantitat exacta de decimals.
Exemple:
\(2.345\), té tres decimals
\(0.9\), té un decimal
\(5.129837\), té sis decimals
Per a calcular la fracció generatriu d’un decimal exacte (\(2.345\)), fem el següent:
i) Escrivim el nombre sense comes al numerador: \(2\, 345\)
ii) El dividim per \(10 \) elevat al nombre de decimals que tingui: \(\frac{2\, 345}{10^3}=\frac{2\, 345}{1\, 000}\).
iii) Calculem la fracció irreductible: \(\frac{469}{200}…\)
Exemple:
\(1.75= \frac{175}{10^ 2} = \frac{7}{4}\).
3.2 Decimals periòdics purs
Els decimals periòdics purs són nombres amb decimals que es repeteixen indefinidament. Representem aquests decimals (període) amb un accent circumflex (^) al damunt.
Exemple:
\(
2.33333… \rightarrow 2. \hat 3 \\
0.66666… \rightarrow 0. \hat 6 \\
8.97979… \rightarrow 8. \widehat {97} \\
\)
Per a calcular la fracció generatriu dels nombres periòdics hem d’eliminar el període.
En en el cas dels periòdics purs, multipliquem en nombre per \(10\) elevat al nombre de decimals del període i al resultat li restem la part entera del nombre:
Exemple:
\(
n=56. \widehat{987} \\
1000*n= 56\, 987. \widehat{987}\\
n \hspace{1cm}= \hspace{0.8cm}56.\widehat{987}\\
999*n \hspace{0.2cm}=\hspace{0.2cm}56931.0\\
n=\frac{56931}{999}
\)
La forma ràpida de calcular la fracció generatriu és:
i) Escrivim al numerador la diferència entre el nombre sense coma i el nombre fins al període: \(56\, 987-56=56\, 931\)
ii) Escrivim al denominador tants 9 com decimals té el període: \(999\)
iii) Calculem al fracció irreductible: \(\frac{56\, 931}{999}=\frac{56\, 931}{999}\)
Exemple:
\(
1.23232323…= 1.\widehat {23} \\
\frac{123 – 1}{99} = \\
\frac{122}{99}
\)
En aquest exemple, el nombre sense la coma és \(123\), el període és \(\widehat{23}\), el nombre fins al període és l’\(1\) i el període té dos decimals.
3.3 Decimals periòdics mixts
Un nombre periòdic mixt, és un nombre amb una part dels decimals exacte i una altra de periòdica.
Per a calcular la fracció generatriu eliminem el període multiplicant el nombre decimal per \(10\) elevat al nombre de decimals i al resultat li restem el nombre format per la part entera i els decimals exactes:
Exemple
\(
n=56.9 \widehat{87} \\
1000*n= 56\, 987. \widehat{87}\\
-\\
10*n \hspace{0.4cm}=\hspace{0.6cm}569.\widehat{87}\\
———\\
990*n \hspace{0.4cm}=\, 56 \,418.0
\\
n=\frac{56\, 418}{990}
\)
Per a calcular la fracció generatriu, fem:
i) Escrivim al numerador la diferència entre el nombre sense coma i el nombre fins al període: \(56\, 987-569=56\, 418\)
ii) Escrivim al denominador tants 9 com decimals té el període i tants zeros com decimals tingui l’avantperíode: \(990\)
iii) Calculem al fracció irreductible: \(\frac{56\, 418}{900}=\frac{9\, 403}{150}\)
Exemple:
\(1.5787878…= 1.5\widehat{78} = \\
\frac{157 – 15}{900} =\\
\frac{142}{900} = \\
\frac{71}{450}
\)
En aquest exemple, el nombre sense la coma és \(1578\), l’avantperíode és \(5\) i el període és \(\widehat 78\) i el nombre fins al període és l’\(1\). L’avantperíode té un decimal exacte i el període dos.
4. Nombres irracionals
Són els decimals infinits no periòdics. Com que no podem trobar-ne la fracció generatriu, no són racionals. Els conjunt de nombres irracionals es representa per \(\mathbb{I}\).
Exemple:
\(\pi, e\), qualsevol arrel no exacta com \(\sqrt{2}, \sqrt{5}, \sqrt{1.34}\).
5. Nombres reals
És el conjunt de nombres racionals i els irracionals. El conjunt de nombres reals es representa per \(\mathbb{R}\).
Per tant, \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}, \mathbb{I} \subset \mathbb{R}\).
Els nombres reals es representen a la recta real.
5.1 Representació a la recta real
i) Per a representar un nombre enter (\(\mathbb{Z}\)) a la recta real, la dividim en dues parts i a la dreta hi coloquem el nombre enters positius (\(\mathbb{N}\)) i a l’esquerra en negatius:
ii) Per a representar un nombre racional (\(\mathbb{Q}\)), primer calcularem la fracció generatriu i després la representaren a la recta real.
Les fraccions poden ser pròpies o impròpies:
En una fracció pròpia, el numerador és més petit que el denominador i, per tant, el nombre decimal serà un nombre entre \(0\) i \(1\) (p.e: \(\frac{4}{5}=0.8\)).
En una fracció impròpia, el numerador és més gran que el denominador i, per tant, el resultat és més gran que u (p.e \(\frac{5}{2}=2.5)\). Les fraccions impròpies són els nombre mixtos (\(\frac{5}{2}=2+\frac{1}{2}\)).
Exemple:
Calculem la fracció (pròpia) generatriu:
\(
0.75=\frac{75}{100}=\frac{3}{4}
\)
Per a representar la fracció (pròpia) a la recta real:
i) Dibuixem una línia qualsevol i la dividem en tantes parts iguals com indiqui el denominador, unim el darrer punt amb l’u i tracem paral·leles des de cada punt fins que tallin la recta real per tal de dividir el segment \( 0-1\) en parts iguals.
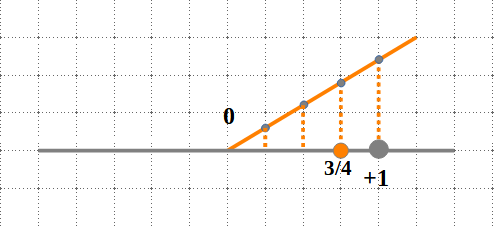
Si la fracció generatriu és impròpia, usarem el matexi procediment:
Exemple:
\(
1.75=\frac{175}{100}=\frac{7}{4}=2+\frac{3}{4}
\)
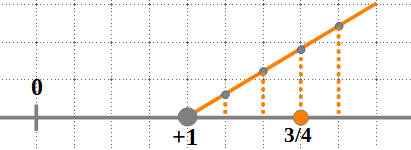
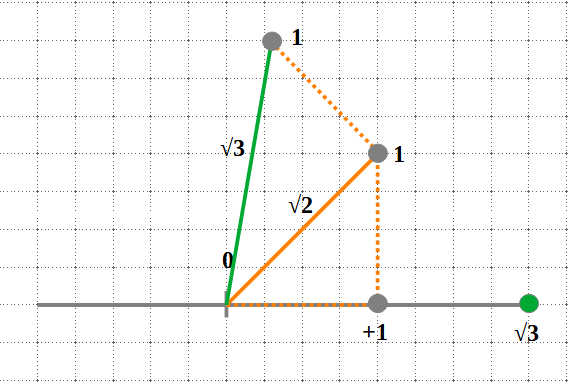
iii) Per a representar un nombre irracional, farem servir el Teorema de Pitàgores:
Exemple:
\(
\sqrt{2}=\sqrt{1^2+1^2}
\\
\sqrt{3}=\sqrt{(\sqrt{2})^2+1^2}
\)
6. Intervals
És un segment de la recta real que obtenim quan la fitem per dos extrems. L’extrem de l’esquerra és l’extrem inferior i el de la dreta el superior. La diferència entre els dos extrems és l’amplitud de l’interval.
Un extrem és obert quan format no part de l’interval i tancat si en forma part. Un interval amb els dos extrems oberts és un interval obert. Si té un extrem obert i l’altra tancat és un interval semiobert i si tots dos són tancats és un interval tancat.
Exemple:
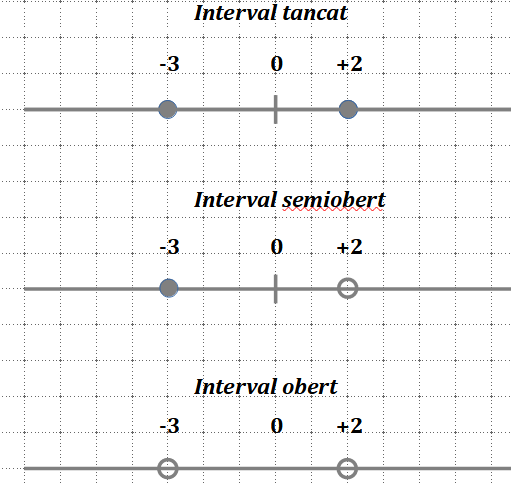
Escriurem els intervals anteriors amb notació algebraica de la següents forma:
\(-3\leq x\leq +2,\, -3\leq x \lt +2,\, -3\lt x\lt +2\). En una semirecta, l’extrem infinit sempre és un extrem obert (p.e, \((- \infty \lt x \leq +2]\)).
Escriurem els intervals anteriors amb notació d’interval de la següents forma:
\(\left[ -3,+2\right], \, \left] -3,+2\right], \left] -3,+2\right[\). \( ]n , n[\) o bé \((n , n)\) significa que l’extrem és obert i \( [n , n] \) vol dir que l’extrem és tancat. En una semirecta, un extrem és obert i l’altre tancat: \((-\infty, +2]\)).
7. Notació científica
És un nombre expressat segons la notació \(N*10^a\). \(N\) és un nombre decimal amb la part entera d’un sol dígit diferent de zero i \(a\) és un nombre enter.
Usem la notació científica per a expressar d’una manera més entenedora els nombres molt grans o molt petits.
Exemple:
\(
1 236 598 485 963=\, 1.236598485963*10^{+12} \\
0.0000000002568=\, 2.568*10^{-9}
\)
En el primer cas, hem desplaçat la coma 12 posicions cap a l’esquerra, és a dir, hem dividit el nombre per \(10^{-12}\). Per tant, per a mantenir l’equivalència del nombre, l’hem multiplicat per \(10^{+12}\).
En el segon cas, hem desplaçat la coma 9 posicions cap a la dreta, és a dir, hem multiplicat el nombre per \(10^{+9}\). Per tant, per a mantenir l’equivalència del nombre, l’hem dividit per \(10^{-9}\).
7.1 Operacions
Per a multiplicar o dividir dos nombres en notació científica, multipliquem o dividim els nombres i les potències de deu. Si el resultat no té la forma de notació científica, el transformarem perquè la tingui.
Exemple:
\(
2.56 10^{+5}*3.72 10^{-3}=\\
(2.56*3.72)*(10^{+5}*10^{-3})=\
9.4116*10^{+2}
\)
Per a sumar o restar nombre en notació científica, les potències de deu han de tenir el mateix exponent. Si l’exponent no és igual, transformarem un dels dos nombres perquè ho siguin.
Exemple:
\(
2.56 10^{+5}+3.72 10^{-3}=\\
(256 000 000 10^{-3}+3.72 10^{-3}=\\
256000003.7 10^{-3}=\\
2.560000037 10^{5}
\)
Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons
Un nombre compost, és un nombre format pel producte de nombres primers.
Exemple:
\(6=2*3\\
24=2^3*3\\
60=2^2*5*3\\
450=2*3^2*5^2
\)
2. Nombres enters
És el conjunt dels nombres naturals positius, negatius i el 0: \(…-3,-2,-1,0,1,2,3,…\). El conjunt de nombres enters es representa per \(\mathbb{Z}\).
Els nombres naturals són part dels nombres enters (\(\mathbb{N} \subset \mathbb{Z}\)).
3. Nombres racionals
Són els nombres decimals generats per una fracció que anomenem fracció generatriu\( \frac{a}{b}\). \(a,b\) són nombres enters i \(b \neq 0\). Els conjunt de nombres racionals es representa per \(\mathbb{Q}\).
Exemple:
\(\frac{21}{10}=2.1, \, \frac{3}{2}=1.5\).
Els nombres enters també són racionals perquè els podem expressar en forma de fracció: \(2 = \frac{2}{1}\). Per tant, els nombres enters són un subconjunt dels racionals (\(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q}\)).
Els nombres decimals dels quals en podem trobar una fracció generatriu són:
3.1 Decimals exactes
Els decimals exactes són els nombres decimals que tenen una quantitat exacta de decimals.
Exemple:
\(2.345\), té tres decimals
\(0.9\), té un decimal
\(5.129837\), té sis decimals
Per a calcular la fracció generatriu d’un decimal exacte (\(2.345\)), fem el següent:
i) Escrivim el nombre sense comes al numerador: \(2\, 345\)
ii) El dividim per \(10 \) elevat al nombre de decimals que tingui: \(\frac{2\, 345}{10^3}=\frac{2\, 345}{1\, 000}\).
iii) Calculem la fracció irreductible: \(\frac{469}{200}…\)
Exemple:
\(1.75= \frac{175}{10^ 2} = \frac{7}{4}\).
3.2 Decimals periòdics purs
Els decimals periòdics purs són nombres amb decimals que es repeteixen indefinidament. Representem aquests decimals (període) amb un accent circumflex (^) al damunt.
Exemple:
\(
2.33333… \rightarrow 2. \hat 3 \\
0.66666… \rightarrow 0. \hat 6 \\
8.97979… \rightarrow 8. \widehat {97} \\
\)
Per a calcular la fracció generatriu dels nombres periòdics hem d’eliminar el període.
En en el cas dels periòdics purs, multipliquem en nombre per \(10\) elevat al nombre de decimals del període i al resultat li restem la part entera del nombre:
Exemple:
\(
n=56. \widehat{987} \\
1000*n= 56\, 987. \widehat{987}\\
n \hspace{1cm}= \hspace{0.8cm}56.\widehat{987}\\
999*n \hspace{0.2cm}=\hspace{0.2cm}56931.0\\
n=\frac{56931}{999}
\)
La forma ràpida de calcular la fracció generatriu és:
i) Escrivim al numerador la diferència entre el nombre sense coma i el nombre fins al període: \(56\, 987-56=56\, 931\)
ii) Escrivim al denominador tants 9 com decimals té el període: \(999\)
iii) Calculem al fracció irreductible: \(\frac{56\, 931}{999}=\frac{56\, 931}{999}\)
Exemple:
\(
1.23232323…= 1.\widehat {23} \\
\frac{123 – 1}{99} = \\
\frac{122}{99}
\)
En aquest exemple, el nombre sense la coma és \(123\), el període és \(\widehat{23}\), el nombre fins al període és l’\(1\) i el període té dos decimals.
3.3 Decimals periòdics mixts
Un nombre periòdic mixt, és un nombre amb una part dels decimals exacte i una altra de periòdica.
Per a calcular la fracció generatriu eliminem el període multiplicant el nombre decimal per \(10\) elevat al nombre de decimals i al resultat li restem el nombre format per la part entera i els decimals exactes:
Exemple
\(
n=56.9 \widehat{87} \\
1000*n= 56\, 987. \widehat{87}\\
-\\
10*n \hspace{0.4cm}=\hspace{0.6cm}569.\widehat{87}\\
———\\
990*n \hspace{0.4cm}=\, 56 \,418.0
\\
n=\frac{56\, 418}{990}
\)
Per a calcular la fracció generatriu, fem:
i) Escrivim al numerador la diferència entre el nombre sense coma i el nombre fins al període: \(56\, 987-569=56\, 418\)
ii) Escrivim al denominador tants 9 com decimals té el període i tants zeros com decimals tingui l’avantperíode: \(990\)
iii) Calculem al fracció irreductible: \(\frac{56\, 418}{900}=\frac{9\, 403}{150}\)
Exemple:
\(1.5787878…= 1.5\widehat{78} = \\
\frac{157 – 15}{900} =\\
\frac{142}{900} = \\
\frac{71}{450}
\)
En aquest exemple, el nombre sense la coma és \(1578\), l’avantperíode és \(5\) i el període és \(\widehat 78\) i el nombre fins al període és l’\(1\). L’avantperíode té un decimal exacte i el període dos.
4. Nombres irracionals
Són els decimals infinits no periòdics. Com que no podem trobar-ne la fracció generatriu, no són racionals. Els conjunt de nombres irracionals es representa per \(\mathbb{I}\).
Exemple:
\(\pi, e\), qualsevol arrel no exacta com \(\sqrt{2}, \sqrt{5}, \sqrt{1.34}\).
5. Nombres reals
És el conjunt de nombres racionals i els irracionals. El conjunt de nombres reals es representa per \(\mathbb{R}\).
Per tant, \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}, \mathbb{I} \subset \mathbb{R}\).
Els nombres reals es representen a la recta real.
5.1 Representació a la recta real
i) Per a representar un nombre enter (\(\mathbb{Z}\)) a la recta real, la dividim en dues parts i a la dreta hi coloquem el nombre enters positius (\(\mathbb{N}\)) i a l’esquerra en negatius:
ii) Per a representar un nombre racional (\(\mathbb{Q}\)), primer calcularem la fracció generatriu i després la representaren a la recta real.
Les fraccions poden ser pròpies o impròpies:
En una fracció pròpia, el numerador és més petit que el denominador i, per tant, el nombre decimal serà un nombre entre \(0\) i \(1\) (p.e: \(\frac{4}{5}=0.8\)).
En una fracció impròpia, el numerador és més gran que el denominador i, per tant, el resultat és més gran que u (p.e \(\frac{5}{2}=2.5)\). Les fraccions impròpies són els nombre mixtos (\(\frac{5}{2}=2+\frac{1}{2}\)).
Exemple:
Calculem la fracció (pròpia) generatriu:
\(
0.75=\frac{75}{100}=\frac{3}{4}
\)
Per a representar la fracció (pròpia) a la recta real:
i) Dibuixem una línia qualsevol i la dividem en tantes parts iguals com indiqui el denominador, unim el darrer punt amb l’u i tracem paral·leles des de cada punt fins que tallin la recta real per tal de dividir el segment \( 0-1\) en parts iguals.
Si la fracció generatriu és impròpia, usarem el matexi procediment:
Exemple:
\(
1.75=\frac{175}{100}=\frac{7}{4}=2+\frac{3}{4}
\)
iii) Per a representar un nombre irracional, farem servir el Teorema de Pitàgores:
Exemple:
\(
\sqrt{2}=\sqrt{1^2+1^2}
\\
\sqrt{3}=\sqrt{(\sqrt{2})^2+1^2}
\)
6. Intervals
És un segment de la recta real que obtenim quan la fitem per dos extrems. L’extrem de l’esquerra és l’extrem inferior i el de la dreta el superior. La diferència entre els dos extrems és l’amplitud de l’interval.
Un extrem és obert quan format no part de l’interval i tancat si en forma part. Un interval amb els dos extrems oberts és un interval obert. Si té un extrem obert i l’altra tancat és un interval semiobert i si tots dos són tancats és un interval tancat.
Exemple:
Escriurem els intervals anteriors amb notació algebraica de la següents forma:
\(-3\leq x\leq +2,\, -3\leq x \lt +2,\, -3\lt x\lt +2\). En una semirecta, l’extrem infinit sempre és un extrem obert (p.e, \((- \infty \lt x \leq +2]\)).
Escriurem els intervals anteriors amb notació d’interval de la següents forma:
\(\left[ -3,+2\right], \, \left] -3,+2\right], \left] -3,+2\right[\). \( ]n , n[\) o bé \((n , n)\) significa que l’extrem és obert i \( [n , n] \) vol dir que l’extrem és tancat. En una semirecta, un extrem és obert i l’altre tancat: \((-\infty, +2]\)).
7. Notació científica
És un nombre expressat segons la notació \(N*10^a\). \(N\) és un nombre decimal amb la part entera d’un sol dígit diferent de zero i \(a\) és un nombre enter.
Usem la notació científica per a expressar d’una manera més entenedora els nombres molt grans o molt petits.
Exemple:
\(
1 236 598 485 963=\, 1.236598485963*10^{+12} \\
0.0000000002568=\, 2.568*10^{-9}
\)
En el primer cas, hem desplaçat la coma 12 posicions cap a l’esquerra, és a dir, hem dividit el nombre per \(10^{-12}\). Per tant, per a mantenir l’equivalència del nombre, l’hem multiplicat per \(10^{+12}\).
En el segon cas, hem desplaçat la coma 9 posicions cap a la dreta, és a dir, hem multiplicat el nombre per \(10^{+9}\). Per tant, per a mantenir l’equivalència del nombre, l’hem dividit per \(10^{-9}\).
7.1 Operacions
Per a multiplicar o dividir dos nombres en notació científica, multipliquem o dividim els nombres i les potències de deu. Si el resultat no té la forma de notació científica, el transformarem perquè la tingui.
Exemple:
\(
2.56 10^{+5}*3.72 10^{-3}=\\
(2.56*3.72)*(10^{+5}*10^{-3})=\
9.4116*10^{+2}
\)
Per a sumar o restar nombre en notació científica, les potències de deu han de tenir el mateix exponent. Si l’exponent no és igual, transformarem un dels dos nombres perquè ho siguin.
Exemple:
\(
2.56 10^{+5}+3.72 10^{-3}=\\
(256 000 000 10^{-3}+3.72 10^{-3}=\\
256000003.7 10^{-3}=\\
2.560000037 10^{5}
\)
Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons
\(0.9\), té un decimal
\(5.129837\), té sis decimals
Els decimals periòdics purs són nombres amb decimals que es repeteixen indefinidament. Representem aquests decimals (període) amb un accent circumflex (^) al damunt.
Exemple:
\(2.33333… \rightarrow 2. \hat 3 \\
0.66666… \rightarrow 0. \hat 6 \\
8.97979… \rightarrow 8. \widehat {97} \\
\)
Per a calcular la fracció generatriu dels nombres periòdics hem d’eliminar el període.
En en el cas dels periòdics purs, multipliquem en nombre per \(10\) elevat al nombre de decimals del període i al resultat li restem la part entera del nombre:
Exemple:
\(n=56. \widehat{987} \\
1000*n= 56\, 987. \widehat{987}\\
n \hspace{1cm}= \hspace{0.8cm}56.\widehat{987}\\
999*n \hspace{0.2cm}=\hspace{0.2cm}56931.0\\
n=\frac{56931}{999}
\)
La forma ràpida de calcular la fracció generatriu és:
i) Escrivim al numerador la diferència entre el nombre sense coma i el nombre fins al període: \(56\, 987-56=56\, 931\)
ii) Escrivim al denominador tants 9 com decimals té el període: \(999\)
iii) Calculem al fracció irreductible: \(\frac{56\, 931}{999}=\frac{56\, 931}{999}\)
Exemple:
\(1.23232323…= 1.\widehat {23} \\
\frac{123 – 1}{99} = \\
\frac{122}{99}
\)
En aquest exemple, el nombre sense la coma és \(123\), el període és \(\widehat{23}\), el nombre fins al període és l’\(1\) i el període té dos decimals.
3.3 Decimals periòdics mixts
Un nombre periòdic mixt, és un nombre amb una part dels decimals exacte i una altra de periòdica.
Per a calcular la fracció generatriu eliminem el període multiplicant el nombre decimal per \(10\) elevat al nombre de decimals i al resultat li restem el nombre format per la part entera i els decimals exactes:
Exemple
\(
n=56.9 \widehat{87} \\
1000*n= 56\, 987. \widehat{87}\\
-\\
10*n \hspace{0.4cm}=\hspace{0.6cm}569.\widehat{87}\\
———\\
990*n \hspace{0.4cm}=\, 56 \,418.0
\\
n=\frac{56\, 418}{990}
\)
Per a calcular la fracció generatriu, fem:
i) Escrivim al numerador la diferència entre el nombre sense coma i el nombre fins al període: \(56\, 987-569=56\, 418\)
ii) Escrivim al denominador tants 9 com decimals té el període i tants zeros com decimals tingui l’avantperíode: \(990\)
iii) Calculem al fracció irreductible: \(\frac{56\, 418}{900}=\frac{9\, 403}{150}\)
Exemple:
\(1.5787878…= 1.5\widehat{78} = \\
\frac{157 – 15}{900} =\\
\frac{142}{900} = \\
\frac{71}{450}
\)
En aquest exemple, el nombre sense la coma és \(1578\), l’avantperíode és \(5\) i el període és \(\widehat 78\) i el nombre fins al període és l’\(1\). L’avantperíode té un decimal exacte i el període dos.
4. Nombres irracionals
Són els decimals infinits no periòdics. Com que no podem trobar-ne la fracció generatriu, no són racionals. Els conjunt de nombres irracionals es representa per \(\mathbb{I}\).
Exemple:
\(\pi, e\), qualsevol arrel no exacta com \(\sqrt{2}, \sqrt{5}, \sqrt{1.34}\).
5. Nombres reals
És el conjunt de nombres racionals i els irracionals. El conjunt de nombres reals es representa per \(\mathbb{R}\).
Per tant, \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}, \mathbb{I} \subset \mathbb{R}\).
Els nombres reals es representen a la recta real.
5.1 Representació a la recta real
i) Per a representar un nombre enter (\(\mathbb{Z}\)) a la recta real, la dividim en dues parts i a la dreta hi coloquem el nombre enters positius (\(\mathbb{N}\)) i a l’esquerra en negatius:
ii) Per a representar un nombre racional (\(\mathbb{Q}\)), primer calcularem la fracció generatriu i després la representaren a la recta real.
Les fraccions poden ser pròpies o impròpies:
En una fracció pròpia, el numerador és més petit que el denominador i, per tant, el nombre decimal serà un nombre entre \(0\) i \(1\) (p.e: \(\frac{4}{5}=0.8\)).
En una fracció impròpia, el numerador és més gran que el denominador i, per tant, el resultat és més gran que u (p.e \(\frac{5}{2}=2.5)\). Les fraccions impròpies són els nombre mixtos (\(\frac{5}{2}=2+\frac{1}{2}\)).
Exemple:
Calculem la fracció (pròpia) generatriu:
\(
0.75=\frac{75}{100}=\frac{3}{4}
\)
Per a representar la fracció (pròpia) a la recta real:
i) Dibuixem una línia qualsevol i la dividem en tantes parts iguals com indiqui el denominador, unim el darrer punt amb l’u i tracem paral·leles des de cada punt fins que tallin la recta real per tal de dividir el segment \( 0-1\) en parts iguals.
Si la fracció generatriu és impròpia, usarem el matexi procediment:
Exemple:
\(
1.75=\frac{175}{100}=\frac{7}{4}=2+\frac{3}{4}
\)
iii) Per a representar un nombre irracional, farem servir el Teorema de Pitàgores:
Exemple:
\(
\sqrt{2}=\sqrt{1^2+1^2}
\\
\sqrt{3}=\sqrt{(\sqrt{2})^2+1^2}
\)
6. Intervals
És un segment de la recta real que obtenim quan la fitem per dos extrems. L’extrem de l’esquerra és l’extrem inferior i el de la dreta el superior. La diferència entre els dos extrems és l’amplitud de l’interval.
Un extrem és obert quan format no part de l’interval i tancat si en forma part. Un interval amb els dos extrems oberts és un interval obert. Si té un extrem obert i l’altra tancat és un interval semiobert i si tots dos són tancats és un interval tancat.
Exemple:
Escriurem els intervals anteriors amb notació algebraica de la següents forma:
\(-3\leq x\leq +2,\, -3\leq x \lt +2,\, -3\lt x\lt +2\). En una semirecta, l’extrem infinit sempre és un extrem obert (p.e, \((- \infty \lt x \leq +2]\)).
Escriurem els intervals anteriors amb notació d’interval de la següents forma:
\(\left[ -3,+2\right], \, \left] -3,+2\right], \left] -3,+2\right[\). \( ]n , n[\) o bé \((n , n)\) significa que l’extrem és obert i \( [n , n] \) vol dir que l’extrem és tancat. En una semirecta, un extrem és obert i l’altre tancat: \((-\infty, +2]\)).
7. Notació científica
És un nombre expressat segons la notació \(N*10^a\). \(N\) és un nombre decimal amb la part entera d’un sol dígit diferent de zero i \(a\) és un nombre enter.
Usem la notació científica per a expressar d’una manera més entenedora els nombres molt grans o molt petits.
Exemple:
\(
1 236 598 485 963=\, 1.236598485963*10^{+12} \\
0.0000000002568=\, 2.568*10^{-9}
\)
En el primer cas, hem desplaçat la coma 12 posicions cap a l’esquerra, és a dir, hem dividit el nombre per \(10^{-12}\). Per tant, per a mantenir l’equivalència del nombre, l’hem multiplicat per \(10^{+12}\).
En el segon cas, hem desplaçat la coma 9 posicions cap a la dreta, és a dir, hem multiplicat el nombre per \(10^{+9}\). Per tant, per a mantenir l’equivalència del nombre, l’hem dividit per \(10^{-9}\).
7.1 Operacions
Per a multiplicar o dividir dos nombres en notació científica, multipliquem o dividim els nombres i les potències de deu. Si el resultat no té la forma de notació científica, el transformarem perquè la tingui.
Exemple:
\(
2.56 10^{+5}*3.72 10^{-3}=\\
(2.56*3.72)*(10^{+5}*10^{-3})=\
9.4116*10^{+2}
\)
Per a sumar o restar nombre en notació científica, les potències de deu han de tenir el mateix exponent. Si l’exponent no és igual, transformarem un dels dos nombres perquè ho siguin.
Exemple:
\(
2.56 10^{+5}+3.72 10^{-3}=\\
(256 000 000 10^{-3}+3.72 10^{-3}=\\
256000003.7 10^{-3}=\\
2.560000037 10^{5}
\)
Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons
i) Per a representar un nombre enter (\(\mathbb{Z}\)) a la recta real, la dividim en dues parts i a la dreta hi coloquem el nombre enters positius (\(\mathbb{N}\)) i a l’esquerra en negatius:
ii) Per a representar un nombre racional (\(\mathbb{Q}\)), primer calcularem la fracció generatriu i després la representaren a la recta real.
Les fraccions poden ser pròpies o impròpies:
En una fracció pròpia, el numerador és més petit que el denominador i, per tant, el nombre decimal serà un nombre entre \(0\) i \(1\) (p.e: \(\frac{4}{5}=0.8\)).
En una fracció impròpia, el numerador és més gran que el denominador i, per tant, el resultat és més gran que u (p.e \(\frac{5}{2}=2.5)\). Les fraccions impròpies són els nombre mixtos (\(\frac{5}{2}=2+\frac{1}{2}\)).
Exemple:
Calculem la fracció (pròpia) generatriu:
\(0.75=\frac{75}{100}=\frac{3}{4}
\)
Per a representar la fracció (pròpia) a la recta real:
i) Dibuixem una línia qualsevol i la dividem en tantes parts iguals com indiqui el denominador, unim el darrer punt amb l’u i tracem paral·leles des de cada punt fins que tallin la recta real per tal de dividir el segment \( 0-1\) en parts iguals.
Si la fracció generatriu és impròpia, usarem el matexi procediment:
Exemple:
\(1.75=\frac{175}{100}=\frac{7}{4}=2+\frac{3}{4}
\)
iii) Per a representar un nombre irracional, farem servir el Teorema de Pitàgores:
Exemple:
\(\sqrt{2}=\sqrt{1^2+1^2}
\\
\sqrt{3}=\sqrt{(\sqrt{2})^2+1^2}
\)
6. Intervals
És un segment de la recta real que obtenim quan la fitem per dos extrems. L’extrem de l’esquerra és l’extrem inferior i el de la dreta el superior. La diferència entre els dos extrems és l’amplitud de l’interval.
Un extrem és obert quan format no part de l’interval i tancat si en forma part. Un interval amb els dos extrems oberts és un interval obert. Si té un extrem obert i l’altra tancat és un interval semiobert i si tots dos són tancats és un interval tancat.
Exemple:
Escriurem els intervals anteriors amb notació algebraica de la següents forma:
\(-3\leq x\leq +2,\, -3\leq x \lt +2,\, -3\lt x\lt +2\). En una semirecta, l’extrem infinit sempre és un extrem obert (p.e, \((- \infty \lt x \leq +2]\)).
Escriurem els intervals anteriors amb notació d’interval de la següents forma:
\(\left[ -3,+2\right], \, \left] -3,+2\right], \left] -3,+2\right[\). \( ]n , n[\) o bé \((n , n)\) significa que l’extrem és obert i \( [n , n] \) vol dir que l’extrem és tancat. En una semirecta, un extrem és obert i l’altre tancat: \((-\infty, +2]\)).
7. Notació científica
És un nombre expressat segons la notació \(N*10^a\). \(N\) és un nombre decimal amb la part entera d’un sol dígit diferent de zero i \(a\) és un nombre enter.
Usem la notació científica per a expressar d’una manera més entenedora els nombres molt grans o molt petits.
Exemple:
\(1 236 598 485 963=\, 1.236598485963*10^{+12} \\
0.0000000002568=\, 2.568*10^{-9}
\)
En el primer cas, hem desplaçat la coma 12 posicions cap a l’esquerra, és a dir, hem dividit el nombre per \(10^{-12}\). Per tant, per a mantenir l’equivalència del nombre, l’hem multiplicat per \(10^{+12}\).
En el segon cas, hem desplaçat la coma 9 posicions cap a la dreta, és a dir, hem multiplicat el nombre per \(10^{+9}\). Per tant, per a mantenir l’equivalència del nombre, l’hem dividit per \(10^{-9}\).
7.1 Operacions
Per a multiplicar o dividir dos nombres en notació científica, multipliquem o dividim els nombres i les potències de deu. Si el resultat no té la forma de notació científica, el transformarem perquè la tingui.
Exemple:
\(
2.56 10^{+5}*3.72 10^{-3}=\\
(2.56*3.72)*(10^{+5}*10^{-3})=\
9.4116*10^{+2}
\)
Per a sumar o restar nombre en notació científica, les potències de deu han de tenir el mateix exponent. Si l’exponent no és igual, transformarem un dels dos nombres perquè ho siguin.
Exemple:
\(2.56 10^{+5}+3.72 10^{-3}=\\
(256 000 000 10^{-3}+3.72 10^{-3}=\\
256000003.7 10^{-3}=\\
2.560000037 10^{5}
\)
Aquesta obra està subjecta a una llicència de Reconeixement-NoComercial-Compartir Igual 4.0 Internacional de Creative Commons
RSS CEEdukat
