1. Definició
La integració (antiderivada) és el càlcul de la funció primitiva \(F(x)\) d’una funció \(f(x)\) . Si \(f(x)=F'(x) \Rightarrow \int f(x) \; dx=F(x)\).
La integració i la derivació són funcions inverses.
1.1 Propietats de les integrals
Si \( f(x)\) és la funció derivada d’una funció primitiva \( F(x)\):
1.1.1 \(\int {k \cdot f(x) \;dx}= k \cdot \int{f(x) \;dx}\)
1.1.2 \(\int {f(x)+g(x)\;dx}= \int{f(x) \;dx+\int{g(x) \;dx}}\)
1.1.3 \(\int {d[f(x)]}= f(x)\)
2. Integrals indefinides
Una integral indefinida són totes les funcions primitives \(F(x)\) d’una funció \(f(x):\) \(\int f(x) \enspace dx=F(x)+C\). Les diferents funcions es diferencien una de l ‘altra tan sols per un paràmetre \(C\).
Exemple:
\(F(x)=6x³-2x²+7x+8\\
f(x)=18x²-4x+7\\
F(x)=\int f(x) \; dx=\int (18x²-4x+7) \enspace dx=6x³-2x²+7x+C
\)
A la integral d’una funció derivada (primitiva) li hem d’afegir una constant \(C\) perquè la derivada d’una constant és zero, i quan derivem la primitiva aquesta constant es perd. Aquest paràmetre és el deplaçament vertical de la funció.
3. Integrals immediates
Són les integrals que s’obtenen de les regles de derivació invertides:
Exemple:
\(F(x)=x^n\\
f(x)=\frac{d[F(x)]}{dx}=\frac{d}{dx}x^n=n \cdot x^{n-1}\\
d[F(x)]=f(x) \; dx=n \cdot x^{n-1} \; dx\\[0.5cm]
\text{Per tant}:\\[0.5cm]
F(x)=\int {f(x) \; dx}=n \, \int {x^{n-1}} \enspace dx=x^n+C
\)
Les integrals obtingudes d’aquesta manera formen la taula d’integrals.
3.1 Taula d’integrals immediates
| f (x) | f(u) | F(x) | F(u) |
| \(\int dx\enspace\) | \(\int du\) | \(x+C\) | \(u+C\) |
| \(\int k \enspace dx\) | \(\int k \enspace du\) | \(kx+C\) | \(ku+C\) |
| \(\int {\frac{dx}{x}} \enspace dx\) | \(\int {\frac{du}{u}} \enspace dx\) | \(\ln x+C\) | \(\ln u+C\) |
| \(\int e^x \enspace dx\) | \(\int e^u \enspace du\) | \(e^x+C\) | \(e^u+C\) |
| \(\int a^x \enspace dx\) | \(\int a^u \enspace du\) | \(\frac{a^x}{\ln a}+C\) | \(\frac{a^u}{\ln a}+C\) |
| \(\int \sin x \enspace dx\) | \(\int \sin u \enspace du\) | \(-\cos x+C\) | \(-\cos u+C\) |
| \(\int \cos x \enspace dx\) | \(\int \cos u \enspace du\) | \(\sin x+C\) | \(\sin u+C\) |
| \(\int \tan x \enspace dx\) | \(\int \tan u \enspace du\) | \(-\ln |\cos x |+C\) | \(-\ln |\cos u |+C\) |
| \(\int \frac{1}{\sqrt{1-x²}} \enspace dx\) | \(\int \frac{1}{\sqrt{1-u²}} \enspace du\) | \(\arcsin x+C\) | \(\arcsin u+C\) |
| \(\int \frac{-1}{\sqrt{1-x²}} \enspace dx\) | \(\int \frac{-1}{\sqrt{1-u²}} \enspace du\) | \(\arccos x+C\) | \(\arccos u+C\) |
| \(\int \frac{1}{1+x²} \enspace dx\) | \(\int \frac{1}{1+u²} \enspace du\) | \(\arctan x+C\) | \(\arctan u+C\) |
La resolució és immediata, la integral d’una de les funcions derivades de la columna esquerra és la funció primitiva que li correspon de la columna de la dreta.
Per la regla de la cadena de derivació de funcions compostes, la integral ha d’encloure \(du\) la derivada d’ \(u\):
\(F(x)=e^{2x²+3x} \rightarrow F'(x)=f(x) \; dx=e^{2x²+3x} \cdot (4x+3) \; dx\\
\int {f(x) \; dx}=\int {e^{2x²+3x} \; (4x+3) \; dx}\\
[u=2x²+3x, \; du=(4x+3) \; dx]\\
\int {e^{2x²+3x} \; (4x+3) \; dx}= \int e^u \; du
\)
4. Mètodes d’integració
Si hem de resoldre una integral que no és immediata, haurem de descompondre-la en una o més integrals que sí són immediates i després resoldre cadascuna d’aquestes intergrals.
Els procediments de descompondre la integral original en integrals de la taula d’integrals immediates són els mètodes d’integració.
La tria del mètode d’integració dependrà de la funció que volem integrar. L’ordre de verificació del mètode d’integració més adient, és:
- Integral immediata (vist en l’apartat anterior)
- Integral quasi immediata
- Integral per parts
- Descomposició en fraccions simples
- Trigonomètrica
- De substitució
En aquesta entrada veurem com es fan sobretot els mètodes \(1,2,3,4\).
4.1 Integrals quasi immediates
Són integrals que no són immediates però que es poden transformar fàcilment en immediates fent algunes transformacions simples. Es resolen usant la taula d’integrals i les propietats de les integrals. De fet, es resolen per mètodes de susbstitució molt senzills.
Exemple:
\(\int \frac{x}{x²+6} \enspace dx \\
[u=x²+6, \, du=2x \; dx]\\
\frac{1}{2}\int \frac{2x}{x²+6} \enspace dx\\
\frac{1}{2}\int \frac{du}{u}\\
\frac{1}{2}\ln u+C\\
\frac{1}{2}\ln (x²+6)+C\\
\)
En aquest exemple, hem usat la tercera integral immediata de la taula d’integrals i la primera propietat de les integrals per a resoldre la integral de l’exemple.
4.3 Integrals per parts
Quan la funció que volem integrar és el producte de dues funcions i no es una integral immediata o quasi immediata, intentarem resoldre-la per parts.
La fórmula que usarem per a aplicar aquest mètode és \(\int {u \; dv}=u \cdot v – \int {v \; du}\). El perquè d’aquesta fórmula és:
\(d(u \cdot v)=v \cdot du + u \cdot dv\\
\int {d(u \cdot v)}=\int {v \cdot du} + \int{u \cdot dv}\\
\int {u \cdot dv}=u \cdot v-\int v \cdot du+C
\)
La integral \(\int v \; du\) ha de ser més fàcil de resoldre que la integral original \(\int u \; dv\) i el terme de susbstitució \(dv\) ha d’incloure sempre el terme \(dx\) de la integral original.
Exemple:
\(I=\int \ln x \; dx\\
u=\ln x \rightarrow du=\frac{dx}{x}\\
dv=dx \rightarrow v=\int {dx}=x\\[1cm]
I=\ln x \cdot x-\int{x \frac{dx}{x}}\\
I=\ln x \cdot x-\int{dx}\\
I=\ln x \cdot x-x\\
I=x(\ln x -1)+C\\
\)
De vegades, quan la integral està formada per les funcions \(e^u, \; \sin x/ \cos x\), haurem d’integrar per parts dues o més vegades:
\(I=\int {e^{x} \, \sin x \; dx} \\
u=\sin x \rightarrow du= \cos x \; dx\\
dv=e^x \; dx \rightarrow v=\int {e^x \; dx}=e^x\\[1cm]
\int {u \; dv}=\int { e^x \; \sin x \; dx}\\
u \cdot v= \sin x \cdot e^x\\
\int {v \; du}=\int e^x \; \cos x \; dx\\[1cm]
I=\sin x \; e^x-\int e^x \; \cos x \; dx\\
I=\sin x \; e^x- \; I_1\\[1cm]
I_1=\int e^x \; \cos x \; dx\\
u=\cos x \rightarrow du= -\sin x \; dx\\
dv=e^x \; dx \rightarrow v=\int {e^x \; dx}=e^x\\[1cm]
I_1= \cos x \; e^x+\int{\sin x \; e^x \; dx}\\
I_1=\cos x \; e^x+I\\
I=\sin x \; e^x-(\cos x \; e^x+I)\\
2I=\sin x \; e^x-\cos x \; e^x\\
I=\frac{e^x(\sin x-\cos x)}{2}
\)
2.4 Per descomposició en fraccions simples
La descomposició en fraccions simples és el procediment invers de l’operació de suma de fraccions algebraiques.
2.4.1 Si N(x) ≥ D(x):
Quan la funció que volem integrar és una funció racional \(f(x)=\frac{N(x)}{D(x)}\) i la integral no es pot resoldre més fàcilment per cap dels mètode anteriors, farem servir aquest mètode, tenint em compte que:
\(N(x)=q(x) \cdot D(x)+r(x)\\
\frac{N(x)}{D(x)}=q(x)+\frac{r(x)}{D(x)}\\
\)
\(N(x)\) és el polinomi del numerador, \(D(x)\) és el polinomi del denominador, \(q(x)\) és el polinomi del quocient i \(r(x)\) és el polinomi residu de la divisió polinòmica.
Per a resoldre la integral, farem el següents passos:
- Farem la divisió polinòmica \(\frac{N(x)}{D(x)}\).
- Descompondrem la funció f(x) en dues o més integrals: \(q(x)+\frac{r(x)}{D(x)}\).
- Resoldrem cada integral amb el mètode més adient.
Exemple:
\(\int {\frac{x³+2x²-5x+1}{x²+1}}\\[1cm]
1. \; \frac{x³+2x²-5x+1}{x²+1}=(x+2)-\frac{6x+1}{x²+1}\\
2. \; \int {x \; dx}+2 \int {dx}-6 \int{\frac{x}{x²+1} \; dx}-1 \int {\frac{dx}{x²+1}}\\
3. \; \int {x \; dx}+2 \int {dx}-\frac{6}{2} \int{\frac{2x}{x²+1} \; dx}-1 \int {\frac{dx}{x²+1}}\\
\frac{x²}{2}+2x-3 \ln {(x²+1)}-1 \arctan {(x²+1)}+C
\)
2.4.2 Si N(x) < D(x):
Com que no és possible fer la divisió polinòmica, farem la descomposició en fraccions parcials. Recordeu que la descomposició en fraccions parcials és el procediment invers de l’addició de fraccions.
La seqüència del procediment és la següent:
Exemple:
1.Factoritzarem el denominador de la funció racional fins a obtenir-ne polinomis irreductibles. Els factors seran, o bé binomis lineals (x+a), o bé polinomis quadràtics irreductibles (ax²+bx+c).
2.Transformarem la funció racional en diferents fraccions de la següent manera: la fracció que correspon a cada factor lineal (x+a) és \(\ \frac{A}{(x+a)}\) (A és un valor constant).
La fracció que correspon a cada factor quadràtic (ax²+bx+c) és \(\frac{Ax+B}{(ax²+bx+c)}\). En ambdós casos, a cada factor li corresponen tantes fraccions com multiplicitat o nombre de solucions múltiples tingui el factor.
Exemple:
\(
1.\frac{2x²+5}{x⁷+6x⁶+14x⁵+20x⁴+25x³+22x²+12x+8}\\
\frac{2x²+5}{(x+2)³ (x²+1)²}\\[0.5cm]
\text{Factor lineal: (x+2), multiplicitat 3}\\
\text{Factor quadràtic: (x²+1), multiplicitat 2}\\[0.5cm]
2.\frac{2x²+5}{(x+2)³ (x²+1)²}=\frac{A}{(x+2)³}+\frac{B}{(x+2)² }+\frac{C}{(x+2)¹}+\frac{Dx+E}{(x²+1)²}+\frac{Fx+G}{(x²+1)¹}
\)]
3.Farem l’addició de fraccions i eliminarem els denominadors.
4.Igualarem els coeficients de cada monomi del numerador amb els coeficients dels monomis semblants del denominador.
5.Resoldrem el sistema d’equacions obtingut.
6.Un cop feta la descomposició de la funció racional en fraccions més simples, farem les integrals de cada fracció.
Exemple:
\(\int {\frac{4x²-2x}{x⁴ +4x³+5x²+4x+4} \; dx}\\[1cm]
1.\\
\frac{4x²-2x}{x⁴ +4x³+5x²+4x+
4}=\frac{4x²-2x}{(x+2)² \cdot (x²+1)}\\[0.5cm]
2. \\
\frac{4x²-2x}{x⁴+4x³+5x²+4x+4}=\frac{A}{(x+2)²}+\frac{B}{(x+2)}+\frac{Cx+D}{(x²+1)}\\[0.5cm]
3.\\
4x²-2x=A(x²+1)+B(x+2)(x²+1)+(Cx+D)(x+2)²\\
A(x²+1)+B(x³+2x²+x+2)+(Cx+D)(x²+4x+4)\\
Ax²+A+Bx³+2Bx²+Bx+2B+Cx³+4Cx²+4Cx+Dx²+4Dx+4D\\[0.5cm]
4.\\
0x³=(B+C)x³\\
4x²=(A+2B+4C+D)x²\\
-2x=(B+4C+4D)x\\
0=A+2B+4D\\[0.5cm]
5.\\
0=B+C\\
4=(A+2B+4C+D)\\
-2=(B+4C+4D)\\
0=A+2B+4D\\
A=4,B=-\frac{4}{10},C=\frac{4}{10}, \, D=-\frac{8}{10}\\[0.5cm]
6.\\
\int {\frac{4x²-2x}{x⁴ +4x³+5x²+4x+
4}}= 4\int{\frac{dx}
{(x+2)²}}-\frac{4}{10}\int{\frac{dx}{(x+2)}}+\int { \frac{\frac{4x}{10}-\frac{8}{10}}{(x^2+1)} }\\
-\frac{4}{x+2}-\frac{4}{10}\ln(x+2)+\frac{1}{10}[ \int{ \frac{4x}{x²+1} \; dx-8\int{\frac{dx}{x²+1}} } \; dx ]\\
-\frac{4}{x+2}-\frac{4}{10}\ln(x+2)+\frac{1}{10}[2 \; \ln {(x²+1)}-8 \arctan{(x²+1)} ]+C
\)
2.5 Per substitució o canvi de variable
En aquest mètode es modifica la funció \(f(x)\) substituint-ne una part per una expressió algebraica perquè la funció resultant sigui més fàcil d’integrar. Aquests expressió es funció d’una nova variable independent \(g(t)\).
El mètode de substitució o de canvi de variable per a calcular primitives té el seu origen en la regla de la cadena per a derivades.
El procediment per a aquest mètode és:
1.Trobar el canvi de variable adient que transformi la funció \(f(x)\) en una altra de més senzilla.
2.Calculem la funció \(g(t)\) que resulta de fer el canvi de variable i substituim \(f(x)\) per aquesta funció.
3.Fent servir el canvi de variable, calculem i substituim \(dx\).
4.Resolem la integral \(\int {g(t) \; dt}\).
5.Desfem el canvi.
Exemple:
\(\int {\frac{x²}{\sqrt{1+x³}}dx}\\[1cm]
1.\\
1+x³=t²\\[0.5cm]
2.\\
x² \hspace{1.3cm}: \; x=\sqrt[3]{t²-1} \Rightarrow x²=\sqrt[3]{(t²-1)²}\\[0.5cm]
\sqrt{1+x³}: \;\sqrt{1+x³}=t²\\[0.5cm]
3.\\d(1+x³)=d(t²), \; 3x²dx=2tdt\\[0.5cm]
4.\\
\frac{1}{3}\int {\frac{2t}{t}dt}\\
\frac{2}{3}t+C\\
5.\\
\frac{2}{3}\sqrt{1+x³}+C
\)
2.5.1 Canvis de variable més habituals
| \( \int f(ax+b) \ dx = \frac {1}{a} \int f(u) \ du\) | \(u=ax+b\) |
| \( \int f(\sqrt{ax+b} \ dx = \frac{2}{a} \int u\cdot f(u) \ du\) | \(u=\sqrt{=ax+b}\) |
| \( \int f(\sqrt[n]{ax+b}) \ dx= \frac{n}{a} \int u^{n-1} f(u) \ du\) | \(u=\sqrt[n]{ax+b}\) |
| \( \int f(\sqrt{a^2+b^2}) \ dx= a \int f(a\cdot \cos u ) \ du\) | \(u=a\cdot\sin u\) |
| \( \int f(e^{ax}) \ dx = \frac{1}{a} \int \frac{f(u)}{u} \ du\) | \(u=e^{ax}\) |
| \( \int f(\ln x) \ dx=\int f(u) e^u du\) | \(u=\ln x\) |
3. Integrals definides
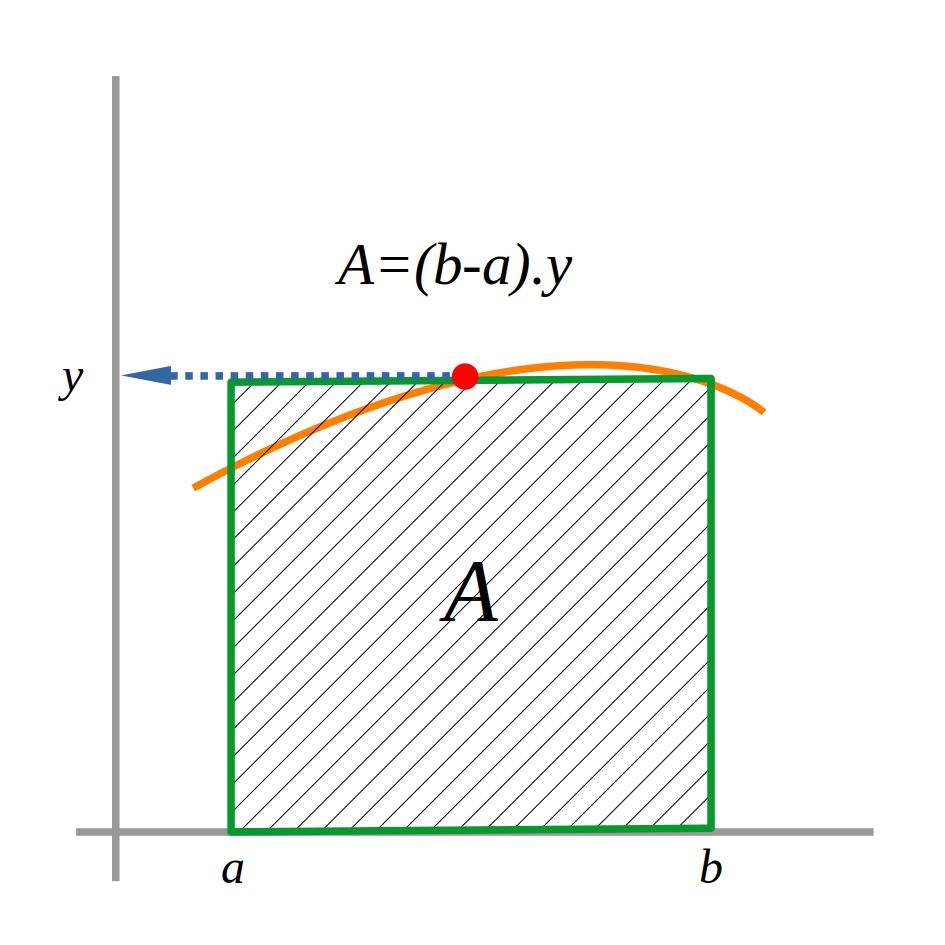
Una integral definida és la integració d’una funció \(f(x)\) en un interval del seu domini: \(A=\int_{a}^{b}{f(x)\; dx}\).
\(a,b\) són els límits inferior i superior de l’interval.
El valor \(A\) de la integral representa l’àrea tancada per la funció entre els límits \(a,b\) i l’eix \(OX\).
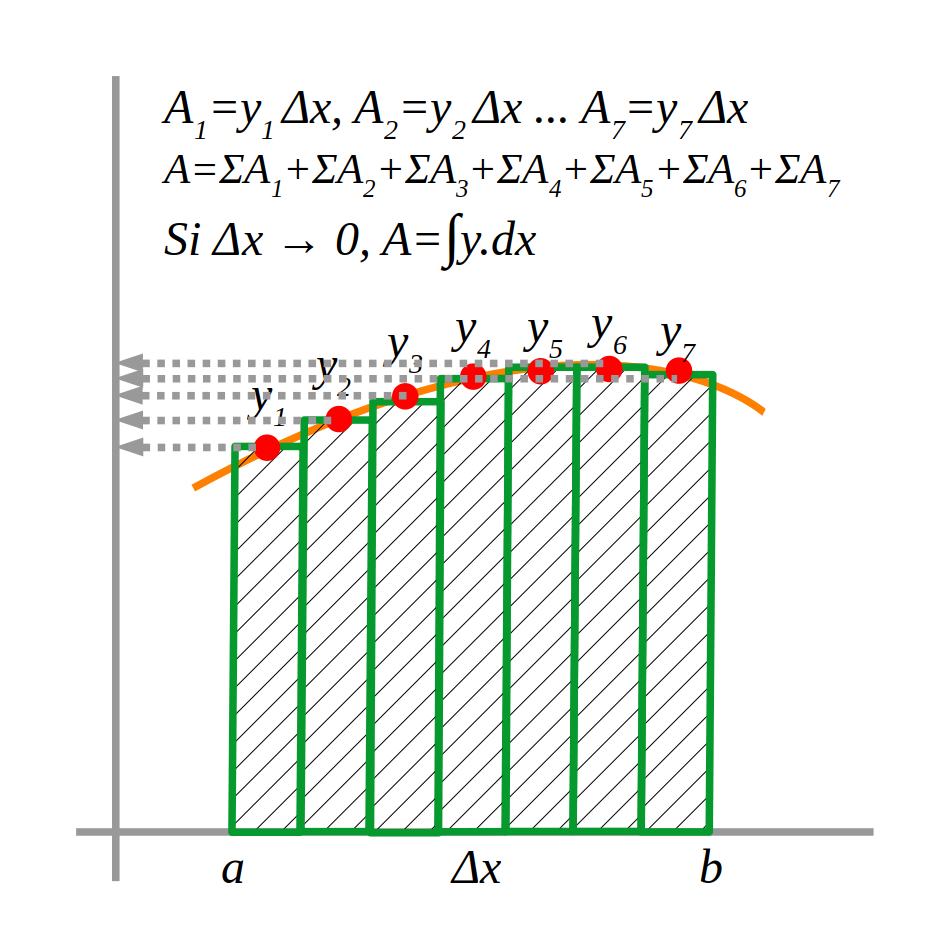
Si calculem l’àrea que hi ha dessota de la funció (línia carabassa) aproximant-la a la del rectangle verd, podríem fer un error important. Però si dividim l’àrea en rectangles petits, calculem l’àrea de cadascun, i en fem la suma, el resultat serà més aproximat i l’error més petit. El cálcul serà més precís com més estrets siguin els rectangles. Si l’amplada dels rectangles és infinitesimal (infinitament petita), el resultat serà pràcticament exacte ( \(dx=\Delta x \rightarrow 0\)).
3.1 Regla de Barrow
Per fer el cálcul d’una intergral definida usem la regla de Barrow (el segon teorema fonamental del càlcul:
\(A=\int_{a}^{b}{f(x) \; dx}=F(b)-F(a)\)Exemple:
\(\int_{2}^{4}{x^2-3x+6} \; dx\\
{\frac{x³}{3}-3\frac{x²}{2}+6x}\; |^{4}_{2}\\
\frac{1}{3}(4³-2³)-\frac{3}{2}(4²-2²)+6(4-2)\\
\frac{1}{3}(64-8)-\frac{3}{2}(16-4)+6(4-2)\\
\frac{56}{3}-\frac{3}{2}(12)+6(2)\\
\frac{56}{3}-\frac{36}{2}+12=\frac{38}{3}u^2
\)
El procediment per a calcular l’àrea tancada per dues o meś funcions entre els límits \(a, b\) i l’eix \(OX\), és el següent:
- Calculem els límits inferior i superior resolent el sistema d’equacions format per les equacions de les funcions.
- Calculem l’àrea tancada per les funcions entre límits i l’eix OX: \(A=|\int_{a}^{b}{(y_1-y_2)}|\)
El càlcul de la integral es fa amb valor absolut per evitar que l’àrea sigui negativa.
Exemple:
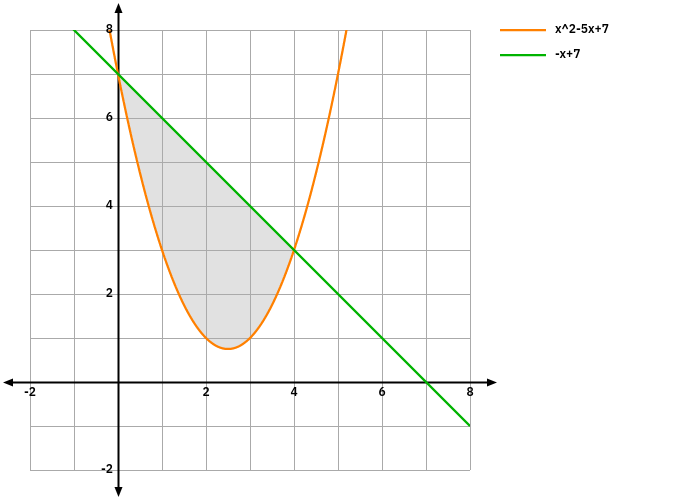
y_1=x²-5x+7\\
y_2=-x+7\\[1cm]
1.\\
y_1=y_2\\
x²-5x+7=-x+7\\
x²-4x=0\\
x=0,+4\\[1cm]
2.\\
A=|\int_{0}^{+4}{(x²-4x) \; dx}\; |\\
|{\frac{x³}{3}–4\frac{x²}{2}|}^{+4}_{0}|\\
|\frac{1}{3}[{4³}-(0)³]–2[(4²-(0)²]|\\
|\frac{64}{3}-32|=\frac{32}{3}u²
\)

 RSS CEEdukat
RSS CEEdukat