Còniques

1. Definició

Les còniques són les corbes del pla que s’obtenen quan es talla una superfície cònica amb un pla.

L’equació general d’una cònica amb els eixos paral·lels als eixos de coordenades és:

\[Ax²+By²+Cx+Dy+E=0\]

Si \[A=B\], és una circumferència (\[x²+y²+Ax+By+C=0\]).

Si \[A \neq B\] i són del mateix signe, és una el·lipse (\[Ax²+By²+Cx+Dy+E=0\]).

Si \[A \neq B\] i són de signe diferent, és una hipèrbola

\[
Ax²-By²+Cx+Dy+E=0\\
-Ax²+By+Cx+Dy+E=0
\]

Si \[A\] o \[B\] són zero, és una paràbola

\[
Ax²+Bx+Cy+D=0\\
Ay²+Bx+Cy+D=0
\]

Si \[A\] i \[B\] són zero, és una recta (\[Cx+Dy+E=0\]).

Per a calcular la intersecció d’una cònica amb els eixos o amb altres funcions es farà el sistema d’equacions que en resulta.

2. Circumferència

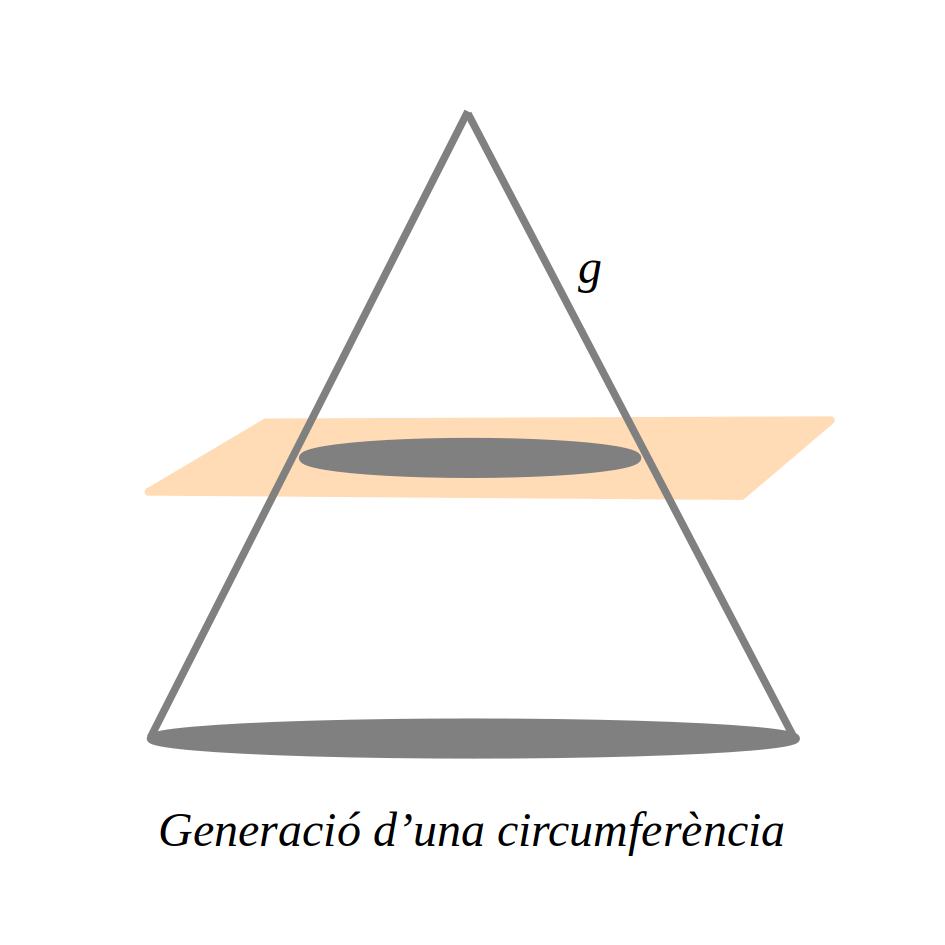
Una circumferència és el conjunt de tots els punts d’un pla la distància dels quals al centre és constant.

\[(x-a)²+(y-b)²=r²\]

Es genera quan una superfície cònica és tallada per un pla horitzontal paral·lel a la base de la superfície cònica.

2.1 Elements de la circumferència:

Els elements d’una circumferència són el centre i el radi.

Podem dibuixar una circumferència amb un centre i un radi o bé amb tres punts.

2.2 Equació general:

\[x²+y²+Ax+By+C=0\]

Per a calcular \[A,B,C\] a partir de l ‘equació reduïda:

\[(x-a)²+(y-b)²=r²\\
(x²-2xa+a²)+(y²-2yb+b²)=r²\\
x^2+y²-2xa-2yb+a²+b²=r^2\\
x²+y²+Ax+By+C=0\\
A=-2a, \; B=-2b, \; C=a²+b²-r²
\]

Per tal que la circumferència existeixi a \[\mathbb{R}\] s’ha de complir que \[(\frac{A}{2})²+(\frac{B²}{2})²-C>0\].

Exemple:

\[
(x-3)²+(y-2)²=9\\
a=3, \; A=-6\\
b=2, \; B=-4\\
C=(-3)²+(2)²-(3)²=4\\
x²+y²-6x-4y+4=0
\]

2.3 Equació reduïda:

\[
C(0,0): x²+y²=r²\\
[C(a,b): (x-a)²+(y-b)²=r²
\]

Per a calcular l’equació reduïda a partir de la general, fem:

1. Si els coeficients iguals de la \[x\] i la \[y\] són diferents d’\[1\], els reduïm a \[1\] dividint tota l’equació pel valor dels coeficients.
2. Calculem \[A,B\] i \[r\] .
3. Escrivim l’equació reduïda i dibuixem la circumferència.

\[
4x²+4y²-24x-16y+16=0\\[1cm]
1.\\
x²+y²-6x-4y+4=0\\[0.5cm]
2.\\
a=-\frac{A}{2}=-\frac{-6}{2}=3\\
b=-\frac{B}{2}=-\frac{-4}{2}=2\\
C=a²+b²-r²\\
4=3²+2²-r²=9\\
-r²=4-9+4\\
r=3\\[0.5cm]
3.\\
(x-3)²+(y-2)²=9
\]

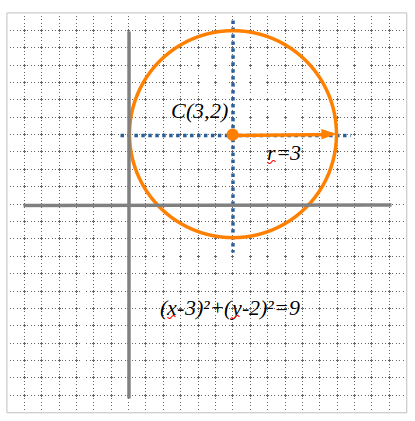
2.4 Potència d’una circumferència

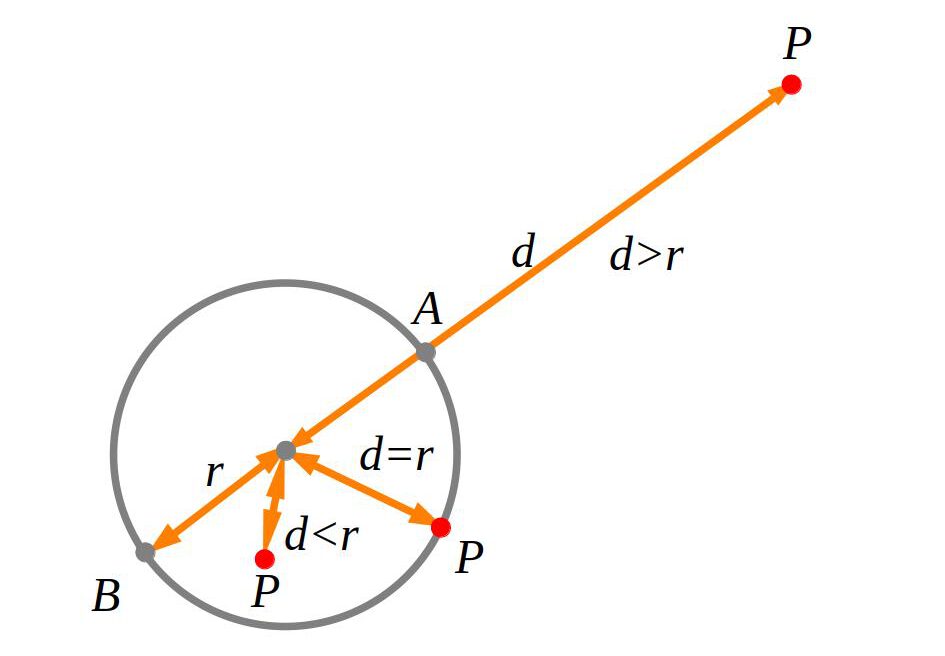
La potència d’un punt P respecte a una circumferència és: \[\overline{PA} \cdot \overline{PB}=d²-r²\]. El punt pot ser exterior, interior o de la circumferència.

Si ens donen un punt i l’equació d’una circumferència, per a calcular al distància d haurem de trobar l’equació de la recta i els punts d’intersecció amb la circumferència fent un sistema d’equacions no lineals. També haurem de recordar els coneixements de vectors en el pla per a calcular les distàncies.

El procediment que hem de seguir és:

1. Trobem el centre i el radi de la circumferència i determinem si el punt és exterior, interior o de la circumferència.
2. Calculem l’equació de la recta que passa pel punt P i el punt del centre de la circumferència.
3. Trobem els punts d’intersecció de la circumferència i la recta.
4. Calculem la distància d i la potència de P a la circumferència.

\[
1.\\
x²+y²+6x-6y+9=0\\
a=-\frac{A}{2}=-\frac{6}{2}=-3\\
b=-\frac{-6}{2}=-\frac{6}{2}=+3\\
r²=a²+b²-C=(-3)²+(+3)²-9=9, \;r=3\\
C(a,b)=(-3,+3)\\
r=3\\
(x+3)²+(y-3)²=9\\
(+3)²+(+1)²+6 \cdot 3-6 \cdot 1+9=31 \; \text{[31>9, (3,1)és un punt exterior]}
\\[1cm]
2.\\
\vec v_r=(3,1)-(-3,3)=(6,-2)\\
\vec v_{r\perp}=(2,6)\\
r:2x+6y+C=0, P(3,1) \Rightarrow D=-12\\
r:2x+6y-12=0
\\[1cm]
3.\\
\begin{cases}
2x+6y-12=0\\
(x+3)²+(y-3)²=9
\end{cases}\\
(A):x_1= -3+\frac{9}{\sqrt{10}} , \; y_1= +3-\frac{3}{\sqrt{10}} \\
(B):x_2= -3-\frac{9}{\sqrt{10}} , \; y_2= +3+\frac{3}{\sqrt{10}}
\\[1cm]
4.\\
\left| \overline{PA} \right|=\left| (-3+\frac{9}{\sqrt{10}},+3-\frac{3}{\sqrt{10}})-(3,1) \right|=\left| (-6+\frac{9}{\sqrt{10}},+2-\frac{3}{\sqrt{10}}) \right|=3.32 \; u.\\
Potència=d²-r²=(3.32)²-(3)²=2.05 \; u².
\]

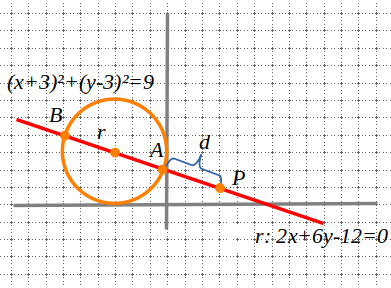
2.5 Eix radical

L’eix radical de dues circumferències és el lloc geomètric dels punts que tenen la mateixa potència respecte a cada circumferència. És una recta perpendicular a la recta que uneix el centres de cada circumferència.

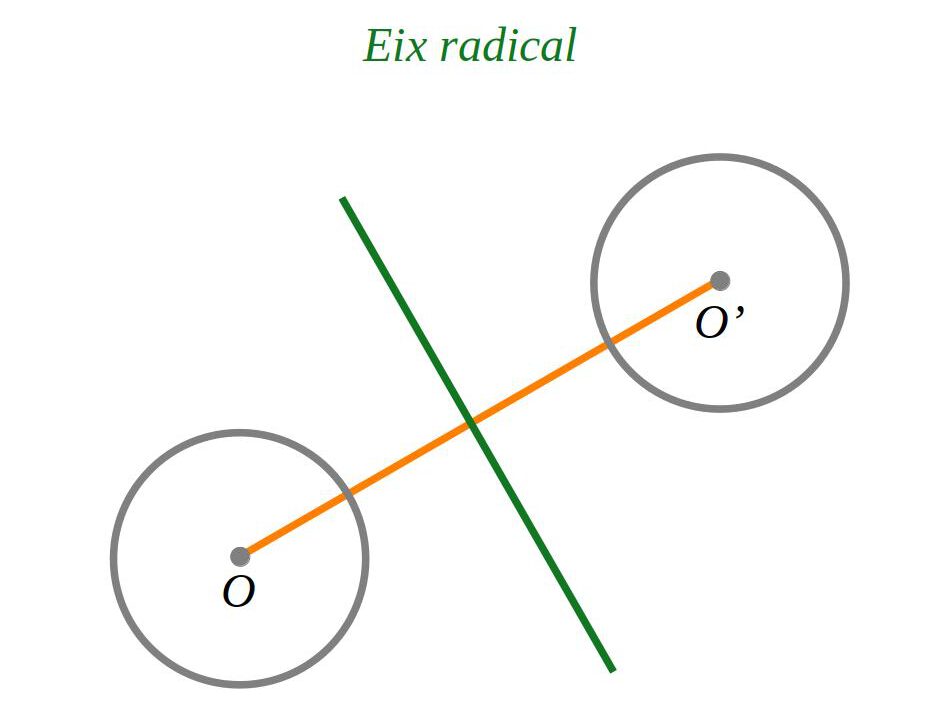
L’equació de l’eix radical és:

\[
x² + y^2 +Ax +By +C=0
\\
x² + y^2 +A’x +B’y +C’=0
\\[0.5cm]
x² + y^2 +Ax +By +C=x² + y^2 +A’x +B’y +C’=0
\\
(A-A’)x + (B-B’)y+(C-C’)=0
\]

3. El·lipse

És el lloc geomètric del punts del pla que la suma de les distàncies a dos punts fixos (focus) és constant.

Si \[\overline{PF},\overline{PF’}\] són el radis vectors:

\[
\overline{PF}+\overline{PF’}=2a
\]

Una el·lipse es genera quan una superfície cònica és tallada per un pla que no és paral·lel a la generatriu de la superfície cònica.

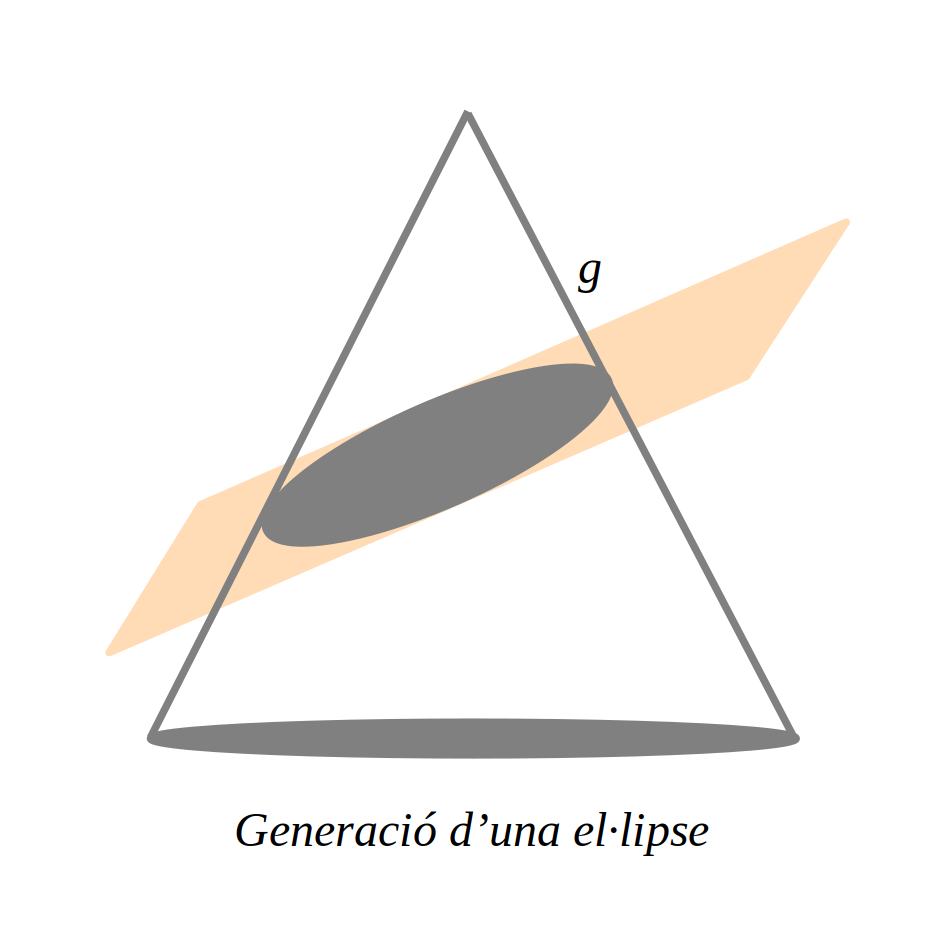
3.1 Elements de l’el·lipse

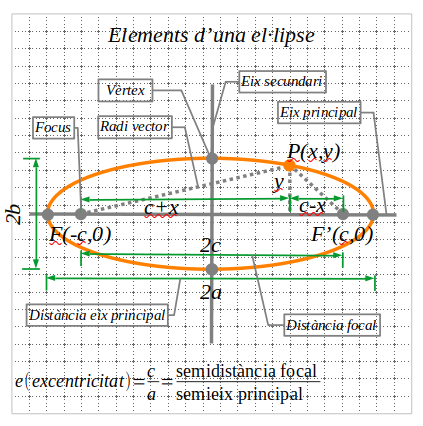
Per a calcular els radis vectors fem:

\[\overline{PF}=a-ex, \; \overline{PF’}=a+ex\]

Per a calcular l’eix secundari fem:

\[b=\sqrt{a²-c²}\]

Per a calcular els vèrtexs d’una el·lipse centrada al \[(0,0)\] fem la intersecció de l’equació de l’el·lipse amb els eixos \[(x=0,\; y=0)\].

3.2 Equació general

\[Ax²+By²+Cx+Dy+E=0\]

3.3 Equació reduïda

Per a obtenir l’equació reduïda a partir de la general i extreure’n els elements de l’el·lipse, fem:

1. Agrupem el termes amb \[x\] i el termes amb \[y\].
2. Fem el factor comú de cada agrupació.
3. Obtenim els quadrats perfectes de cada agrupació.
4. Calculem l’equació reduïda i la simplifiquem.
5. N’extraiem els elements.

\[
4x²+9y²-8x+18y-23=0
\\[1cm]
1.\\
(4x²-8x)+(9y²+18y)-23=0
\\[1cm]
2.\\
4(x²-2x)+9(y²+2y)-23=0
\\[1cm]
3\\
x²-2x=(x-1)²-1\\
y²+2y=(y+1)²-1
\\[1cm]
4.\\
4[(x-1)²-1]+9[(y+1)²-1]-23=0\\
4[(x-1)²]+9[(y+1)²]-23-4-9=0\\
4[(x-1)²]+9[(y+1)²]=36\\
\frac{4[(x-1)²]}{36}+\frac{9[(y+1)²]}{36}=\frac{36}{36}\\
\frac{(x-1)²}{9}+\frac{(y+1)²}{4}=1
\\[1cm]
5.\\
C(1,-1)
\\[0.5cm]
c²=a^2-b²=3²-2²=5\\
c=\sqrt{5}\\
F'(1+\sqrt{5},-1), \; F(1-\sqrt{5},-1)
\\[0.5cm]
V_x(1 \pm 3,-1) \Rightarrow (4,-1), \; (-2,-1)\\
V_y(1,-1 \pm 2) \Rightarrow (1,1), \; (1,-3)\\
\]

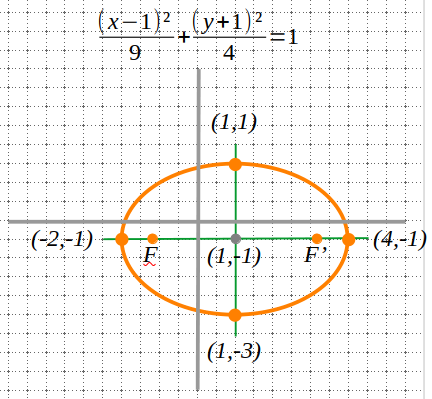
Segons la posició i el centre de l’el·lipse, els focus, els vèrtexs i l’equació reduïda seran:

3.3.1 Horitzontal

3.3.1.1 C(0,0)

\[
F(-c,0),\; F'(+c,0)\\
V_x(\pm a,0), \; V_y(0,\pm b)\\
\frac{x²}{a²}+\frac{y²}{b²}=1\]

3.3.1.2 C(x0, y0)

\[
F(x_0-c,y_0),\; F'(x_0+c,y_0)\\
V_x(x_o \pm a,0), \; V_y(x_0,y_o\pm b)\\
\frac{(x-x_0)²}{a²}+\frac{(y-y_0)²}{b²}=1
\]

3.3.2 Vertical

3.3.2.1 C(0,0)

\[
F(0,-c),F'(0,+c)\\
V_x(\pm b,0), \; V_y(x_0,\pm a)\\
\frac{x²}{b²}+\frac{y²}{a²}=1
\]

3.3.2.2 C(x0, y0)

\[
F'(x_0,y_0-c),F(x_0,y_0+c)\\
V_x(x_0\pm b,y_0), \; V_y(x_0,y_0 \pm a)\\
\frac{ (x-x_0)²}{b²}+\frac{(y-y_0)²}{a²}=1
\]

4. Hipèrbola

És el lloc geomètric dels punts del pla que fan que la diferència de les distàncies a dos punts fixos (focus) sigui constant \[2a\].

\[\overline{PF}-\overline{PF’}=2a\]

S’obté una hipèrbola quan un pla talla verticalment dues superfícies còniques oposades pel vèrtex:

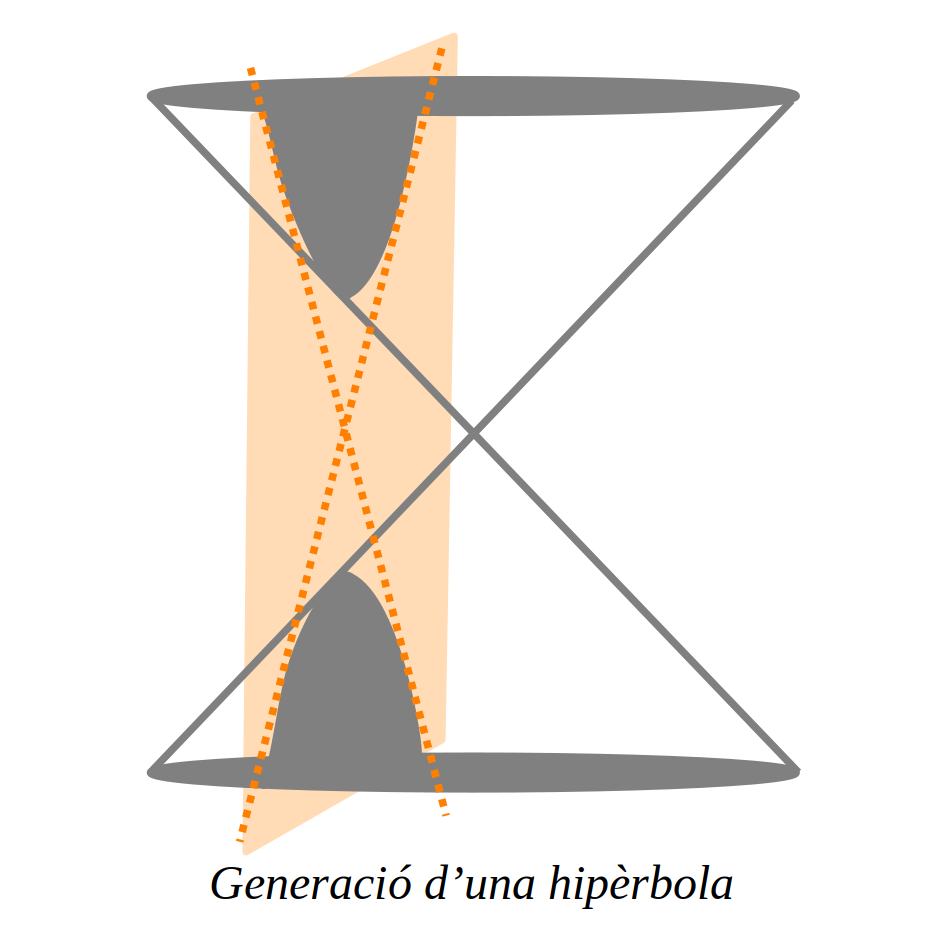
4.1 Elements d’una hipèrbola

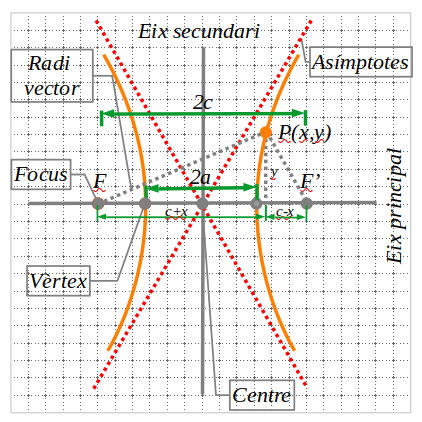
A l’eix principal l’anomenem eix real i a l’eix secundari eix imaginari.

Per a calcular els radis vectors d’una hipèrbola, fem:

\[\overline{PF}=\left|ex-a\right|, \; \overline{PF’}=\left|ex-a\right|\]

Els vèrtexs d’una hipèrbola amb \[C(0,0)\] es calculen fent la intersecció del eixos amb la hipèrbola \[x=0, \; y=0\].

Les asímptotes es calculen fent:

\[y=\pm \frac{b}{a}x\]

4.2 Equació general

\[
Ax²-By²+Cx+Dy+E=0\\
-Ax²+By²+Cx+Dy+E=0
\]

4.3 Equació reduïda

Per a calcular l’equació reduïda d’una hipèrbola a partir de la general, fem:

1. Agrupem el termes amb \[x\] i el termes amb \[y\].
2. Fem el factor comú de cada agrupació.
3. Obtenim els quadrats perfectes de cada agrupació.
4. Calculem l’equació reduïda i la simplifiquem.
5. N’extraiem els elements.

\[
4x²-9y²-8x+36y+4=0\\[1cm]
1.\\
(4x²-8x)-(9y²-36y)+4=0\\
2.\\
4(x²-2x)-9(y²-4y)+4=0\\
3.\\
x²-2x=(x-1)²-1\\
y²-4y=(y-2)²-4\\
4.\\
4(x-1)²-9(y-2)²=-36\\
\frac{4(x-1)²}{-36}-\frac{9(y-2)²}{-36}=1\\
\frac{(x-1)²}{-9}-\frac{(y-2)²}{-4}=1\\
\frac{(y-2)²}{4}-\frac{(x-1)²}{9}=1\\[1cm]
5.\\
C(1,2)\\
a=2, \;b=3, \; c=\sqrt{a²+b²}=\sqrt{13}\\
V(1,2\pm 2)=(1,0), \;(1,4)\\
F(1,2+\sqrt{13}), \; F'(1,2-\sqrt{13})\\
(y-2)²=\frac{4}{9}(x-1)² \Rightarrow y=\pm \frac{2}{3}(x-1)+2\\
y=\frac{2}{3}x+\frac{4}{3}\\
y=-\frac{2}{3}x+\frac{8}{3}
\]

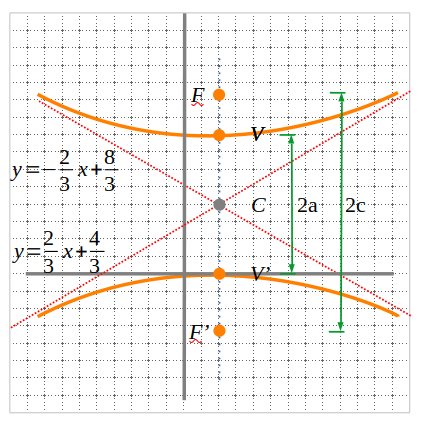
Segons la posició i el centre de la hipèrbola, els focus, els vèrtexs i l’equació reduïda seran:

4.3.1 Horitzontal

4.3.1.1 C(0,0)

\[
C(0,0)\\
F(x_0-c,y_0),F'(x_0+c,y_0)\\
V_x(x_0\pm a,y_0)\\
\frac{(x-x_0)²}{a²}+\frac{(y-y_0)²}{b²}=1
\]

4.3.1.2 C(x0,y0)

\[
C(x_0,y_0)\\
F(x_0-c,y_0),F'(x_0+c,y_0)\\
Vx(x_0 \pm a, y_0)\\
\frac{(x-x_0)²}{a²}+\frac{(y-y_0)²}{b²}=1
\]

4.3.2 Vertical

4.3.2.1 C(0,0)

\[
C(0,0)\\
F(0,-c),F'(0,+c)\\
V_y(0,\pm a)\\
\frac{(x-x_0)²}{b²}+\frac{(y-y_0)²}{a²}=1
\]

4.3.2.2 C(x0,y0)

\[
C(x_0,y_0)\\
F(x_0,y_0-c),F'(x_0,y_0+c)\\
V_y(x_0,y_0 \pm a)\\
\frac{(x-x_0)²}{b²}+\frac{(y-y_0)²}{a²}=1
\]

5. Paràbola

Una paràbola és el lloc geomètric dels punts del pla que equidisten del focus i de la directriu:

\[y²=2px\] \[
d(F,P)=\sqrt{(x-\frac{p}{2})²+y²}\\
d(P,d)=\left|x+\frac{p}{2}\right|\\
\sqrt{(x-\frac{p}{2})²+y²}=\left|x+\frac{p}{2}\right|\\
y²=2px
\]

Una paràbola s’obté tallant de forma obliqua una superfície cònica.

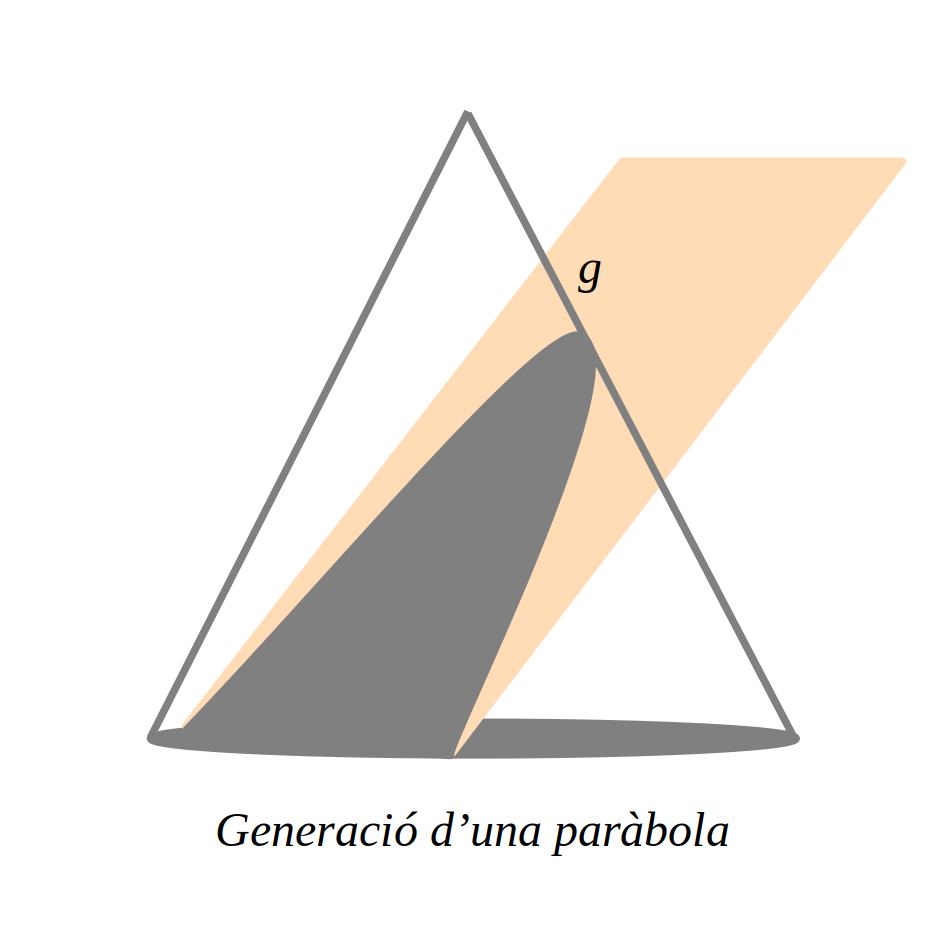
5.1 Elements de la paràbola

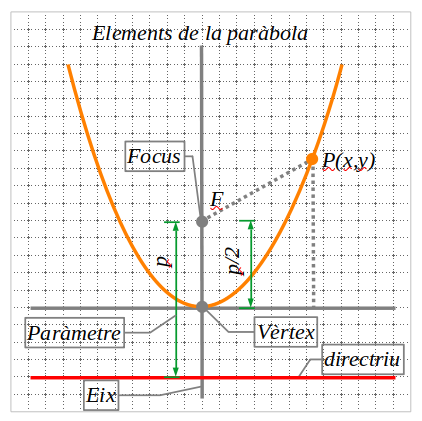
La distància del focus a la directriu s’anomena paràmetre.

L’eix és la recta que passa pel focus i és perpendicular a la directriu.

El vèrtex és el punt d’intersecció de la paràbola amb l’eix.

5.2 Equació general

\[
Ax²+Bx+Cy+D=0\\
Ay²+Bx+Cy+D=0
\]

1. Separarem els termes amb \[x\] dels termes amb \[y\] i dividirem tota l’equació pel coeficient del terme quadrat.
2. Farem el quadrat perfecte del terme quadrat i susbstituirem l’expressió calculada a l’equació anterior.
3. Calcularem l’equació de la paràbola transformant l’expressió del punt anterior en una la forma \[(y-y_0)²=\pm 2p(x-x_0)\], o bé de la forma \[(x-x_0)²=\pm 2p(y-y_0)\] extraent el factor comú del coeficient \[ x\] o \[y\] de primer grau de la dreta de la igualtat.
   
   Si l’equació té un terme \[y²\], la transformarem en una de la primera forma. Si té un terme \[x²\], la transformarem en una equació de la segona forma.
4. Definirem els elements de la paràbola i en calcularem un parell de punts per a poder dibuixar-la.

\[
2x²+8x+3y-5=0
\\[1cm]
1.\\
2x²+8x=-3y+5\\
x²+4x=-\frac{3}{2}+\frac{5}{2}
\\[1cm]
2. \\
x²+4x=(x+2)²-4
\\[1cm]
3.\\
(x+2)²-4=-\frac{3}{2}y+\frac{5}{2}\\
(x+2)²=-\frac{3}{2}y+\frac{13}{2}\\
(x+2)²=-\frac{3}{2}(y-\frac{13}{3}) \enspace [(x-x_o)²=\pm 2p(y-y_0)]
\\[1cm]
4.\\
x_0=-2, \; y_0=\frac{13}{3}\\
-2p=-\frac{3}{2} \Rightarrow p=\frac{3}{4}\\
V(-2,\frac{13}{3})\\
F(-2,\frac{13}{3}-\frac{3}{8})=(-2,\frac{95}{24})\\
y=\frac{13}{3}+\frac{3}{8}=\frac{113}{24} \text{ (directriu)}\\
(x+2)=\pm \sqrt{\frac{39}{6}} \; \text{( y=0)}\\
x=0.55, \; -4.56
\]

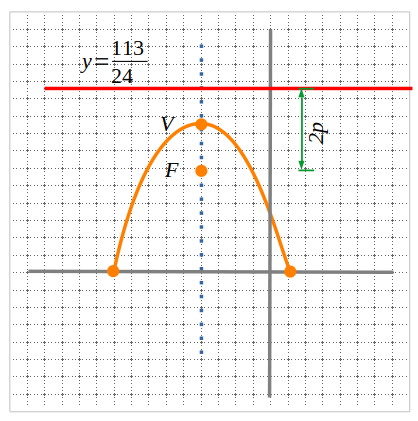
5.3 Equació reduïda

Segons si la paràbola té el vèrtex a \[V(0,0)\] i si la posició és vertical o horitzontal, la posició del focus, del vèrtex i l’equació reduïda serà:

5.3.1 Horitzontal V(0,0)

5.3.1.1 Focus a la dreta:

\[
F(\frac{p}{2},0)\\
y²=+2px
\]

5.3.1.2 Focus a l’esquerra

\[
F(-\frac{p}{2},0)\\
y²=-2px
\]

5.3.2 Vertical V(0,0)

5.3.2.1 Focus per sobre de l’eix

\[
F(0,\frac{p}{2})\\
x²=+2px
\]

5.3.2.2 Focus per sota de l’eix

\[
F(0,-\frac{p}{2})\\
x²=-2px
\]

5.3.3 Horitzontal (x0,y0)

5.3.3.1 Focus a la dreta

\[
F(x_0+\frac{p}{2},0)\\
(y-y_0)²=+2p(x-x_0)
\]

5.3.3.2 Focus a l’esquerra

\[
F(x_0-\frac{p}{2},0)\\
(y-y_0)²=-2p(x-x_0)
\]

5.3.4 Vertical (x0,y0)

5.3.4.1 Focus per sobre de l’eix:

\[
F(x_0,y_0+\frac{p}{2})\\
(x-x_0)²=+2p(y-y_0)
\]

5.3.4.2 Focus per sota de l’eix:

\[
F(x_0,y_0-\frac{p}{2})\\
(x-x_0)²=-2p(y-y_0)
\]