Instruccions abans de començar
1. Introducció
El 1884 el químic suec Arrhenius afirma en la teoria de dissociació iònica que, en dissolució aquosa, algunes substàncies es dissocien en ions positius i ions negatius que les fa conductores de l’electricitat.
Segons Arrhenius, un àcid és una substància que en dissolució aquosa es dissocia formant ions hidrogen (\[H^+\]) i una base es dissocia formant ions hidroxil (\[OH^-\]).
AH + H_2 O ⇌ A^- + H^+
\\
BOH + H_2 O ⇌ B^+ + OH^-
\]
Però hi ha substàncies que es comporten com a àcids o com a bases en dissolvents que no són aigua o que no es dissocien en aquests ions.
El 1923, Brönsted i Lowry ampliaren de forma independent la definició d’àcid i base d’Arrhenius dient que, un àcid és una espècie química que pot proporcionar ions \[H_ 3 O^+\] i una base en pot acceptar.
Quan un àcid perd un protó es forma la base conjugada, i quan una base en rep un és forma l’àcid conjugat de la base:
\[HA \text{(Àcid)} ⇌ A^- \text{(Base conjuagada)} + H^+
\\
BOH \text {(Base)} ⇌ B^+ \text { (Àcid conjugat)} + OH^-
\]
Més tard, Lewis amplia encara més la definició i diu que un àcid és una substància que pot acceptar un parell d’electrons i una substància bàsica proporciona un parell d’electrons.
Tanmateix, les substàncies sols mostraran el caràcter àcid o bàsic quan reaccionin amb altres substàncies que puguin rebre o donar protons. Hi ha substàncies, com l’aigua, que de vegades tenen caràcter àcid o bàsic segons la substància amb la qual reaccioni.
2. Equilibri iònic de l’aigua
La reacció d’ionització de l’aigua és una reacció en la qual una molècula d’aigua perd un protó i esdevé un ió hidroxil \[(OH^-)\]. El nucli d’hidrogen (\[H^+\]) agafa immediatament una molècula d’aigua per a formar un ió oxoni (\[H_3 O^+\]):
tot i que Arrhenius va proposar inicialment la reacció d’ionització
\[H_2 O ⇌ H⁺ + OH^-\]A causa de l’autoionització, l’aigua té una conductivitat elèctrica de 0.055 μS/cm.
La constant d’equilibri d’aquesta reacció és:
\[\displaystyle K_e=\frac{[ H_3 O^+] \cdot [OH^-]} {[H_2 O]^2}\]A 25 ºC les concentracions d’ions hidroni i hidroxil són iguals:
\[[H_3 O^+]=[OH^-]=1×10^{-7}\]I si calculem \[H_2 O\] a partir de la densitat de l’aigua a 25ºC:
\[\displaystyle [H_2 O]=0,997 \frac{g}{mL} \cdot {\frac{ 1 mol} {18g}} \cdot { \frac{1000 mL}{1L} }~=55,3 M\]Com que hi ha molt poques molècules dissociades, aproximadament 2 ppb, la reacció d’autoionització està desplaçada molt cap a l’esquerra i, per tant, la concentració d’aigua pràcticament no varia:
\[\displaystyle K_e \cdot [H_2 O]^2={[ H_3 O^+] \cdot [OH^-]} \rightarrow K_w={[ H_3 O^+] \cdot [OH^-]}=10^{-14}\]3. Grau d’acidesa (pH o potencial d’hidrogen)
L’acidesa és la capacitat d’una substància de proporcionar protons en solució aquosa.
L’escala de pH es defineix usant un elèctrode d’hidrogen o de vidre en contacte amb la solució estudiada i un altre elèctrode de referència (de calomelans, per exemple). Un elèctrode de referència té un potencial de reducció estable i conegut. L’estabilitat del potencial de l’elèctrode s’aconsegueix mitjançant un sistema redox amb concentracions tampó.
El pH és una escala que varia logarítmicament de 0 (molt àcid) a 14 (molt poc àcid) en dissolucions aquoses:
\[pH=-log [H_3 O^+]\]El pH de l’aigua pura és 7, però varia quan hi afegim un àcid o una base. Per la constant de l’aigua, quan augmenta la concentració d’ions oxoni, minva la d’hidroxils. La constant de l’aigua també varia amb la temperatura:
\[K_w=[H_3 O^+] \cdot [OH^-]=10^{-14}, pK_w=pH+pOH=14\]El pH fou definit el 1909 pel químic danès Søren Peter Lauritz Sørensen.
4. Àcids i bases febles
Un àcid feble és un àcid que té poca capacitat de cedir protons. Una base feble és una base que té poca capacitat d’acceptar-los (l’àcid acètic o l’àcid carbònic són àcids febles i l’hidròxid d’amoni és una base feble, per exemple).
Un àcid/ base forta és un àcid/base que té molta capacitat de cedir/acceptar protons (l’àcid sulfúric o clorhídric són àcids forts i l’hidròxid de sodi o de potassi són bases fortes, per exemple).
Si l’àcid (\[HA\]) és feble, la base conjugada (\[A^-\]) serà forta (tindrà molta capacitat per a acceptar protons).
En canvi, si l’àcid és fort, la base conjugada serà feble (tindrà poca capacitat per a acceptar protons).
\[HA \rightarrow A^- + H^+\]De la mateixa manera, si una base és feble, l’àcid conjugat serà fort i a l’inrevés.
Els àcids o bases febles tenen constants de dissociació més petites que la unitat. Són reaccions de dissociació reversibles. En canvi, els àcids o bases fortes tenen constants de dissociació grans i són pràcticament irreversibles.
La constant d’equilibri d’un àcid feble és:
Similarment, la d’una base feble és:
\[\displaystyle K_b=\frac{[B^+] \cdot [OH^-]} {[BOH]}\]Els claudàtors indiquen la concentració molar en l’equilibri de cada espècie.
A l’equilibri, la concentració d’ions hidrogen en un àcid és:
\[\displaystyle
[ H^+ ]=[ A^- ], [H A]=C_{inicial àcid }-[ H^+ ] \rightarrow [ H^+ ]=\sqrt{ K_a(C_{inicial àcid }-[ H^+ ])}
\]
Si la concentració d’ions hidrogen és petita comparada amb la concentració inicial de l’àcid sense dissociar-se:
\[[ H^+ ]=\sqrt{ K_a C_{inicial àcid}}
\\
[ HA ]~=C_{inicial àcid}
\]
(Vegeu l’entrada Equilibri Químic per a saber-ne més)
5. Efecte de l’ió comú
Com en qualsevol procés en equilibri, la ionització d’un àcid o d’una base feble pot estar influenciada per variacions de la concentració d’algun dels ions dissociats segons el principi de Le Chatêlier.
Per exemple, l’equilibri de la dissociació de l’àcid acètic es desplaçarà cap a l’esquerra si hi afegim ions acetat o un àcid, i es desplaçarà cap a la dreta si hi afegim una base.
Exemple:
\[\displaystyle{
\text{Quant minva la } H^+ \text{ d’una dissolució 0,20M d’àcid acètic quan s’hi afegeix NaAc 0,10M?}
\\
~K_a=1,8×10^{-5}
\\[0.5cm]
H^+= K_a \cdot { \frac{[HAc]} {~[Ac^-]} }=1,8×10^{-5}
\\[0.5cm]
\text{Abans d’afegir-hi NaAc, }[H^+]=[Ac^-]\text {:}
\\[0.5cm]
[H^+]^2= K_a \cdot {[HAc]}=1,8×10^{-5} \cdot 0,20=\sqrt {3,6×10^{-6}M}=1,90×10^{-3}M
\\[0.5cm]
\text{Després d’afegir-hi NaAc:}
\\[0.5cm]
H^+= K_a \cdot { \frac{[HAC]} {~[Ac^-]} }=1,8×10^{-5} \cdot { \frac{0,20} {0,10} }=3,6×10^{-6}M
\\[0.5cm]
\text{De fet, la concentració d’} AcH\text{ en l’equilibri és } 0.20+[H^+] \text{ i la d’ } [Ac^-]=0.10-[H^+],
\\
\text{ però podem fer l’aproximació anterior sense gaire error.}
}
\]
Exemple:
\[\displaystyle{
\text{Calculeu la concentració d’} H^+ \text{d’una dissolució formada per volums iguals d’HCl 0,10M}
\\
\text{i NaAc 0,40M.}
\\[0.5cm]
HCl \rightarrow H^+ (0,1M ) + Cl^-
\\
NaAc \rightarrow Na^+ + Ac^- ( 0,40M )
\\[0.5cm]
\text{Quan es barregen l’àcid clorhídric i l’acetat sòdic, 0,10mols de l’acid reaccionen amb}
\\
\text{ 0,10 mols de la sal i s’estableix l’equilibri:}
\\[0.5cm]
\begin{matrix}
Ac^- & + & H^+ & ⇌ & HAc \\
(0,40-0,10):2 & + & H^+ & ⇌ & 0,10:2\end{matrix}
\\
[ H^+]=K_a \cdot { \frac{[HAc]} {[Ac^-] }}=1,8×10^{-5} \cdot {\frac{0,050} {0,15}}=6,0×10^{-6}M
\\[0.5cm]
\text{Les concentracions en l’equilibri d’acetat i HAc s’han de dividir per dos perquè s’afegeixen}
\\
\text{volums iguals de cada reactiu.}
\\[0.5cm]
\text{De fet, }[ HAc ]=0,050-[H^+] \, i \, [ Ac^- ]=0,15+[H^+] \text{, però la concentració d’ions hidrogen és}
\\
\text{tan petita comparada amb la d’àcid i d’acetat que l’error que fem menyspreant-la}
\\
\text{és molt petit.}
}
\]
(Vegeu l’apartat 7. Hidròlisi d’aquest document)
6. Dissolucions amortidores, reguladores o tampó
Les dissolucions amortidores, reguladores o tampó són dissolucions el pH de les quals varia molt poc per dilució o addició de quantitats moderades d’àcids o de bases, fins i tot forts. Una solució està amortida, tamponada o regulada si s’oposa a la modificació de la concentració d’ions oxoni.
Estan formades per un àcid o una base feble i una de les seves sals fortament ionitzada.
Un compost que tingui a la vegada propietats àcides o bàsiques pot ser regulador de pH.
Per exemple, una dissolució de bicarbonat (\[HCO_3 ^-\]) té acció reguladora a causa d’aquest ió que pot cedir o acceptar protons quan reacciona amb altres àcids o bases:
H CO_3^- + OH^- ⇌ H_2 O + CO_3^{–}
\\
H CO_3^- + H^+ ⇌ H_2 CO_3
\]
En general, les sals d’àcids polipròtics febles tenen acció reguladora petita.
Exemple:
\displaystyle{
\text{La constant d’ionització d’un àcid feble és } K_a=1,0.10^{-5}.
\\
\text{Es preparen dues solucions 0,10M, una d’aquest àcid i l’altra de la seva sal sòdica.}
\\
\text{Calculeu el pH de la solució original i de la solució després d’afegir-hi 0,010 mols d’HCl }
\\
\text{i després d’afegir-hi 0,010 mols d’NaOH a un litre de solució reguladora.}
\\[0.5cm]
HA ⇌ H^+ + A^- \rightarrow [H^+]=K_a \cdot { \frac{[HA]}{ [A^-] }} \rightarrow pH=pK_a+log{\frac{[A^-]} {[HA]}}
\\[0.5cm]
\text{a) Abans d’afergir-hi l’àcid o la base:}
\\[0.5cm]
pH=pK_a+log{\frac{[A^-]} {[HA]}}=5+log{\frac{ 0,1 }{ 0,1 }}=5
\\[0.5cm]
\text{b) Després d’afegir-hi l’àcid l’equilibri es desplaçarà cap a l’esquerra:}
\\[0.5cm]
[ HA ]= 0,11, \, [ A^- ]=0,09 \rightarrow pH=pK_a+log{\frac{[A^-]}{[HA]}}=5+log{\frac{ 0,09 }{ 0,11 }}=4,91
\\[0.5cm]
\text{c) Després d’afegir-hi la base l’equilibri es desplaçarà cap a la dreta:}
\\[0.5cm]
[ HA ]= 0,09, \, [ A^- ]=0,11 \rightarrow pH=pK_a+log{\frac{[A^-]}{[HA]}}=5+log{\frac{ 0,11 } { 0,09 }}=5,09
}
\]
7. Hidròlisi
La hidròlisi és la descomposició d’una substància per l’acció de l’aigua sense transferència d’electrons. La sal d’un àcid feble i d’una base forta, la d’una base feble i d’un àcid fort i la d’un àcid i una base febles tenen tendència a hidrolitzar-se. Si és una reacció irreversible, la hidròlisi és completa:
\[PCl_3 + 3H_2 O \rightarrow 3HCl + H_3 PO_3\]Però si la reacció és reversible, com en el cas d’algunes sals, s’estableix un equilibri:
7.1 D’una reacció d’anions d’àcids febles
\[\displaystyle{
A^- + H_2 O ⇌ HA + OH^-
\\
K_{conjuagada}= \frac{[HA][OH^-]} {[A^-]}
}
\]
En una reacció d’hidròlisi intervenen dues reaccions d’equilibri, la \[A^-\] de la sal i la \[OH^-\] de l’aigua, les quals competeixen pels \[H^+\] :
\[\displaystyle{
HA ⇌ A^- + H^+
\\
H_2 O ⇌ OH^-+ H^+
\\[0.5cm]
K_a=\frac{[ H^+ ][A^-]} {[HA]} \rightarrow [ H^+ ]= K_a \cdot \frac{[HA]} {[A^-]} \, i,
\\
K_{H_2 O}=[ H^+ ][ OH^-] \rightarrow [ H^+ ]= \frac{K_{H_2 O}} {[ OH^-]}
\\
K_a \cdot \frac{[HA]} {[A^-]}=\frac{K_{H_2 O}} {[ OH^-]} \rightarrow [HA][ OH^-]=\frac{K_{H_2 O}} {K_a} [A^-]
\\
\text{Quan s’arriba a l ‘equilibri:} [HA]=[ OH^-] \rightarrow [ OH^-]=\sqrt{\frac{K_{H_2 O}} {K_a} [A^-]}
\\
pH=14-pOH
\\[0.5cm]
\text{O bé:}
\\[0.5cm]
K_{hidròlisi}=\frac{[HA][OH^-]} {[A^-][H_2 O]} \rightarrow K_{conjugda}=\frac{[HA][OH^-]} {[A^-]}
\\
[ OH^-]=\sqrt{K_{conjugada} \cdot [ A^- ]}=\sqrt{\frac {K_{H_2 O}} {K_a} \cdot [ A^- ]}
\\
pH=14-pOH
}
\]
7.2 D’una reacció de cations de bases febles
\[B^++H_2 O ⇌ BOH+ + H^+\]En aquest cas, \[B^+\] i els \[H^+\] de l’aigua competeixen pels \[OH^-\]:
\[\displaystyle{
BOH ⇌ OH^- +B^+
\\
H_2 O ⇌ OH^-+ H^+
\\[0.5cm]
[ H^+]=\sqrt{ K_{conjugada} \cdot [ B^+ ]}=\sqrt{\frac {K_{H_2 O}} {K_b} \cdot [ B^+ ]}
\\
pH=-log(\sqrt{\frac {K_{H_2 O}} {K_b} \cdot [ B^+ ]})
}
\]
8. Neutralització (Valoracions àcid-base)
La reacció entre un àcid i una base produeix una sal i aigua:
Hi ha diferents valoracions de neutralització depenent de la força de l’àcid i de la base.
Una valoració és possible si, l’error relatiu del canvi que indica el final de la reacció al volum de valorat, és de l’1 o el dos per mil (una o dues gotes -una gota=0,05 ml- de valorant en 50 ml de valorat).
És important saber el pH aproximat de neutralització d’una reacció per tal d’escollir bé l’indicador adequat.
En una reacció de neutralització:
En funció de la molaritat:
\[V_{valorant} \cdot (M_{valorant} \cdot \nu)=V_{valorat} \cdot (M_{valorat} \cdot \nu)\]\[\nu\] és el nombre d’equivalents gram de la substància.
(Vegeu MESCLES I BARREGES, 1.3 Concentració per a saber-ne més.)
8.1 D’un àcid fort i una base forta
La reacció en aquest cas és \[H^+ + OH^- ⇌ H_2 O\]. A la vora del punt estequiomètric, el canvi de pH és molt ràpid. La mesura del pH es fa amb un pH- metre o un potenciòmetre. El pH del punt final es pot detectar amb el canvi de color d’un indicador.
En una valoració sempre es compleix que:
\[N_{valorant} \cdot V_{valorant}=N_{valorat} \cdot V_{valorat}
\\
M_{valorant} \cdot \nu_{valorant} \cdot V_{valorant}=
M_{valorat} \cdot \nu_{valorat} \cdot V_{valorat}
\]
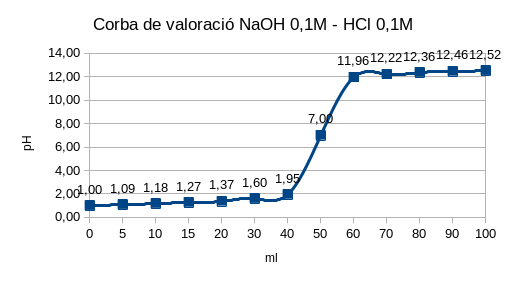
Exemple:
\displaystyle{
\text{Valoració de 50,00 ml de HCl 0,1 N amb NaOH 0,1 N -en aquest cas } \nu_{valorant}=\nu_{valorat}=1:
\\[0.5cm]
\text{A efectes de calcular el pH, la reacció és } H^+ + OH^-⇌ H_2 O
\\
\text{És a dir, que la concentració de NaOH és igual a la concentració d’} OH^-
\\
\text{i la concentració d’HCl és igual a la concentració d’H^+}
\\[0.5cm]
\text {a. Abans d’afegir la base:}
\\[0.5cm]
\text {Abans d’afegir la base el pH és el de la dissolució de clorhídric.}
\\
\text{Com que el clorhídric és un àcid fort, considerem que està}
\\
\text{completament dissociat. En aquest cas la normalitat és igual}
\\
\text{a la molaritat, i el pH=-log ( 0,1 )=1,00.}
\\[0.5cm]
\text {b. Quan s’han afegit 10,00 ml de NaOH:}
\\[0.5cm]
\text{Com que 1 meg (1 mol) de NaOH (OH^-) neutralitzarà 1 mol d´HCl} (H^+)
\\
\text{i el volum total de solució serà de 60,0 00 ml:}
\\[0.5cm]
[ H^+ ]=\frac{\text {mols HCl restants en dissolució}}{\text{Volum total dissolució}}
\\
\frac{\text{ mols HCl inicials – mols HCl neutralitzats}} {\text{Volum total dissolució}}=\frac{ 5-1 } {60 }=\frac{1}{15}M
\\
pH=-log[ H^+]=1.17
\\[0.5cm]
\begin {Bmatrix}
\text{mols HCl inicials}=0,1N \cdot 50,00ml=5 \\
\text{mols NaOH neutralitzats}=0,1N \cdot \text{V afegit NaOH}\\
\text{Volum total dissolució}=50,00ml+\text{V afegit NaOH}
\end {Bmatrix}
\\[1cm]
\text{3. En afegir-hi 25,00 ml de base:}
\\[0.5cm]
[ HCl ]= [H^+ ]\frac {\text{mols HCl restants en dissolució}} {\text{Volum total dissolució}}=
\\
\frac{\text{mols HCl inicials} – \text{mols HCl neutralitzats}} {\text{Volum total dissolució}}=\frac{ 5-2,5 } {75,00 }=\frac{1}{30}M
\\
pH=-log(1/30)=1.48
\\[0.5cm]
\begin {Bmatrix}
\text{mols HCl inicials}=0,1N \cdot 50,00ml=5
\\
\text{mols HCl neutralitzats}=0,1N \cdot \text{V afegit NaOH}=2,5 \text{ mols}
\\
\text{Volum total dissolució=50,00ml+V afegit NaOH}
\end {Bmatrix}
\\[1cm]
\text{4. En el punt estequiomètric:}
\\[0.5cm]
M_{HCl} \cdot V_{HCl}=M_{NaOH} \cdot V_{NaOH} \rightarrow V_{NaOH}=\frac{0.1M \cdot 50,00 ml}{0.1}=50,00 ml NaOH
\\
pH=7 ([H_3O^+]=[OH^-])
\\[1cm]
\text{5. Després del punt estequiomètric: es calcula el pH per l’excés de NaOH afegit.}
\\
\\ \text{Havent afegit 60,00 ml de NaOH:}
\\
pH=14-pOH=14+log(\frac{0.1 \cdot 10.00 \enspace ml}{110\enspace ml})=12
\\
\\
\text{Els càlculs de la valoració d’una base feble amb un àcid fort són similars als anteriors.}
}
\]

 RSS CEEdukat
RSS CEEdukat

Quant a l'autor