1. Definició
La programació lineal és la part de les matemàtiques que determina el valor de les variables restringides \[x, y\] d’una funció \[f(x,y)\] que es vol maximitzar o minimitzar. La funció i les restriccions són funcions lineals.
A batxillerat, també s’estudia com fer l’optimització de funcions no lineals de dues variables.
(Vegeu també l’entrada Inequacions per a saber-ne més)
2. Resolució
Els passos per a resoldre els exercicis de programació lineal són:
- Es llegeix atentament l’exercici per tal de plantejar l’equació de la funció i el sistema d’inequacions de les restriccions.
- S’escriu l’equació de la funció que es vol optimitzar i les inequacions de les restriccions: la pregunta de l’exercici ens indica quines són les variables que hem de calcular. Per tant, assignarem les incògnites \[x,y\] a aquestes variables per a construir la taula de restriccions.
- Dibuixem la regió factible delimitada pel sistema d’inequacions.
- Calculem els vèrtexs de la regió factible.
- Introduïm el valor de cada vèrtex a la funció i en calculem el valor.
- Determinem el valor de la funció més gran (màxim) o més petit (mínim).
Exemple (PAU juny 2001):
En un taller de confecció es disposa de 80 metres quadrats de tela de cotó i de 120 metres quadrats de tela de llana. Es fan dos tipus de vestits, A i B. Per fer un vestit del tipus A es necessita 1 metre quadrat de cotó i 3 metres quadrats de llana; en canvi, per un vestit del tipus B calen 2 metres quadrats de cada tipus de tela.
a) Quants vestits de cada tipus s’han de fer per obtenir un benefici total màxim si per cada vestit (sigui del tipus que sigui) es guanyen 30 euros?
b) Quina seria la conclusió a la pregunta anterior si per cada vestit del tipus A es guanyen 30 euros i, en canvi, per cada un del tipus B només es guanyen 20 euros.
2.
Nombre de vestits A: \[x\]
Nombre vestits B: \[y\]
Funció objectiu: \[f(x,y)=30x+30y\]
Taula de restriccions:
| A | B | m² | |
|---|---|---|---|
| Llana | \[3x\] | \[2y\] | \[\leq 120\] |
| Cotó | \[1x\] | \[2y\] | \[\leq 80\] |
3.
Per a delimitar la regió factible, dibuixarem la funció lineal de cada inequació.
Cada funció divideix el pla en dos semiplans. Per a determinar quin és el semiplà solució, substituirem un punt qualsevol del pla en la inequació. El punt que triem no ha de ser un punt de les rectes de les inequacions. Normalment agafem el (0,0) per comoditat de càlcul.
Si es compleix la inequació, el semiplà solució és el pla al qual pertany el punt anterior, sinó és l’altre.
Farem el mateix procediment per a cada inequació. La regió comuna als semiplans és la regió factible.
Exemple:
\[x+2y \leq 80\\
0+2 \cdot 0=0\\
0 \leq 80\\[1cm]
3x+2y \leq 120\\
3 \cdot 0+2 \cdot 0=0\\
0 \leq 120\\
\]
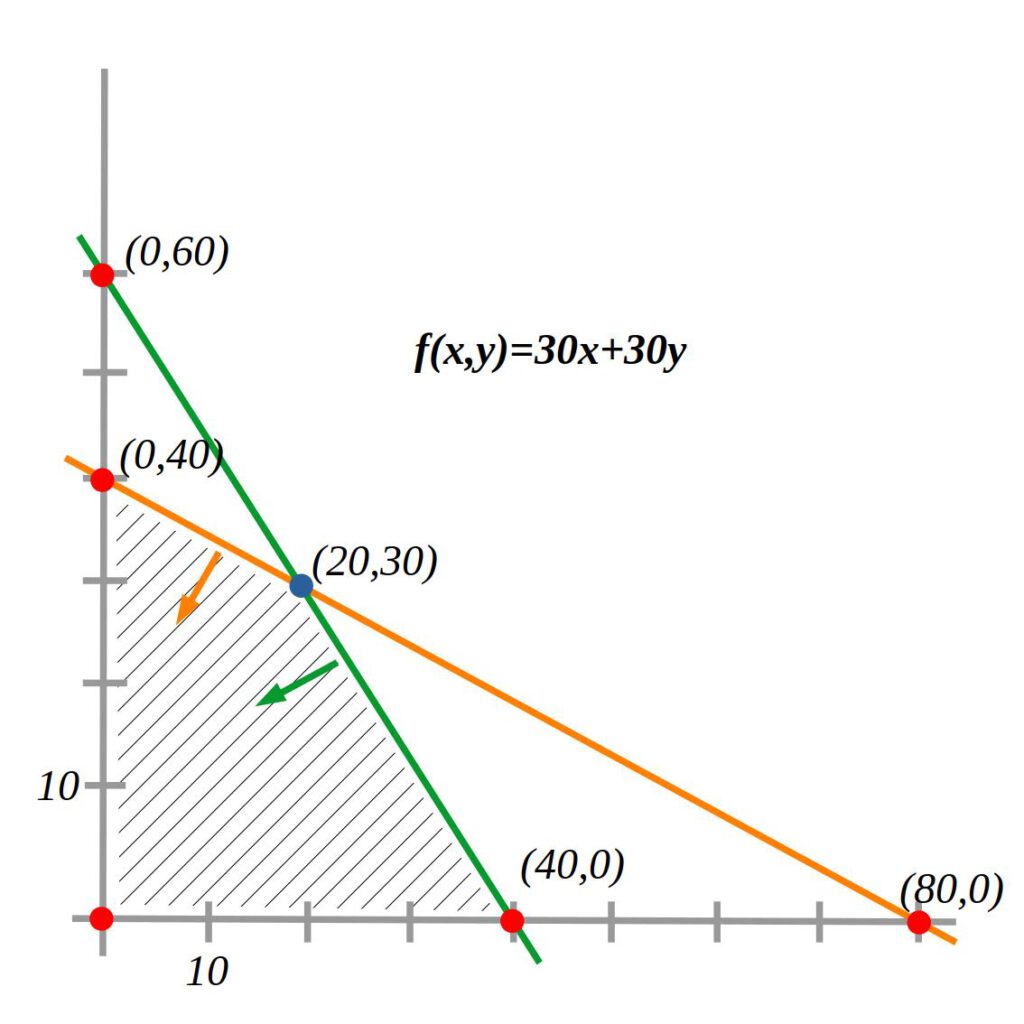
4.
Per a calcular el vèrtex de color blau, fem el sistema d’equacions:
\[
y=\frac{80-x}{2}=\frac{120-3x}{2}\\
2(80-x)=2(120-3x)\\
80-120=-3x+x\\
2x=40\\
x=20\\[1cm]
y=\frac{80-x}{2}\\
y=30
\]
5.
\[f(40,0)=30.40+30.0=1 200\\
f(0,40)=30.0+30.40=1 200\\
f(20,30)=30.20+30.30=\textbf {1 500}
\]
6. El punt que maximitza la funció és el \[\textbf {(20,30).}\]
La solució de l’apartat b) és:
\[f(x,y)=30x+20y\\[0.5cm]
f(40,0)=30.40+20.0=1 200\\
f(0,40)=30.0+20.40=800\\
f(20,30)=30.20+20.30=\textbf {1 200}
\]
6. El punt que maximitza la funció és també el \[\textbf {(20,30).}\]

 RSS CEEdukat
RSS CEEdukat

Quant a l'autor