Derivades

1. Definició

La derivada d’una funció en un punt és el valor del pendent de la recta tangent en aquest punt.

El pendent o la inclinació (\[\varphi\]) de la línia de color blau (taxa de variació mitjana) és \[\frac{y_2-y_1}{x_2-x_1}\].

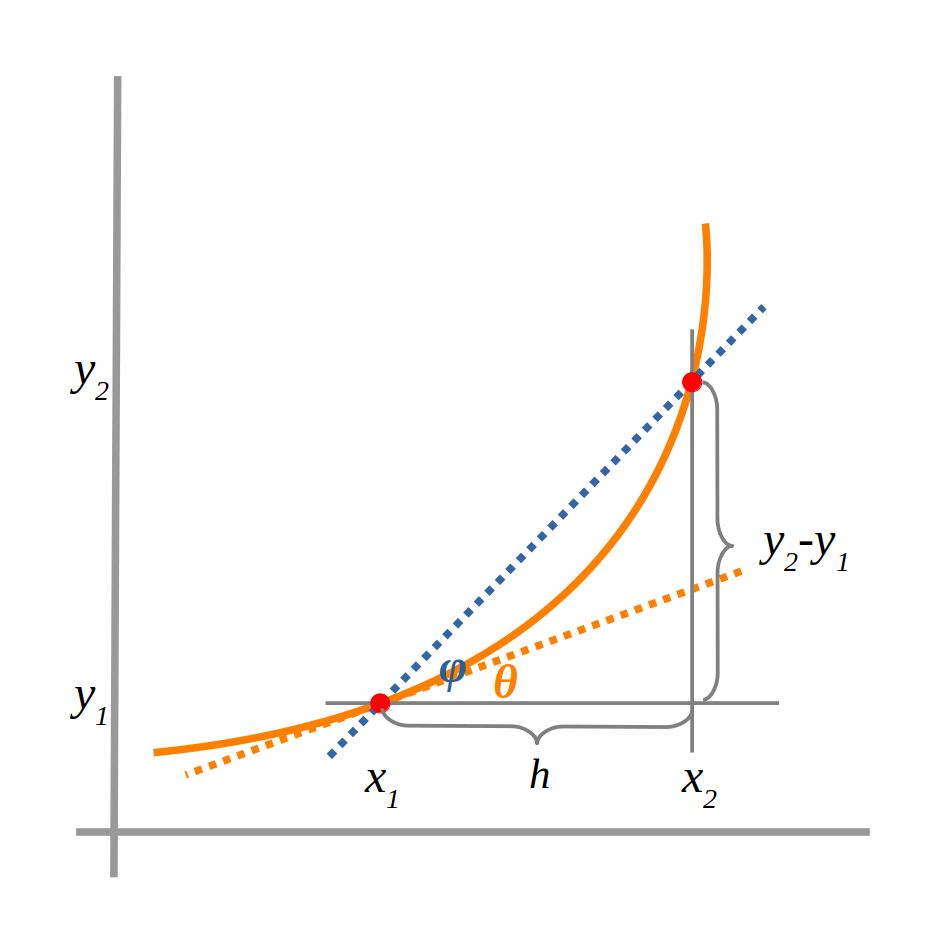
Però aquesta inclinació no coincideix amb la inclinació de la recta tangent en el punt de tangència \[x_1\] (línia de color carabassa). Les inclinacions coincidiran quan la diferència entre \[x_2\] i \[x_1 \enspace (h)\] sigui infinitament petita.

\[
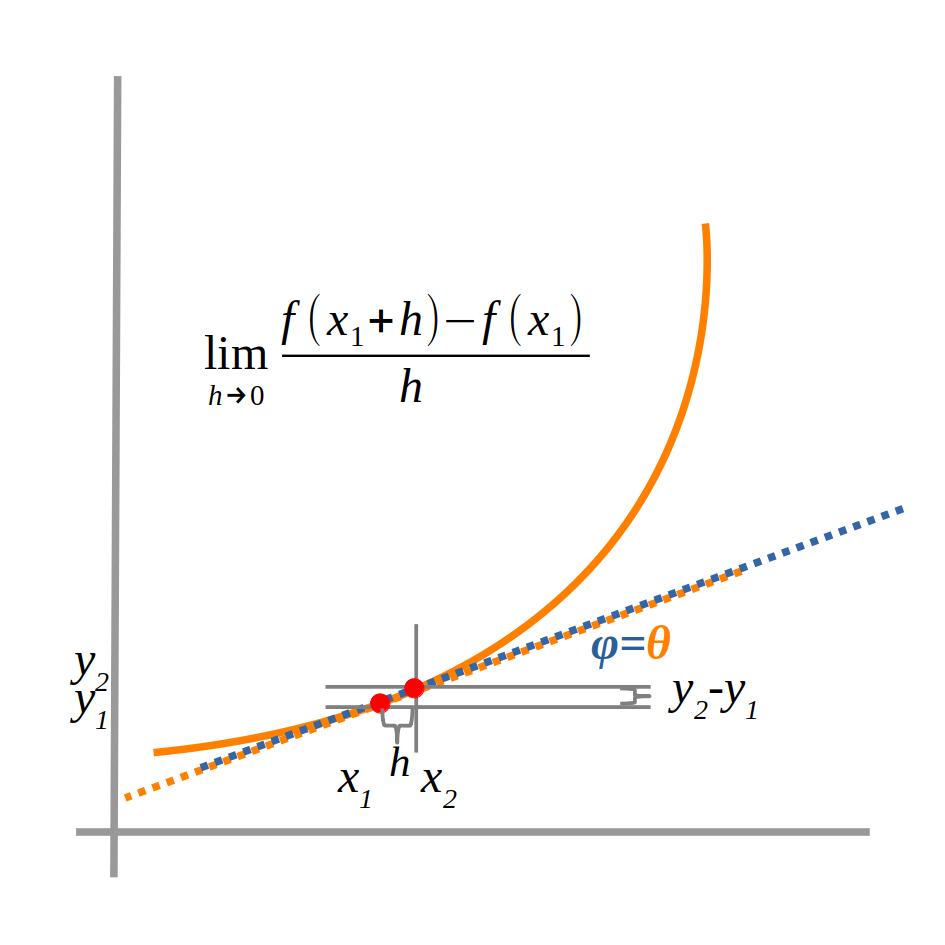
lim_{h\to 0}\frac{y_2-y_1}{x_2-x_1}=lim_{h\to 0}\frac{y_2-y_1}{(x_1+h)-x_1}=lim_{h\to 0}\frac{f(x_1+h)-f(x_1)}{h}=lim_{h\to 0}\frac{f(x+h)-f(x)}{h}
\]

Ara bé, si introduïm cadascuna de les funcions elementals en el la fórmula de la definició de derivada anterior i fem els càlculs necessaris, el resultat que obtenim és la funció derivada. La funció derivada és la funció que ens informa del pendent de la funció primitiva o sense derivar en qualsevol punt.

Exemple:

\[
\textbf{y=x²}
\\
lim_{h\to 0}\frac{f(x+h)²-f(x²)}{h}
\\
lim_{h\to 0}\frac{f(x+h)²-f(x²)}{h}
\\
lim_{h\to 0}\frac{x²+2xh+h²-x²}{h}
\\
lim_{h\to 0}\frac{h(2x+h)}{h}
\\
lim_{h\to 0}{2x+h}=2x
\\
\textbf {y’=2x}
\]

D’aquesta manera, obtenim la taula de derivades de les funcions elementals:

\[f(x)\]	\[f'(x)\]
\[y=k\]	\[y’=0\]
\[y=x\]	\[y’=1\]
\[y=kx\]	\[y’=k\]
\[y=x^n\]	\[y’=nx^{(n-1)}\]
\[y=\ln x\]	\[y’=\frac{1}{x}\]
\[y=e^x\]	\[y=e^x\]
\[y=\log_a x\]	\[y’=\frac{1}{x.ln a}\]
\[y=a^x\]	\[y=a^x. \ln a\]
\[y=\sin x\]	\[y’=\cos x\]
\[y=\cos x\]	\[y’=-\sin x\]
\[y=\tan x\]	\[y’=sec²x\]
\[y=\arcsin x\]	\[y’=\frac{1}{\sqrt{1-x²}}\]
\[y=\arccos x\]	\[y’=-\frac{1}{\sqrt{1-x²}}\]
\[y=\arctan x\]	\[y’=\frac{1}{1+x²}\]

2. Propietats de les derivades:

Les propietats de les derivades són:

a) Derivada d’una suma/ diferència de funcions: \[[f(x)+g(x)]’=f'(x)+g'(x)\]

b) Derivada d’un producte de funcions: \[[f(x) \cdot g(x)]’=f'(x) \cdot g(x)+f(x) \cdot g'(x)\]

c) Derivada d’un quocient de funcions: \[[\frac{f(x)}{g(x)}]’=\frac{f'(x) \cdot g(x)-f(x) \cdot g'(x)}{[g'(x)]²}\]

3. Regla de la cadena

Si \[f(x)\] i \[g(x)\] són dues funcions derivables i \[h(x)\] és la funció composta d’aquestes dues funcions, la derivada d’ \[h(x)=f(x) ∘ g(x)= f[g(x)]\] és \[h'(x)=f'[g(x)] \cdot g'(x)\].

Exemple:

\[
f(x)=\sin x,g(x)=x²+2
\\
h(x)=f(x) ∘ g(x)=f[g(x)]=sin(x²+2)
\\
h'(x)=f'[g(x)] \cdot g'(x)=[\sin (x²+2)]’ \cdot (x²+2)’=cos(x²+2) \cdot 2x
\]

Per tant, la taula de derivades d’una funció composta és:

\[h(x)\]	\[h'(x)\]
\[y=k\]	\[y’=0\]
\[y=k \cdot h(x)\]	\[y’=k \cdot h'(x)\]
\[y=h(x)^n\]	\[y’=n \cdot h(x)^{n-1} \cdot h'(x)\]
\[y=\ln h(x)\]	\[y’=\frac{h'(x)}{h(x)}\]
\[y=e^{h(x)}\]	\[y=e^{h(x)} \cdot h'(x)\]
\[y=\log_a h(x)\]	\[y’=\frac{h'(x)}{h(x).ln a}\]
\[y=a^{h(x)}\]	\[y=a^{h(x)} \cdot \ln a \cdot h'(x)\]
\[y=\sin h(x)\]	\[y’=\cos h(x) \cdot h'(x)\]
\[y=\cos h(x)\]	\[y’=-\sin h(x) \cdot h'(x)\]
\[y=\tan h(x)\]	\[y’=sec²h(x) \cdot h'(x)\]
\[y=\arcsin h(x)\]	\[y’=\frac{h'(x)}{\sqrt{1-h²(x)}}\]
\[y=\arccos h(x)\]	\[y’=-\frac{h'(x)}{\sqrt{1-h²(x)}}\]
\[y=\arctan h(x)\]	\[y’=\frac{h'(x)}{1+h²(x)}\]

4. Aplicacions de les derivades

4.1 Monotonia i punts crítics d’una funció

La monotonia d’una funció es refereix al creixement i decreixement de la funció en cada interval del domini.

Els punts crítics d’una funció són els punts que anul·len la primera derivada (\[y’=0\]). Aquests punts són els possibles màxims, mínims i punts d’inflexió de la funció.

4.1.1 Monotonia, màxims i mínims

Els màxims i mínims són els punts en els quals canvia la monotonia o creixement de la funció.

El punt en el qual la monotonia de la funció canvia de decreixent a creixent, és un mínim. En aquest punt, la inclinació o pendent és zero, abans d’aquest punt és negativa i després és positiva.

Exemple:

\[
y=x²+4x+4\\
y’=2x+4=0\\
x=-2\\
y(-2)=(-2)²+4(-2)+4=0\\
\textbf {Mínim(-2,0)}
\]

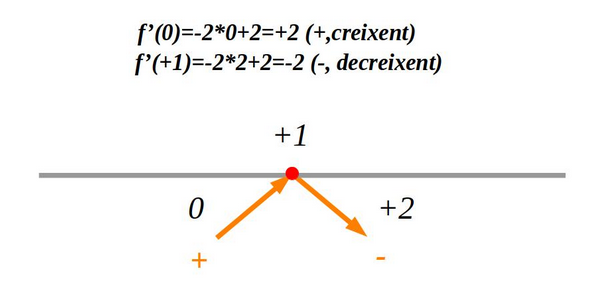
El punt en el qual la monotonia de la funció canvia de creixent a decreixent, és un màxim. En aquest punt, la inclinació o pendent és zero, abans d’aquest punt és positiva i després és negativa.

\[
y=-x²+2x\\
y’=-2x+2=0\\
x=1\\
y=-(1)²+2 \cdot 1=1\\
\textbf{(1,1)}
\]

4.1.2 Curvatura i punts d’inflexió

Els punts d’inflexió són els punts en els quals canvia la curvatura de la funció. La curvatura indica el canvi de direcció de les tangents d’una funció entre dos punts de tangència.

La curvatura en un interval és positiva si la la gràfica de la funció està per sobre la de la recta tangent.

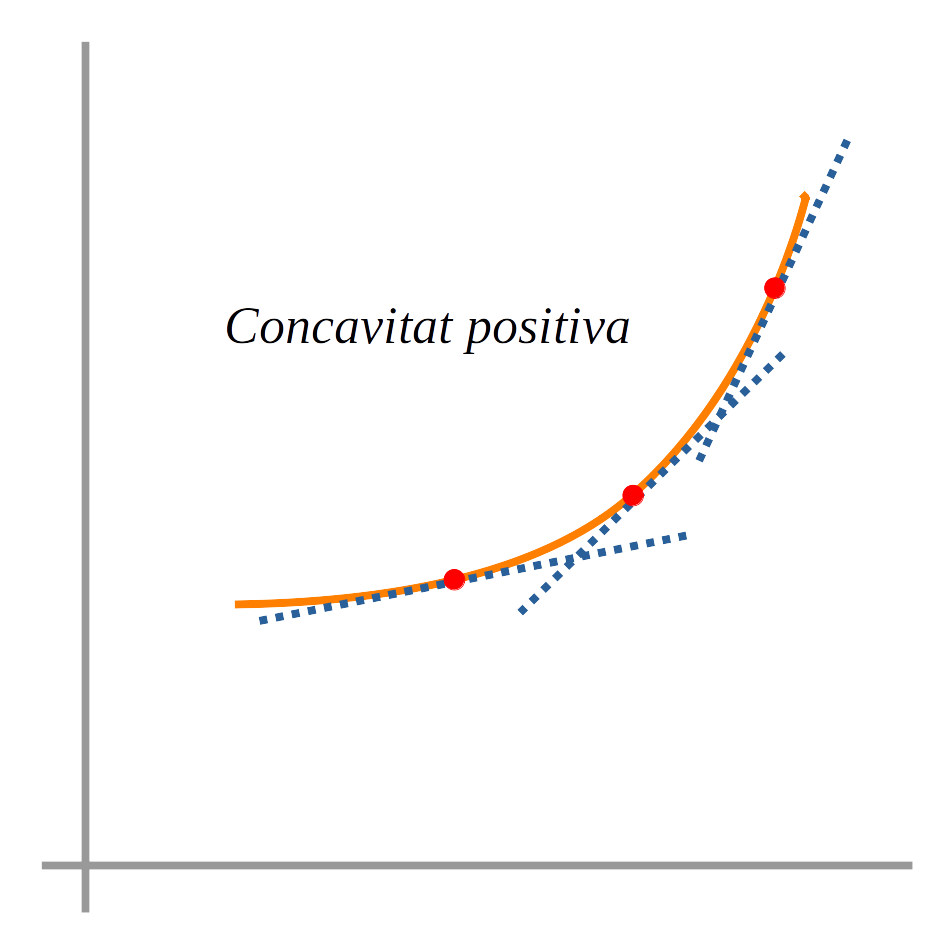
La curvatura en un interval és negativa quan la gràfica de la funció està per sota de la recta tangent.

Si una funció té curvatura positiva en un interval, tindrà un punt mínim en aquest interval. Si una funció té curvatura negativa en un interval, tindrà un màxim en aquest interval.

Per a determinar els punts d’inflexió, farem la segona derivada igual a zero \[y”=0\]. Si hi ha un canvi de signe (concavitat) en un punt, aquest punts és un punt d’inflexió.

Exemple:

\[
y=x³-3x²-5x+8
\\
y’=3x²-6x-5
\\
y”=6x-6=0
\\x=1
\]

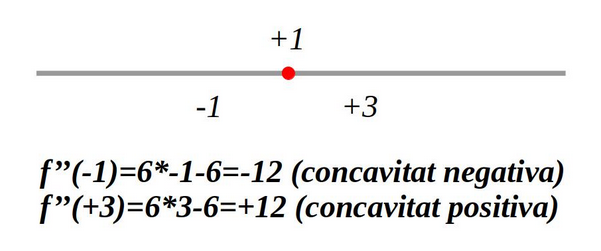
Una altra manera de determinar si un punt singular és un màxim o un mínim, es fent la segona derivada i determinant el signe en aquest punt: si és positiu serà un mínim i si és negatiu serà un màxim.

Exemple:

\[
y=x²+4x+4 \rightarrow y’=2x+4 \rightarrow y”=2 \enspace \text{(convavitat positiva: mínim)}
\\
y=-x²+2x \rightarrow y’=-2x+2 \rightarrow y”=-2 \enspace \text{(concavitat negativa: màxim)}
\\
\]

4.2 Recta tangent

Una altra aplicació de les derivades és trobar l’equació de la recta tangent en un punt.

Per a resoldre exercicis de la recta tangent farem:

1. La primera derivada de la funció
2. Si en donen la \[m\] trobarem \[x_0\]. Si ens donen \[x_0\] trobarem la m.
3. Calcularem \[y_0\] substituint \[x_0\] a l’equació \[y=f(x)\]
4. Escriurem l’equació de la recta tangent.

Exemple:

\[
y=x²+6x-6, \enspace m=2\\
1. y’=2x+6=m\\
2. 2x_0+6=2 \rightarrow x_0=-2\\
3. y_0=(x_0)²+6x_0-6=(-2)²+6*(-2)-6=-14\\
4. y-y_0=m*(x-x_0) \rightarrow \textbf {y+14=2*(x+2)}\\
\]

\[
y=x²+6x-6, \enspace x_0=-2\\
1. y’=2x_0+6=m\\
2. m=2*-2+6=2\\
3. y_0=(x_0)²+6x_0-6=(-2)²+6*(-2)-6=-14\\
4. y-y_0=m*(x-x_0) \rightarrow \textbf {y+14=2*(x+2)}\\
\]

4.3 Optimització

És trobar els valors de les variables de la funció objectiu (funció que es vol maximitzar o minimitzar) tenint en compte les restriccions (limitació dels valors de les variables).

Per a resoldre els exercicis d’optimització farem:

1. Analitzant la geometria plantejarem l’equació de la funció objectiu i de la restricció.
2. Aïllarem una de les incògnites de la restricció (la que faci els càlculs posteriors més senzills) i la substituïrem a la función objectiu.
3. Farem la primera derivada de la funció objetiu i la igualarem a zero.
4. Resoldrem l’equació que en resulti.
5. Substituint el resultat a la restricció trobarem el valor de la segona incògnita.
6. Calcularem el valor de la funció objectiu.
7. Determinarem si és un màxim o un mínim.

Exemple:

Hem de determinar quins valors de la longitud dels catets d’un triangle rectangle fan que l’àrea sigui màxima tenint en compte que la hipotenusa ha de fer 12 unitats de longitud:

\[
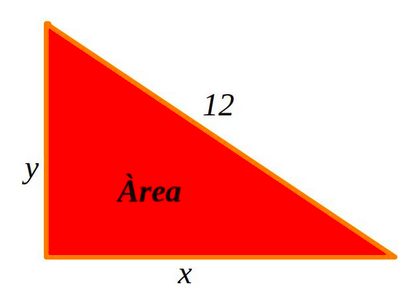
1.\\
A=\frac {x*y}{2} \enspace \text{(funció objectiu)}\\
h²=x²+y² \enspace \text{(restricció)}\\
2.\\
x=\sqrt{h²-y²}\\
A=\frac{\sqrt{h²-y²}*y}{2}\\
3.\\
A’=-\frac{2y²}{4*\sqrt{h²-y²}}+\frac{\sqrt{(h²-y²)}}{2}=0\\
4.\\
-\frac{2y²}{\sqrt{h²-y²}}+\sqrt{(h²-y²}=0\\
\frac{y²}{2*\sqrt{h²-y²}}=\frac{\sqrt{(h²-y²}}{2}\\
y²=(h²-y²)\\
y=\frac{h}{\sqrt2}=\frac{12}{\sqrt{2}}\approx 8.5\\
5.\\
x=\sqrt{h²-y²}=\sqrt{12²-(\frac{12}{\sqrt 2})²}=\frac{12}{\sqrt{2}}\approx 8.5\\
6.\\
A=\frac{\frac{12}{\sqrt{2}} * \frac{12}{\sqrt{2}}}{2}=38u²\\
7.A'(8)>0,A'(9)<0 \enspace \text{(és un màxim).}
\]