Arxiu d'etiquetes vectors

Instruccions abans de començar

1. Definició

Un vector (\(\vec{v}\)) és un segment orientat. Per a definir un vector ens calen dos punts: un punt d’origen i i el punt de l’extrem. Un vector del pla té dos components, l’horitzontal i el vertical, que representen les unitats que s’han de desplaçar per anar de l’origen a l’extrem del vector.

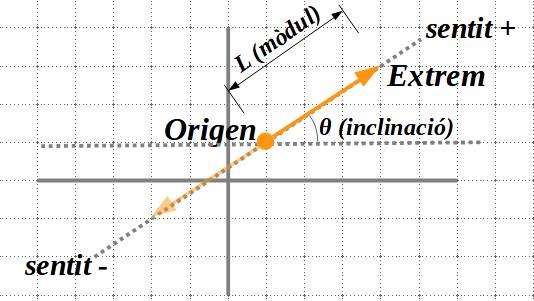
A diferència d’un escalar (un nombre), un vector té quatre característiques:

(i) Mòdul (\(\left|\vec{v}\right|\)): és la longitud del segment. Per a calcular el módul d’un vector fem: \(\left|\vec{v} \right|=\sqrt{v_1^2+v_2^2}\) unitats.

Exemple:

\(\left|(3,1) \right|=\sqrt{3^2+1^2}=\sqrt{10}\) unitats.

(ii) Direcció (\(\theta\)): és la inclinació o el pendent de la recta sobre la qual està situat el vector. Dos vectors tenen la mateixa direcció si estan sobre rectes paral·leles o coincidents.

La direcció o inclinació d’un vector és l’arc tangent del component vertical del vector dividit per l’horitzontal: \(\arctan \frac{y}{x}\)-.

Exemple:

\(\alpha=\arctan\frac{1}{3}= 18.43º\)

(Vegeu l’entrada raons trigonomètriques per a saber-ne més).

(iii) Sentit: és cap a on apunta la fletxa. Pot ser positiu o negatiu.
(iv) Origen: és el punt d’on surt el vector.

2. Operacions amb vectors

2.1 Suma/resta

\(
\vec{u} = (u_{1}, u_{2}), \vec{v} = (v_{1}, v_{2})
\\
\vec{u} + \vec{v} = (u_{1}+ v_{1},u_{2}+v_{2})
\\
\vec{u} – \vec{v} = (u_{1}- v_{2}, u_{2}- v_{2})
\)

Exemple:

\(
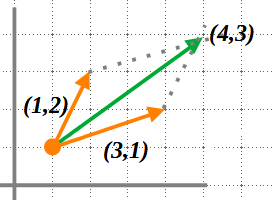
\vec{u} = (3,1),\, \vec{v} = (1,2)\\
\vec{u} + \vec{v} = (3,1)+(1,2)=(4,3)\\
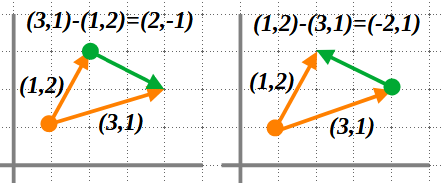
\vec{u} – \vec{v} = (3,1)-(1,2)=(2,-1)\\
\vec{v} – \vec{u} = (1,2)-(3,1)=(-2,1)\\
\).

2.2 Multiplicació

2.2.1 D’un vector per un escalar

Quan multipliquem un vector per un escalar el resultat és un altre vector paral·lel amb una longitud (mòdul) de \(k\) vegades.

\(k*\vec{v} = k*(v_{1}, v_{2}) = (k*v_{1}, k*v_{2})\)

Exemple:

\(k = -4*(3,-6) = (-12,24)\)

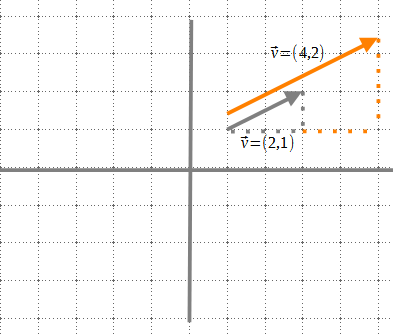
El component horitzontal del vector gris és de dues unitats i el vertical d’una. Al multiplicar-lo per dos, el component horitzontal del vector resultant és quatre i el vertical de dos.

2.2.2 Producte escalar de dos vectors

El producte escalar o producte punt de dos vectors és una multiplicació entre dos vectors que dóna com a resultat un escalar (nombre):

\(\vec{u}\cdot\vec{v} = (u_{1}, u_{2})\cdot(v_{1}, v_{2}) = u_{1}*v_{1} + u_{2}*v_{2}\)

Exemple:

\((3,1)\cdot (2,-4)=(3*2+1*-4)= 2\)

Una altra manera de calcular el producte escalar entre dos vectors és:

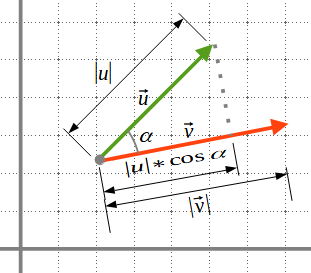
\(\vec{u}\cdot \vec{v} =\left|\vec{u}\right|*\left|\vec{v}\right|*\cos\alpha\)

(\(\alpha\) és l’angle que formen els vectors.)

Exemple:

\(
\vec{u}=(3,1), \, \vec{v}=(2,-4), \ \alpha=81.87º \\
(3,1)\cdot(2,-4)=\left|(3,1) \right|*\left|(2,-4) \right|*cos{81.7}=\sqrt{10}*\sqrt{20}*cos{\,81.87}= 2\)

El producte escalar de dos vectors és el resultat de multiplicar un dels vectors per la projecció horitzontal de l’altra sobre el primer.

2.3 Angle entre dos vectors

Per a calcular l’angle que formen dos vectors, fem servir la definició anterior de producte escalar :

\(
\cos{\alpha} = \frac{\vec{u}\cdot\vec{v}}{\left| \vec{u} \right|*\left|\vec{v} \right|} \Rightarrow
\alpha=\arccos(\frac{\vec{u}\cdot\vec{v}}{\left|\vec{u} \right|*\left|\vec{v}\right|} )
\)

Exemple:

\(\alpha=\arccos{\frac{2}{\sqrt{10}* \sqrt{20}}}= 81.87º\)

(Vegeu l’entrada raons trigonomètriques per a saber-ne més).

El producte escalar de dos vectors perpendiculars és zero perquè \(\cos{\, 90º} =0\).

El producte escalar compleix les següents propietats:

(i) Commutativa: \(\vec{u}\cdot\vec{v} = \vec{v}\cdot\vec{u}\).
(ii) Distributiva: \(\vec{w}\cdot(\vec{u}+\vec{v}) = \vec{w}\cdot\vec{u} + \vec{w}\cdot\vec{v}\)
(iii) El producte escalar d’un vector per ell mateix és el seu mòdul al quadrat: \(\vec{v}\cdot\vec{v} = \left|\vec{v} \right|*\left|\vec{v} \right|*\cos0 = |\vec{v}|^2\).

3. Combinació lineal de vectors

Si un vector \(\vec{w}\) és combinació lineal d’un altre són dos vectors proporcionals: \(\vec{w} = k*\vec{v}\). Un vector \(\vec{w}\) és combinació lineal de dos vectors diferents si \(\vec{w} = \mu*\vec{u} + \lambda*\vec{v}\).

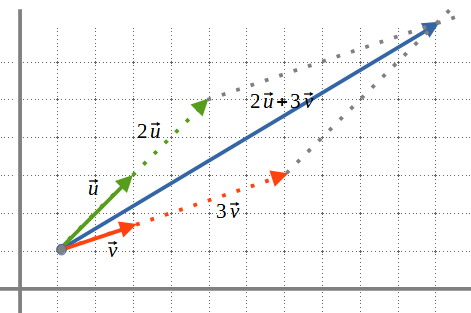
Quan en un conjunt de vectors cap vectors es pot obtenir com a combinació lineal d’altres vectors diem que aquests vectors són linealment independents. La condició perquè un conjunt de vectors siguin linealment independents és:

\(\lambda_1*\vec{v_1}+\lambda_2*\vec{v_2}+…\lambda_n*\vec{v_n}=0\), sols si tots els coeficients \(\lambda\) són zero.

4. Bases

Una base són un conjunt de vectors linealment independents que poden generar tots els altres vectors del pla o de l’espai. És a dir, que qualsevol altre vector és una combinació lineal d’aquests vectors.

Al pla, dos vectors \(\vec{v_1},\vec{v_2}\) si són linealment independents i poden generar tots els altres vectors del pla ( \(B ={\vec{v_1},\vec{v_2}}\)):

\(\vec{w}=\lambda_1*\vec{v_1}+\lambda_2*\vec{v_2}\), essent \(\vec{v_1}, \,\vec{v_2}\) linealment independents.

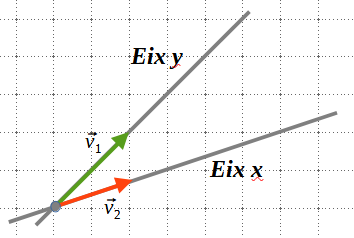
3.1 Base ortogonal

Una base de vectors és ortogonal si els vectors que la formen són perpendiculars entre sí.

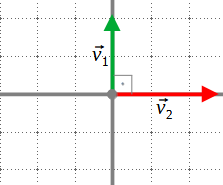
3.2 Base ortonormal

Un vector unitari (\({\hat{v}}\)) és un vector de mòdul \(1\): \(\hat v=\frac{\vec v}{\left ||v \right ||}\)

Per a normalitzar un vector dividim cada component pel seu mòdul:

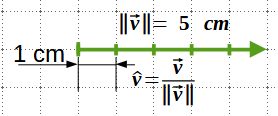
Exemple:

\(\widehat{(5,-9)}=\frac{(5,-9)}{\sqrt{5^2+(-9)^2}}=(\frac{5}{\sqrt{106}},\frac{-9}{\sqrt{106}})\)

Quan els vectors de la base són ortogonals i normals, és una base ortonormal.

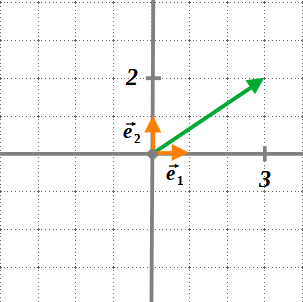
Els vectors \((1,0)\) i \((0,1)\) formen la base ortonormal del pla \(B={\vec{e_1}(1,0),\, \vec{e_2}(0,1)}\).

Qualsevol vector del pla és una combinació lineal d’aquests dos vectors: \(\vec{w_1}=\lambda_1*\vec{e_1}+4\lambda_2*\vec{e_2}\)

Exemple:

\((3,2)=3*\vec{e_1}+2*\vec{e_2}\)

3.3 Coordenades d’un vector

Les coordenades d’un vector en una base són els coeficients \(\lambda_n\) del vector expressat en aquesta base.

En l’exemple anterior, les coordenades del vector (3,2) en base ortonormal expressat en la base \(B=\left\{ (5,7), (6,2) \right\}\) és el vector \((\frac{3}{16}, \, \frac{11}{32})\):

Exemple:

\(
(3,2)=\lambda_1*(5,7)+\lambda_2*(6,2) \\
3=5*\lambda_1+6*\lambda_2\ \\
2=7*\lambda_1+2*\lambda_2 \\
\lambda_1= \frac{3}{16} \\
\lambda_2= \frac{11}{32} \\
\)

5. Sistemes de referència

Un sistema de referència és el conjut format per una base de vectors \(\vec{u},\vec{v}\) i un origen de coordenades \(O\): \(R = {O,[\vec{u},\vec{v}]}\).

En un sistema de referència a cada punt \(P\) del pla se li associa un vector de posició \(OP\).

(Vegeu Vectors en l’espai per a saber-ne més).