1. Equacions de la recta
(Vegeu Vectors en el pla per a saber-ne més.)
1.1 Definició
Una recta és un conjunt de punt infinits en línia. Podem definir una recta amb dos punts o amb un punt i un pendent.
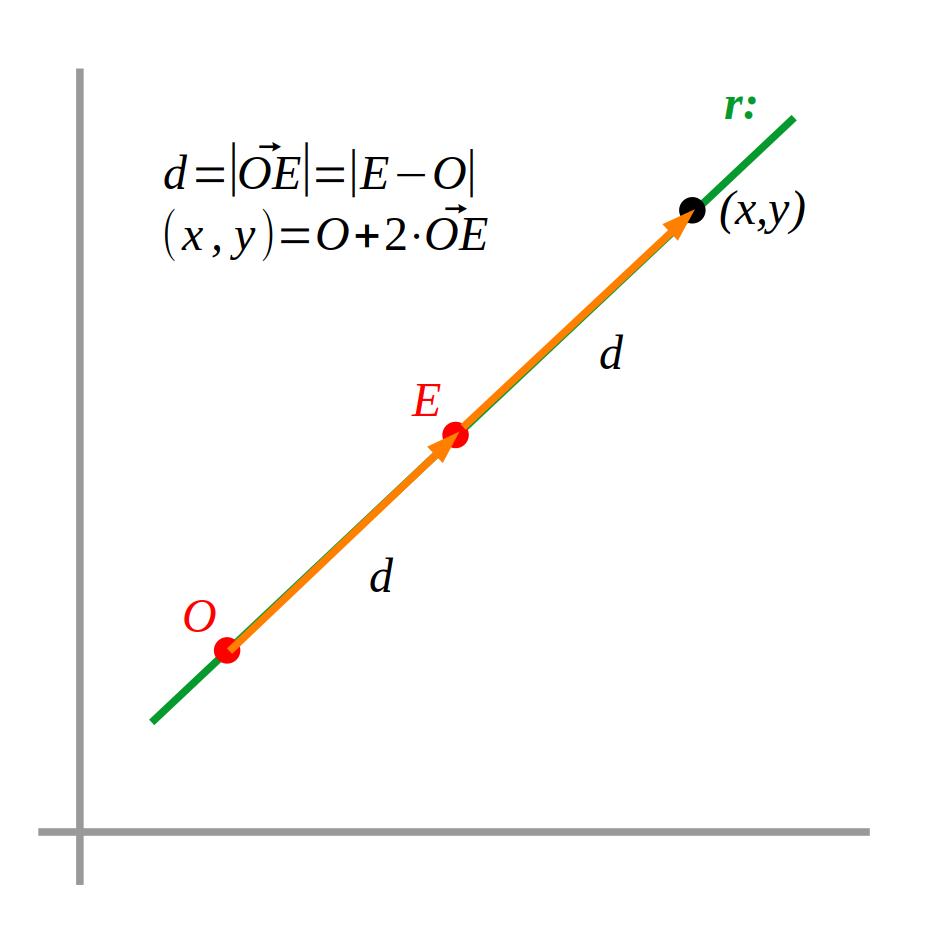 punt-punt
punt-punt punt -pendent
punt -pendent
1.2 Equacions de la recta
L’equació d’una recta es pot expressar de diferents maneres. Farem sevir l’equació que més ens convingui per tal de fer els càlculs més fàcilment o segons les dades disponibles.
1.3 Equació vectorial
L’equació vectorial de la recta es dedueix de la definició d’una recta amb dos punts: si a un punt d’origen de la recta que volem definir li sumem un nombre determinat de vegades (\(t\)) un dels vectors directors de la recta podem trobar-ne qualsevol altre punt.
\((x,y)=(x_0,y_0) + t \cdot (u,v)\)
1.4 Equació paramètrica
Igualant els components \(x\) i \(y\) de l’equació vectorial:
\(
x=x_0+t \cdot u\\
y=y_0+ t \cdot v
\)
1.5 Equació contínua
Aïllant el paràmetre \(t\) de cadascuna de les equacions paramètriques anteriors:
\(
t=\frac{x-x_0}{u}=\frac{y-y_0}{v}
\)
1.6 Equació general o implícita
Surt de fer el producte d’extrems i de mitjos de l’equació contínua:
\(
v \cdot (x-x_0)=u \cdot (y-y_0)\\
v \cdot x-v \cdot x_0=u \cdot y-u \cdot y_0\\
v \cdot x-u \cdot y-v \cdot x_0+u \cdot y_0=0\\
A=v, \, B=-u, \, C=-v \cdot x_0+u \cdot y_0\\
Ax+By+C=0
\)
El vector \(\vec{n}=(A,B)\) és un dels dos vectors perpendiculars de la recta. Per a calcular el vector perpendicular d’una recta tan sols hem de permutar els components del vector i canviar-ne un de signe.
Els vectors perpendiculars de dues rectes formen el mateix angle que els vectors directors.
Exemple:
\(\vec{v}=(9,-6) \rightarrow \vec{n_1}=(6,9), \enspace \vec{n_2}=(-6,-9)\).
1.7 Equació explícita
Aïllant la \(y\) de l’equació general:
\(
y=-\frac{A}{B} \cdot x-\frac{C}{B}\\
m=-\frac{A}{B}, \, n=-\frac{C}{B}\\
y=m \cdot x+n
\)
1.8 Equació punt-pendent
Es dedueix de la definició de la recta amb un punt i un pendent:
\(
(y-y_0)=m \cdot (x-x_0)
\)
1.9 Equació canònica
Els denominadores de l’equació canònica són les coordenades \(x\) i \(y\) del punts de tall amb els eixos de coordenades \((a,0)\) i \((0,b)\):
\(
Ax+By+C=0\\
\frac{A}{-C}x+\frac{B}{-C}y+\frac{C}{-C}=0\\
\frac{x}{\frac{-C}{A}}+\frac{y}{\frac{-C}{B}}=1\\
a=\frac{-C}{A|}, \, b=\frac{-C}{B}\\
\frac{x}{a}+\frac{y}{b}=1
\)
Exemple:
\(
P (2,3), \, Q=(-4,6)\\[0.5cm]
Calculem \enspace el \enspace vector \enspace director\\
\vec{PQ}=(-4,6)-(2,3)=(-6,3) \enspace \\[0.5cm]
Equació \enspace vectorial)\\
(x,y)=(2,3)+t\cdot (-6,3) \\[0.5cm]
Equació \enspace paramètrica\\
x=2-6t\\
y=3+3t \\[0.5cm]
Equació \enspace contínua\\
t=\frac{x-2}{-6}=\frac{y-3}{3} \\[0.5cm]
Equació \enspace implícita \enspace o \enspace general\\
3(x-2)=-6(y-3)\\
3x-6+6y-18=0\\
3x+6y-24=0 \\[0.5cm]
Equació \enspace explícita\\
y=-\frac{3}{6}x+\frac{24}{6}\\
y=-\frac{1}{2}x+6 \\[0.5cm]
Equació \enspace canònica\\
\frac{x}{\frac{24}{3}}+\frac{y}{\frac{24}{6}}=1\\
\frac{x}{8}+\frac{y}{4}=1\\[0.5cm]
Equació \enspace punt-pendent\\
(y-2)=-\frac{1}{2}(x-3)
\)
2. Posició relativa de dues rectes
O bé dues rectes són paral·leles, o bé són secants. Per a determinar si dues rectes son paral·leles o coincidents (paral·lelisme) o secants (amb un angle qualsevol o perpendiculars) resoldrem el sistema d’equacions lineals.
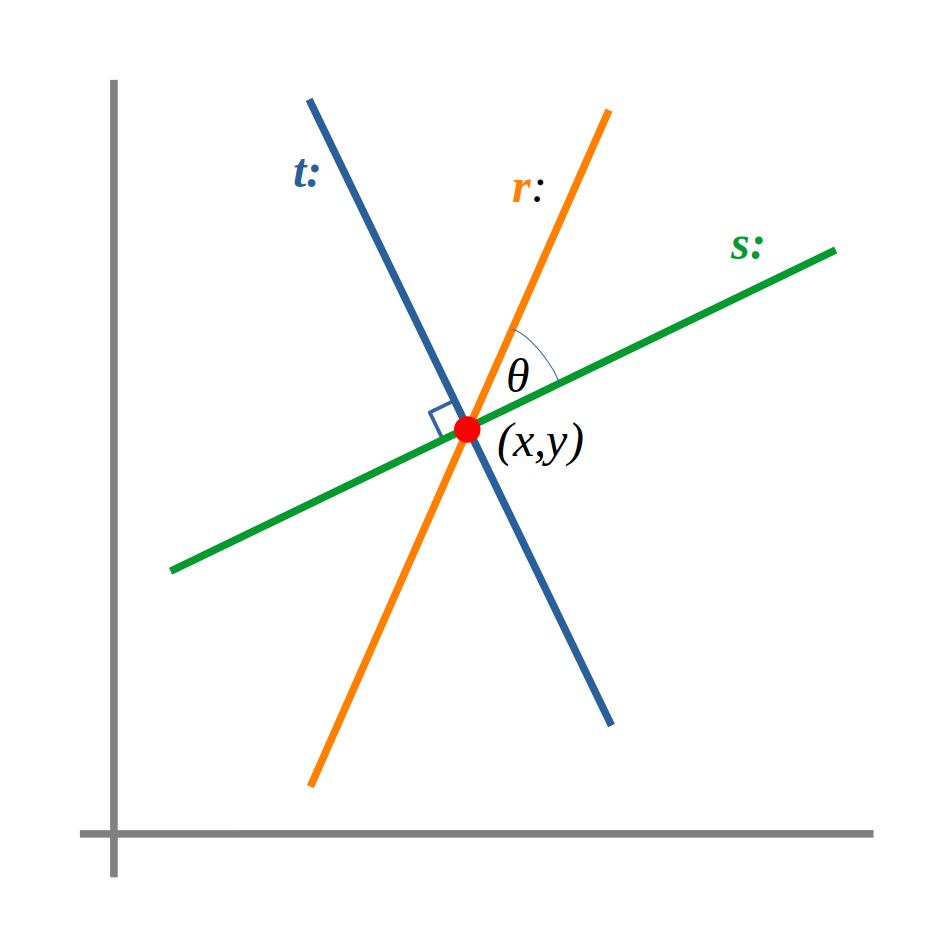 rectes perpendiculars (t:, s:) o secants amb un angle diferent de 90º (r:,s:).
rectes perpendiculars (t:, s:) o secants amb un angle diferent de 90º (r:,s:).
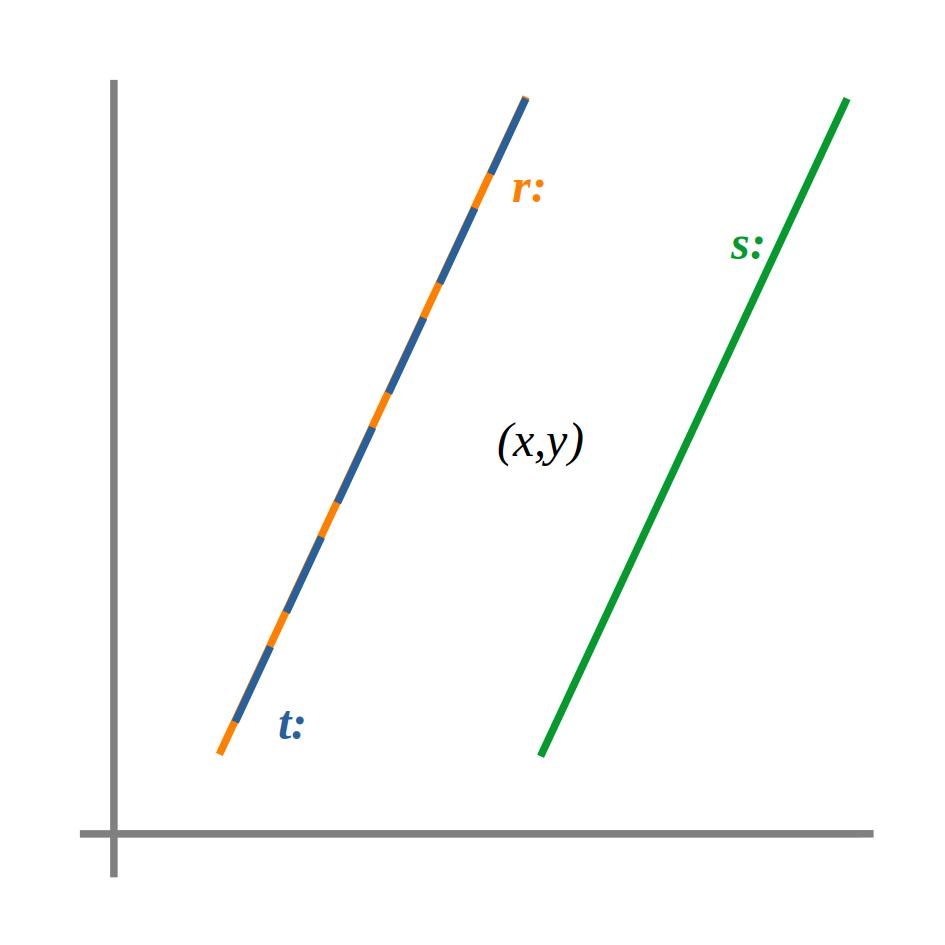 Rectes parale·les (r:, s:) o coincidents (r:, t:)
Rectes parale·les (r:, s:) o coincidents (r:, t:)
(Vegeu Classificació dels sistemes d’equacions per a saber-ne més.)
3. Distàncies i angles
Calcularem la distància mínima o perpendicular entre un punt i una recta usant la fórmula següent:
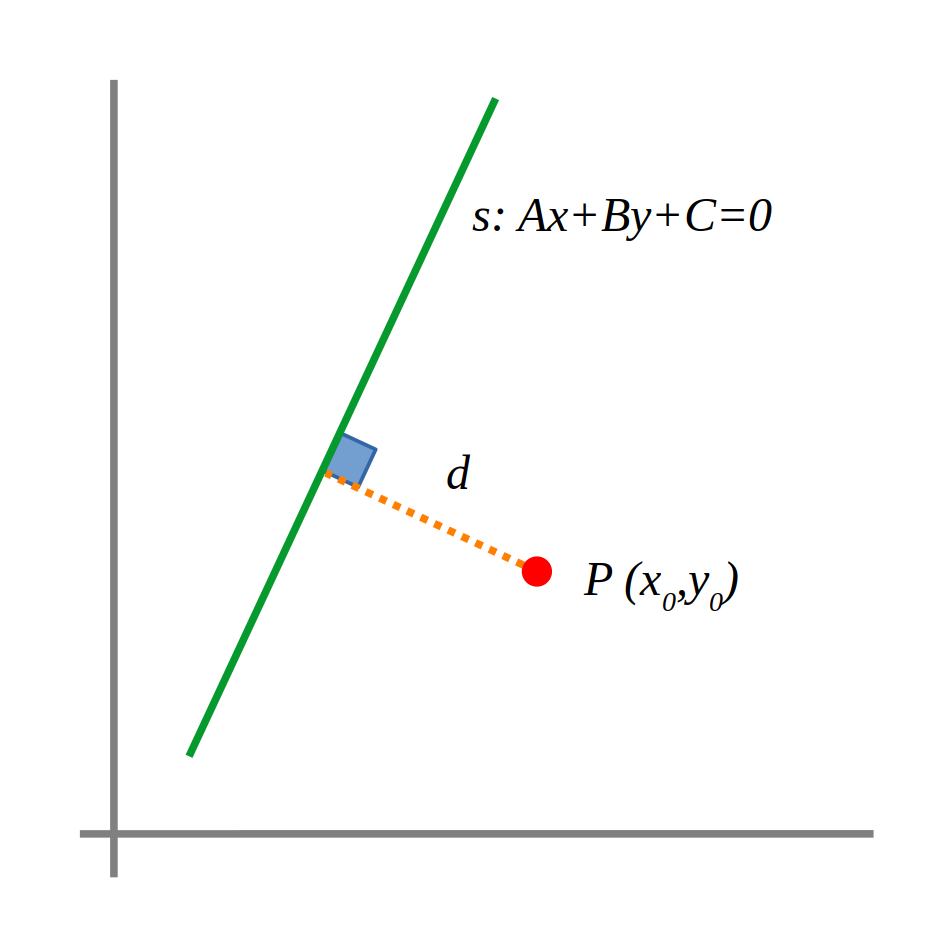
\(
d(P,r)=\frac{Ax_0+By_0+C}{\sqrt{A²+B²}}\\
\)
Exemple:
\(
P(-5,7), \enspace r:3x+6y-24=0\\
d(P,r)=\frac{3 \cdot -5+6 \cdot 7-24}{\sqrt{3²+6²}}=\frac{3}{\sqrt{45}}=\frac{1}{\sqrt{5}}u.
\)
Calcularem l’angle entre dues rectes secants amb la fórmula següent:
\(
\cos \theta=\frac{\vec u \cdot \vec v}{|u| \cdot |v|}\\
\theta=\arccos {\frac{\vec{u} \cdot \vec{v}}{|u| \cdot |v|}}
\)
Exemple:
\(
r:3x+6y-24=0, \enspace s:-5x+4y+9=0\\
\vec{n_r}=(3,6), \enspace \vec{n_s}=(-5,4)\\
\theta=\arccos \frac{(3,6) \cdot (-5,4)}{\sqrt{3²+6²} \cdot \sqrt{(-5)²+4²}}\\
\theta=\frac{-15+24}{\sqrt{45*41}}=\frac{9}{\sqrt{1845}}=\frac{9}{3\sqrt{205}}=\frac{3}{\sqrt{205}}॰
\)
Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?
Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.