1. Què és una succesió?
Una successió o progressió és un conjunt de nombres “etiquetats” amb un nombre natural que correspon a la posició de l’element.
Això vol dir que en aquest conjunt al primer element li correspon el nombre \(1\), (\(a_{1}\)), al segon element li correspon el nombre \(2\), (\(a_{2}\)), … fins a l’infinit.
Exemple:
\(a_{1} = 0, a_{2} = 1, a_{3} = 2, a_{4} = 3, a_{5} = 5, a_{6} = 8, a_{7} = 13, …\) és la successió de Fibonacci, cada terme s’obté sumant els dos anteriors.
Un altre exemple és \(a_{1} = 1, a_{2} = -1, a_{3} = 1, a_{4} = -1, a_{5} = 1, a_{6} = -1, a_{7} = 1, …\)
2. Definicions
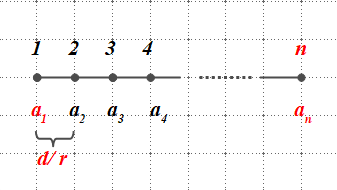
Ordre del terme de la successio \((n)\): és la posició que ocupa cada terme de la successió.
Primer terme de la successió \((a_1)\): és el primer terme de la successió.
Terme general d’una successió \((a_n)\): és el terme n-éssim (que ocupa la posició \(n\)) de la successió.
Hi ha dues maneres d’indicar el terme general d’una successió, i per tant, de definir la successió:
1.Amb la llei de recurrència: calculem \(a_{n}\) a partir d’un o més elements anteriors.
Exemple:
N’és un exemple la successió de Fibonacci: \(a_{n} = a_{n-1} + a_{n-2}=1,2,3,5,8…\)
2.Amb la llei general: per a calcular \(a_{n}\) sols ens cal saber \(n\) (el lloc que ocupa).
Exemple:
\(a_{n} = n^2 + 1: 2, 5, 10, 17,… \).
Diferència \((d)\): és la diferència que hi ha entre un terme i l’anterior d’una progressió aritmètica.
Exemple:
A la successió \(1,3,5,7,9…\) la diferència és \(2:\, 3-1=2,\, 5-3= 2,\, 7-5=2,\,9-7=2…\).
Raó \((r)\): és el quocient entre un terme i l’anterior d’una progressió geomètrica.
A la successió \(2,\, 4,\,8,\, 16,\, 32…\) la raó és \(2: \, 4 \div 2=2,\, 8 \div 4 = 2,\, 16 \div 8=2,\, 32 \div 16=2…\).
3. Progressions aritmètiques
Són successions que s’obtenen de sumar una quantitat constant (anomenada diferència, \(d\)) al terme anterior.
Hem d’indicar quin és el primer element \(a_1\), perquè aquest no té un element anterior.
Exemple:
Si \(a_{1} = 3\) i \(d = 2\), la successió és: \(3, 5, 7, 9, 11, …\).
El terme general \(a_n\) d’una progressió aritmètica es pot calcular a partir del primer element \(a_1\) i \(d\):
\(a_{2} = a_{1} + d\)
\(a_{3} = a_{2} + d = a_{1} + 2d\)
\(a_{4} = a_{3} + d = a_{1} + 3d\)
…
\(\mathbf{a_{n} = a_{n-1} + d = a_{1} + (n-1)d}\)
3.1 Suma d’una progressió aritmètica
La suma dels \(n\) termes d’una progressió aritmètica \(S_{n} = a_{1} + a_{2} + a_{3} + … + a_{n}\) és:
Si \(a_{1} = 1, d = 1,\) i \( n = 100 \Rightarrow a_n=1,2,3,…,100\) i \(S_{n} = 1 + 2 + 3 + … + 100\):
és a dir que, \(1 + 100 = 2 + 99 = 3 + 98 = … = 50 + 51 = 101\).
I per a calcular la suma sols hem de sumar \(50\) vegades \(101\).
Per tant,
\(\mathbf{S_{n} =\frac{(a_{1} + a_{n})*n}{2}}\)
4. Progressions geomètriques
S’obtenen multipicant una quantitat fixa anomenada raó, (\(r\)) per l’element anterior.
Exemple:
Si \(a_{1} = 2\) i \(d=2\), llavors \(a_n= 2, 4, 8, 16, 32,…\).
Fent la suma dels termes equidistants com abans, el terme general és:
\(\mathbf{a_{n} = a_{1}*r^{n-1}}\)
4.1 Producte d’una progressió geomètrica
Per a calcular el producte dels n primers termes \(P_{n} = a_{1}*a_{2}…*a_{n}\) d’una progressió geomètrica farem com abans el càlcul dels productes dels termes equidistants de la successió:
Exemple:
Si \(a_n=1,2,4,8,16,32…\) i volem calcular \(P_{6} = \,1*2*4*8*16*32\):
fent el producte dels termes equidistants de la successió:
\(1*…32 = 2*16 = 4*8\).
És a dir que: \(P_{6}=(a_1*a_6)^{6/2}=\sqrt{(a_1*a_6)^6}\)
Per tant, la fórmula general és:
\(\mathbf{P_{n} = (a_{1}*a_{n})^{n/2} = \sqrt{(a_{1}a_{n})^{n}}}\).
4.2 Suma d’una progressió geomètrica
Volem calcular \(S_{n} = a_{1} + a_{2} + a_{3} + … + a_{n}\) dels termes d’una progressió geomètrica.
La fórmula que ens permet fer aquest càlcul és: \(\mathbf{S_{n} = a_{1}\frac{r^n – 1}{r – 1}}\)
Exemple:
Si \(a_{1} = 2, r = 2\) i \(n = 5 \Rightarrow a_n= 2,4,8,16,32\), i per tant:
\(S_{5} = 2\frac{2^5-1}{2-1} = 2*31 = 62\).
Ho podem comprovar fent la suma manualment:
\(S_{5} = 2 + 4 + 8 + 16 + 32 = 62\).
4.2.1 De termes infinits
Si fem el límit de \(S_{n} = a_{1}\frac{r^n – 1}{r – 1}\) quan \(n \rightarrow \infty\) , és a dir, sumem els infinits termes d’una progressió geomètrica:
\(\lim_{n\to\infty} S_{n} = \lim_{n\to\infty}a_{1}\frac{r^n – 1}{r – 1} = \lim_{n\to\infty}a_{1}\frac{1 – r^n}{1 – r} = \lim_{n\to\infty}(\frac{a_{1}}{1- r} – \frac{a_{1}*r^n}{1 – r})\):
Si \(|r| > 1, r^n\) creixerà quan creixi \(n\) i \(S_n \rightarrow \infty\).
Si \(-1<|r|< 1, r^n\) anirà decreixent fins arribar a \(0\). En aquest cas, podem per tant eliminar el segon terme i:
\(\mathbf{S_n = \frac{a_{1}}{1 – r}}\).
Exemple:
Si \(a_{1}=2\) i \(r = 1/2\), llavors \(a-n=2, 1, 1/2, 1/4, 1/8,…\).
I el resultat de la suma és: \(S_n = \frac{2}{1 – 1/2} = \frac{2}{1/2} = 4\).
Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?
Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.