1. Límit d’una funció en un punt
El límit d’una funció \(f(x)\) en un punt \(x=a\) és el valor al qual s’aproxima la funció quan \(x\) s’aproxima al valor \(a: \, \lim_{x \to a} f(x)= \, L\).
Exemple:
\(y=\lim_{x \to 2}2*x+6=2*2+6=10\)
| x | y=2*x+6 |
|---|
| 1.9 | 9.8 |
| 1.99 | 9.98 |
| 1.9999 | 9.9998 |
| 1.99999 | 9.99998 |
| 1.999999 | 9.999998 |
Quan \(L\) és un valor real o infinit (\(\pm \infty\)) diem que el límit és determinat.
Exemple:
\(
\lim_{x \to 3} x^3-5= \,22 \\
\lim_{x \to \infty} x^3-5= \, \infty
\)
El límit d’una funció és indeterminat quan és un valor indefinit.
Exemple:
\(\lim_{x \to 5}\frac{x-5}{x^2-25}= \, \frac{0}{0}\).
\( \frac{0}{0}\) es un resultat indeterminat perquè té moltes solucions.
Les indeterminacions (resultat indeterminats) que podem trobar quan resolem el límit d’una funció en un punt són: \(\frac{0}{0}, \, \frac{\infty}{\infty}, \, \infty-\infty, \, 1^{\infty}, \, 0*\infty, \, 0^0 \, i \, \infty^0\).
1.1 Límits laterals d’una funció
Per a determinar quin és el límit d’una funció en un punt hem de determinar el límit d’aquesta funció quan ens hi aproximem per l’esquerra o per la dreta. Si el límits laterals no coincideixen, el límit serà indefinit i per tant la funció no tindrà límit.
Exemple:
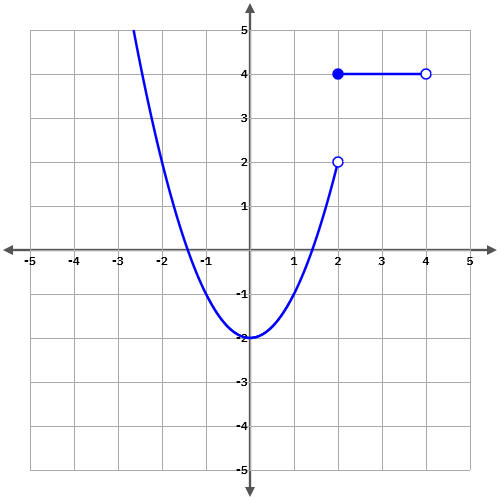
\(
f(x)
\begin{cases}
x^2-2 \enspace si \enspace-\infty \lt x \lt 2\\
4 \hspace{1.3cm} si \enspace 2 \leq x \lt 4
\end{cases}
\\[1cm]
\lim_{x \to +2^-} f(x)=\lim_{x \to +2^-}x^2-2=2\\
\lim_{x \to +2^+} f(x)=\lim_{x \to +2^+}4=4
\)
La funció anterior és una funció a trossos formada per les funcions \(y=x^2-2\) i la funció \(y=4\). Quan ens aproximem a \(x=2, \, f(x)\) té valors diferents. Els límits laterals no coindeixen, per tant, la funciò no té un límit definit.
2. Propietats dels límits
Si el límit d’una funció existeix, es compleixen les següents propietats:
i) El límit d’una suma de funcions és igual a la suma dels límits de cada funció:
\(\lim_{x \to a}[f(x)+g(x)]=\lim_{x \to \infty}f(x)+\lim_{x \to \infty}g(x)\)
ii) El límit d’un producte de funcions és igual al límit d’una funció multiplicat pel límit de l’altra:
\(\lim_{x \to a}[{f(x)}*{g(x)}]=\lim_{x \to a}f(x)*\lim_{x \to a}g(x)\)
iii) El límit d’un quocient de funcions és igual al límit de la funció dividend dividit pel límit de la funció divisor:
\(\lim_{x \to a}[\frac{f(x)}{g(x)}]=\frac{\lim_{x \to a}f(x)}{\lim_{x \to a}g(x)}\)
iv) El límit d’una funció base elevada a una funció exponent és igual al límit de la funció base elevat al límit de la funció exponent:
\(\lim_{x \to a}[{f(x}^{g(x)}]={\lim_{x \to a}f(x)}^{\lim_{x \to a}g(x)}\)
v) El límit del logaritme d’una funció és igual al logaritme del límit de la funció:
\(\lim_{x \to a}{log_a{f(x)}}=log_a[{\lim_{x \to a}f(x)}]\)
2. Càlcul de límits indeterminats
Segons el tipus d’indeterminació que resulti resolent el límit d’una funció, farem servir un mètode diferent per a determinar-ne el valor:
2.1 \((\frac{0}{0})\)
Per a resoldre aquesta indeteminació factoritzarem el numerador i el denominador, simplificarem la fracció algebraica i tornarem a fer el límit:
Exemple:
\(
\lim_{x \to 5}\frac{x-5}{x^2-25}= \, \frac{0}{0} \\
\lim_{x \to 5}\frac{x-5}{(x+5)*(x-5)}= \\
\lim_{x \to 5}\frac{1}{(x+5)}=\frac{1}{10}
\)
2.2 \((\frac{\infty}{\infty})\)
Per a resoldre aquesta indeterminació, dividim cada monomi del numerador i del denominador pel monomi de grau més gran de la funció:
\(
lim_{x \to \infty}\frac{5x^2-3x+8}{x+2}= \, \frac{\infty}{\infty} \\
lim_{x \to \infty}\frac{(5x^2-3x+8) \div x^2}{(x+2) \div x^2}= \\
lim_{x \to \infty}\frac{5x^2/x^2-3x/x^2+8/x^2}{(x/x^2+2 \div x^2)}= \\
lim_{x \to \infty}\frac{5-3/x+8/x^2}{(1/x+2/ x^2))}= \\
\frac{5+0+0}{(0+0)}= \\
\frac{5}{(0)}=\infty
\)
Però la manera més fàcil de resoldre les indeterminacions \(\frac{0}{0}, \, \frac{\infty}{\infty}\) és pel mètode de l’Hôpital. Aquest métode consisteix en derivar el numerador i el denominador fins obtenir un limit determinat:
\(
lim_{x \to 5}\frac{x-5}{x^2-25}= \, \frac{0}{0} \\
lim_{x \to 5}
\frac
{\frac{d}{dx}(x-5)}
{\frac{d}{dx}(x^2-5)}= \\
lim_{x \to 5}(\frac{1}{2x})=\frac{1}{10}
\\[1cm]
lim_{x \to \infty}(\frac{5x^2-3x+8}{x+2})= \, \frac{\infty}{\infty} \\
lim_{x \to \infty}
\frac
{
\frac{d}{dx}5x^2-3x+8
}
{
\frac{d}{dx}x+2
}= \\
lim_{x \to \infty}[\frac{10x-3}{1})]= {\infty}
\)
2.3 \((\infty-\infty)\)
Quan no podem concloure quín és el límit de la funció si la indeterminació és \(\infty-\infty\), resoldrem el límit multiplicant pel conjugat si apareixen arrels a la funció o resolent la suma/ resta de les fraccions algebraiques:
\(
\lim_{x \to \infty}{\sqrt{(6x^2+8x)}-(x+4)}= \, \infty-\infty \\
\lim_{x \to \infty}{\sqrt{6x^2+8x}-(x+4)}\frac{\sqrt{6x^2+8x}+(x+4)}{\sqrt{6x^2+8x}+(x+4)}= \\
\lim_{x \to \infty}\frac{(6x^2+8x)-(x+4)^2}{\sqrt{6x^2+8x}+(x+4)}= \frac{\infty}{\infty}\\
\lim_{x \to \infty}\frac{(5x^2/x^2-16/x^2)}{\sqrt{\frac{(6x^2+8x)}{x^4}}+(x/x^2+4/x^2))}= \\
\lim_{x \to \infty}\frac{(5)}{0}= \infty
\)
\(
\lim_{x \to 3}\frac{1}{x^2-2}-\frac{4x}{x+5}=\frac{\infty}{\infty}\\
\lim_{x \to 3}\frac{x+5-4x(x^2-2)}{(x+5)(x^2+2)}\\
\lim_{x \to 3}\frac{-4x^3+9x+5}{x^3+5x^2+2x+10}=-4
\)
2.4 \((1^{\infty})\)
El mètode més senzill per a resoldre aquesta indeterminació és: \(\lim_{x \to \infty}{f(x)}^{g(x)}=e^{\lim_{x \to \infty}{[f(x)-1]}*g(x)}\)
Exemple:
\(
\lim_{x \to \infty}{(\frac{x^2+5x}{x^3}+2)}^\frac{1}{x+1}=\\
e^{\lim_{x \to \infty}}[{(\frac{x^2+5x+2x^3}{x^3}-1)}^\frac{1}{x+1}]=\\
e^{\lim_{x \to \infty}}{(\frac{x^3+x^2+5x}{x^3})}^{\frac{1}{x+1}}=\\
e^{1}=e
\)
2.5 \((0*\infty)\)
Per a resoldre aquesta indeterminació, primer la transformarem en una altra del tipus \(\frac{0}{0}\), o bé del tipus \(\frac{\infty}{\infty}\) i després resoldrem aquesta indeterminació per l’Hôpital:
Exemple:
\(
lim_{x \to 0}[\sin x*{\frac{1}{x^2}}]\\
lim_{x \to 0}[\frac{1}{\frac{1}{\sin x}}*{\frac{1}{x^2}}]=\\
lim_{x \to 0}[\frac{1}{\frac{x^2}{\sin x}}]=\\
lim_{x \to 0}[\frac{\sin x}{x^2}]=\frac{0}{0}\\
lim_{x \to 0}[\frac{\cos x}{2x}]=\\
\frac{1}{0}=\infty
\)
2.5 \((0^0)\)
Quan tenim una funció elevada a una altra funció, usarem logaritmes per a resoldre el la indeterminació:
\(
lim_{x \to 0}{({x+5})}^{x+1}=0^0\\
lim_{x \to 0}[\ln (x+5)^{x+1}]=\\
lim_{x \to 0}[(x+1)*\ln (x+5)]=\\
lim_{x \to 0}(x+1)*lim_{x \to 0}[\ln (x+5)]=\\
1*\ln{5}=ln{5}\\
lim_{x \to 0}{({x+5})}^{x+1}=e^{\ ln 5}=5
\)
2.6 \(( \infty^0)\)
Com en el cas anterior:
\(
lim_{x \to \infty}[\ln (x+5)^{\frac{1}{x}}]=\\
lim_{x \to \infty}[(\frac{1}{x})\ln (x+5)]=0*\infty\\
lim_{x \to \infty}(\frac{1}{x})*\frac{1}{\frac{1}{\ln (x+5)}}=\\
lim_{x \to \infty}(\frac{\ln (x+5)}{x})=\frac{\infty}{\infty}\\
lim_{x \to \infty}[\frac{d}{dx} {(\frac{\ln (x+5)}{x})}]=\\
lim_{x \to \infty}\frac{\frac{1}{(x+5)}}{1}=\\
lim_{x \to \infty}\frac{1}{(x+5)}=0
\)
3. Continuïtat d’una funció
Una funció \(f(x)\) és continua en un punt si \(f(x_o)=\lim_{x \to x_o} {f(x)}\). Per tant, la funció ha de tenir limit i els límits laterals de la funció han de coincidir.
Exemple:
\(
f(x)
\begin{cases}
e^x \enspace si\enspace -\infty\leq x \lt -2 \\
x^2 \enspace si\enspace -2 \leq x \leq 2 \\
\end{cases}
\\[1cm]
i)\, x^2=4
\\
ii) \, \lim_{x \to -2}{e^x}\,=e^{-2}\\
\lim_{x \to -2}{x^2}\,=(-2)^2=4
\)
En l’exemple anterior, la funció té imatge en el punt on hi pot haver una possible disconitnuïtat \(x=-2\), però els límits laterals no coincideixen. Per tant, la funció és discontinua.
Un altre exemple:
\(
f(x)
\begin{cases}
4x+6 \enspace si\enspace -\infty\leq x \leq -5 \\
\frac{x^2+3}{-2} \enspace si\enspace -5 \lt x \lt 5 \\
\end{cases}
\\[1cm]
i. \, 4*(-5)+6=-14
\\
ii. \, \lim_{x \to -5}{4x+6}\,=-14\\
\lim_{x \to -5}\frac{x^2+3}{-2}\,=\frac{(-5)^2+3}{-2}=-14
\)
En aquest exemple, la funció també té imatge en el punt frontera entre les dues funcions \(x=-5\) i els límits laterals coincideixen. Per tant, la funció és continua.
i) Teorema de Bolzano
Si una funció \(f(x)\) és continua en un interval tancat \([a,b]\) i \(f(a)\) i \(f(b)\) són de signes diferents, existeix almenys un punt \(c \in (a,b)\) tal que \(f(c)=0\).
Exemple:
Volem saber si la funció \(f(x)=x^2-2\) té almenys una arrel en l’interval tancat \([1,2]\).
Com que és una funció polinómica, és continua en tot \(\mathbb{R}\).
\(
f(x)=x^2-2\\
f(1)=1^2-2=-1\\
f(2)=2^2-2=2\\
signf(1) \neq signf(2)
\)
Aixó vol dir que la funció SÍ té almenys una solució en aquest interval.
ii) Teorema dels valors intermedis
Si una funció \(f(x)\) és continua en un interval tancat \([a,b]\) i \(y_0\) és un valor comprès entre \(f(a), f(b)\), \(f(x)\) té el valor \(y_0\) almenys una vegada en aquest interval.
Aquest teorema és una conseqüència del teorema de Bozano: que \(f(x)=x^2-2\) sigui \(0.25\) en l’interval tancat \([1,2]\), és el mateix que dir que la funció s’anul·la en el punt \(x=1.5\) d’aquest interval , per exemple:
\(
f(x)=x^2-2-0.25=0
f(1.5)=(1.5)^2-2-0.25=0
\)
iii) Teorema de Weierstrass
Si una funció \(f(x)\) és continua en un interval tancat \([a,b]\), la funció tindrà com a mínim un màxim i un mínim absolut en aquest interval.
3.1 Discontinuïtats
3.1.1 Discontinuïtat de 1a. espècie de salt determinat
i) La funció té imatge.
ii) Els límits laterals no coincideixen i són finits.

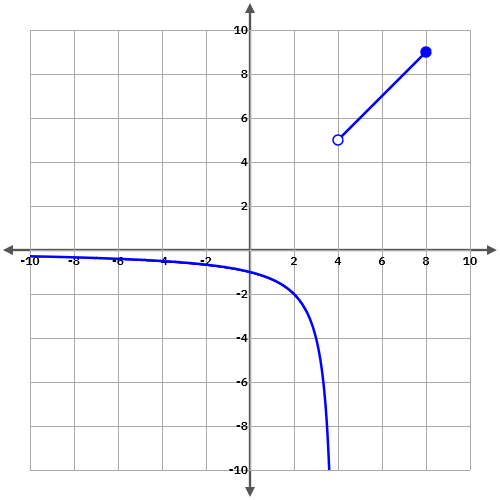
3.1.2 Discontinuïtat de 1a. espècies de salt infinit
i) La funció té imatge.
ii) Algun dels límits laterals és infinit.
3.1.3 Discontinuitat de 2a. espècie o esencial
i) La funció té imatge.
ii) Algun dels límits laterals no existeix.
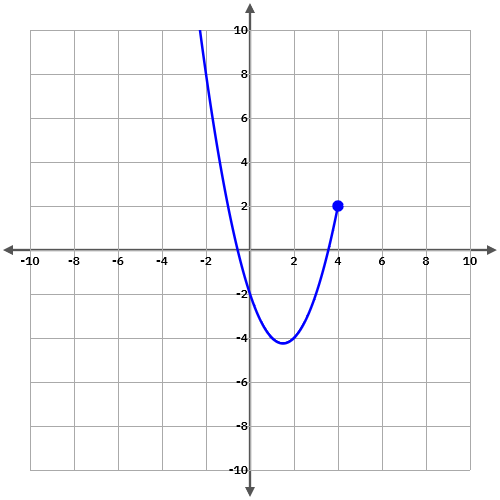
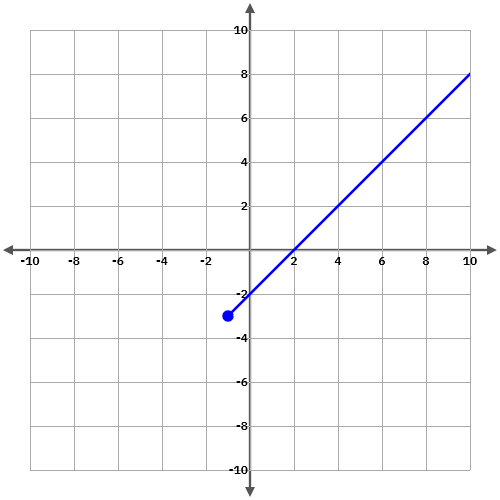
3.1.4 Discontinuïtat evitable
i) La funció no té imatge, o bé
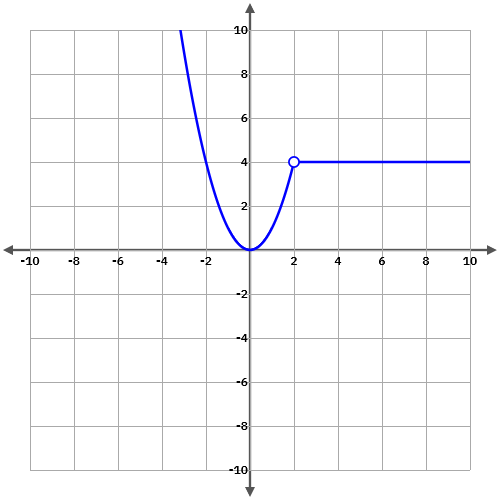
ii) la funció té imatge però no coincideix amb el límit de la funció.
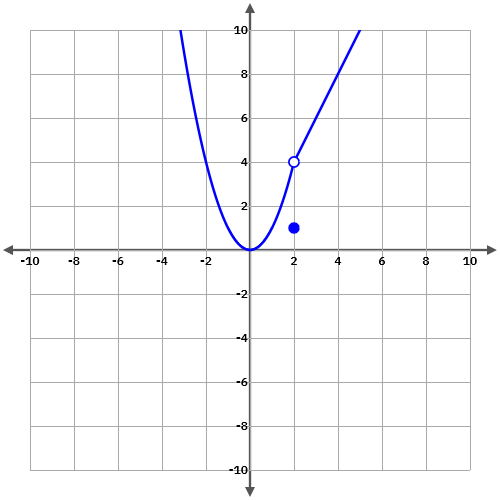
Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?
Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.