1.2 Funció elemental
Una funció elemental és una funció formada per funcions simples d’una variable amb operacions aritmètiques.
Les funcions elementals més simples són les irracionals (arrels), potències, exponencials, logarítmiques, polinòmiques, trigonomètriques i les trigonomètriques inverses. Simplificant, podem dir que són les funcions habituals que coneixem.
Exemple:
\(
y= 4 \\
y= x^3 \\
y= ln x \\
y= e^x \\
y= \sqrt {x} \\
y= x^2-9x+3 \\
y= \frac{x^2+2x+3}{x^2+1} \\
y= sin x \\
y= arcsin x \\
y= \frac{xe^x-\log_2(1+x^2)}{\sqrt{\arctan(3x)}}
\)
No hi ha una definició de funció no elemental però, per exclusió, diem que una funció no és elemental si no és una funció elemental. Una funció amb factorials, per exemple, no sería una funció elemental.
1.3 Funció composta
Una funció composta és una operació de dues funcions \(f(x), \, g(x)\) que genera una nova funció \(h(x)\): \(h(x)=f(x)∘g(x)=f[g(x)]\).
La funció \(h(x)\) és la funció resultant d’aplicar la funció \(g(x)\) a la funció \(f(x)\).
Exemple:
\(
f(x)=sin (x^3+1), \, g(x)=log (x+1) \\
h(x)=f(x)∘g(x)=f[g(x)]=
sin[log^3(x+1)+1]
\)
2. Operacions amb funcions
Si la funció suma, diferència, producte i quocient pertany alhora al domini de les funcións \(f(x), \, g(x)\), es compleix que:
\(
(f+g)(x)=f(x)+g(x) \\
(f-g)(x)=f(x)-g(x) \\
(f*g)(x)=f(x)*g(x) \\
(f \div g)(x)=f(x) \div g(x), \enspace g(x) \neq 0
\)
3. Funcions elementals
3.1 Funcions lineals
Una funció lineal \(y=m*x+n\) és una funció polinòmica de grau u, o bé zero. La gràfica de les funcions lineals és una recta. (\(a_1x+a_2x^{n-1}+a_3x^{n-2}…a_nx⁰, n \in \mathbb{R}\))
La \(m\) és el pendent o la inclinació de la recta. Si és positiva, la recta serà creixent, si és negativa serà decreixent i si és zero serà horitzontal.
La \(n\) és l’ordenada a l’origen (punt de tall amb l’eix de les \(y\) quan la \(x=0\)). L’ordenada a l’origen és el desplaçament vertical de la funció. Si és un valor positiu, estarà desplaçada cap amunt i si és negatiu cap avall.
Exemple:
\(y=2x+3, \, y= -3x, \, y=4\)
3.1.1 Propietats
El domini de la funció són tots el nombres reals (\(\mathbb{R}\).
La funció, o bé sempre creix, o bé sempre decreix o té un valor constant.
No tenen ni màxims, ni mínims, ni punts d’inflexió.
No tenen asímptotes.
No tenen ni simetria parella ni senars.
No són funcions periòdiques.
3.2 Funció proporcional
Una funció \(y=m*x+n\) és proporcional quan \(n=0\).
Exemples:
\(y=2x, \, y=-3x\)
La variació dels valors de la variable dependent \(y\) són proporcionals a la variació de la variable independent \(x\). És per això que diem que és una funció lineal proporcional.
Les funcions lineals proporcionals sempre passen per l’origen de coordenades \((0,0)\).
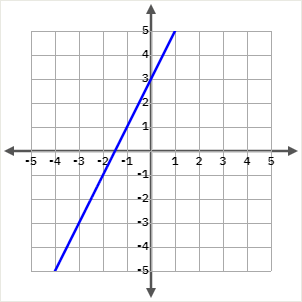
3.1.2 Funció afí
En una funció lineal afí \(n \neq 0\). Per tant, no passa per l’eix de coordenades. El valor de \(n\) indica el desplaçament vertical de la funció respecte a la funció proporcional del mateix pendent.
Exemples:
\(y=2x+3, \, y=-5x-8, \, y=6x-2 \)
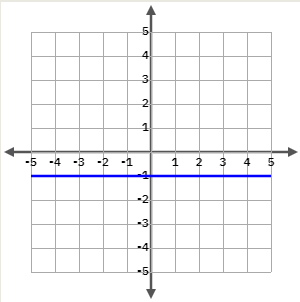
3.1.3 Funció constant
En una funció lineal constant \(m=0\) i \(n \neq 0\). Són funcions lineals de pendent zero.
Exemple:
\(y=-1\)
3.2 Funció recíproca
Les funcions recíproques \(y=\frac{\pm k}{x}\) són hipèrboles.
Exemple:
\(y=\frac{1}{x}, \, \frac{-2}{x}, \, \frac{5}{x}\)
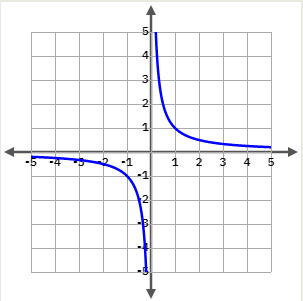
y=1/x
| x | y |
|---|
| 1000 | 0.001 |
| 100 | 0.01 |
| 10 | 0.1 |
| 0.01 | 100 |
| 0.001 | 1 000 |
| 0.000001 | 1000 000 |
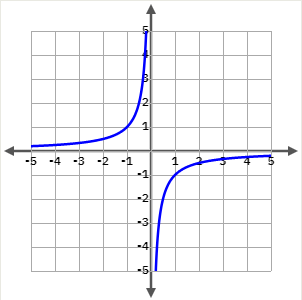
y= -1/x
| x | y |
|---|
| 1 000 | -0.001 |
| 100 | -0.001 |
| 10 | -0.1 |
| 0.01 | -100 |
| 0.0001 | -1000 |
| 0.000001 | -1 000 000 |
3.2.1 Propietats:
El domini de la funció són tots el nombres reals (\(\mathbb{R}\) ) excepte el zero.
La funció sempre creix en una branca i decreix en l’altra.
No tenen ni màxims, ni mínims, ni punts d’inflexió.
Tenen asímptotes verticals i horitzontals.
Tenen simetria senars.
No són funcions periòdiques.
3.3 Funció quadràtica
És una funció polinòmica de la forma: \(ax²+bx+c=0\).
Les funcions de segon grau són paràboles. Si el coeficient \(a\) és positiu, té forma de U i si és negatiu té forma de U invertida.
Exemple:
\(3x²-5x-7=0\)
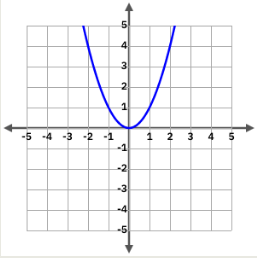
y=x²
| x | y |
|---|
| 0 | 0 |
| \(\pm 1\) | 1 |
| \(\pm 2\) | 4 |
| \(\pm 3\) | 9 |
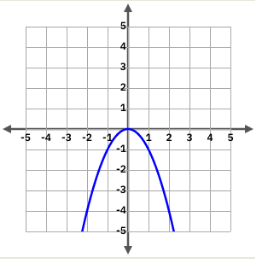
y=-x²
| x | y |
|---|
| 0 | 0 |
| \(\pm 1\) | -1 |
| \(\pm 2\) | -4 |
| \(\pm 3\) | -9 |
3.3.1 Propietats
El domini de la funció són tots el nombres reals (\(\mathbb{R}\) ).
La funció sempre creix en una branca i decreix en l’altra.
Tenen un màxim o un mínims. No tenen punts d’inflexió.
No tenen asímptotes.
Tenen simetria parella.
No són funcions periòdiques.
3. Funció racional
Són funcions de la forma \(\frac{N(x)}{D(x)}\).
Exemple:
\(\frac{x+1}{x-3}\)
El domini de la funció són tots el nombres reals excepte els que fan zero el denominador.
No són funcions periòdiques.
3.5 Funció exponencial
Són funcions de la forma \(y=a^x\) (\(a\) és una constant).
Si la \(a\) és un nombre fraccionari, la funció rotarà 180º sobre l’eix de les \(x\). Passen pel punt \((0,1)\).
Exemples:
\(y=2^x, \, y=(-3)^x, \, ({\frac{1}{2}^)x}\)
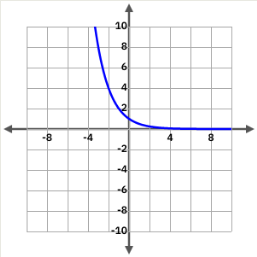
\(y=\frac{1}{2}^x\)
| x | y |
|---|
| 0 | 1 |
| 1 | \(\frac{1}{2}\) |
| 2 | \(\frac{1}{4}\) |
| 3 | \(\frac{1}{8}\) |
El domini de la funció són tots el nombres reals (\(\mathbb{R}\) ).
La funció, o bé sempre creix, o bé sempre decreix.
No tenen ni màxims ni mínims. No tenen punts d’inflexió.
Tenen una asímptota horitzontal en \(x=0\).
No tenen simetria.
No són funcions periòdiques.
3.6 Funció logarítmica
La funció logarítmica \(y=log_b(n)\) és la funció inversa de la funció exponencial \((y=a^x)\)
\((a>=0)\).
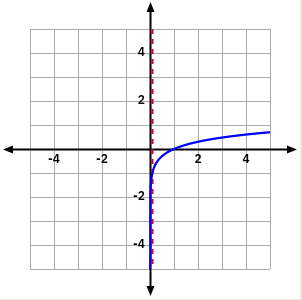
3.6.1 Propietats
El domini d’una funció logarítmica és de zero a \(+\infty\). El recorregut és tot \(\mathbb{R}\). Sempre passen pel punt \((0,1).\)
És una funció creixent.
No té ni màxims, ni mínims ni punts d’inflexió.
Té una asímptota vertical en \(x=0\).
No tenen simetria
No són funcions periòdiques.
3.7 Funcions trigonomètriques
3.7.1 Funció sinus
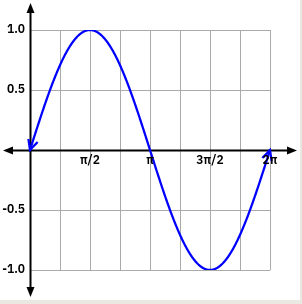
\(y=sin (x)\)
3.7.1.1 Propietats
El domini és tot \(\mathbb{R}\) (l’angle pot ser qualsevol valor). El recorregut és de \(-1 \leq x \leq+1\).
És creixent en el primer i quart quadrant i decreixent en el segon i tercer quadrant.
Té màxims a \(x=\frac {\pi}{2}+T\) i mínims a \(x=\frac {3\pi}{2}+T\).
Té punts d’inflexió a \(x=\pi+T\).
No té asímptotes.
Té simetria senar.
És periòdica \((T=2\pi).\)
3.7.2 Funció cosinus
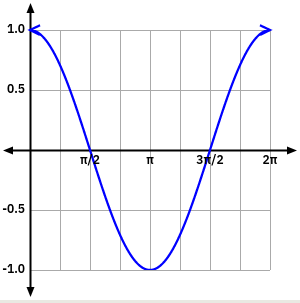
\(y=cos x\)
3.7.2.1 Propietats
El domini és tot \(\mathbb{R}\) (l’angle pot ser qualsevol valor). El recorregut és de \(-1\leq x \leq+1\).
És creixent en el tercer i quart quadrant i decreixent en el segon i tercer quadrant.
Té màxims a \(x=0+T\) i mínims a \(x=\pi+T\).
Té punts d’inflexió a \(x=\pi+T\).
No té asímptotes.
Té simetria parella.
És periòdica \((T=2\pi).\)
3.7.3 Funció tangent
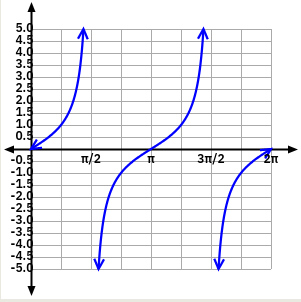
\(y=tan x\)
3.7.3.1 Propietats
El domini és tot \(\mathbb{R}\) excepte \(\frac{\pi}{2}+T\). El recorregut és de \(-\infty\leq x \leq+\infty\).
És sempre creixent.
No té màxims ni mínims.
Té punts d’inflexió a a \(x=\pi+T\).
Té asímptotes verticals a \(\frac{\pi}{2}+T\).
Té simetria parella.
És periòdica \(T=\pi\).
Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?
Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.