1. Definició
La geometria (del grec, “mesura de la Terra) és la parts de les matemàtiques que estudia les relacions entre els elements que la formen (punt, recta, pla, angles i figures) i la manera de calcular-les.
Els elements de la geometria analítica a l’espai són el punt, la recta i el pla i els angles.
2. Vectors a l’espai
Vegeu Vectors en el pla per a saber-ne més.
2.1 Producte vectorial
El producte vectorial de dos vectors és un altre vector perpendicular al pla que formen aquests dos vectors. El sentit del vector del producte vectorial es pot determinar amb la regla de la mà dreta.
El mòdul del vector resultant del producte vectorial de dos vectors representa l’àrea tancada per aquests vectors.
El producte vectorial no és commutatiu.
Per a calcular el producte vectorial de dos vectors farem el següent determinant:
\(
\vec u_1=x_1 \cdot \vec i + y_1 \cdot \vec j + z_1 \cdot \vec k\\
\vec u_2=x_2 \cdot \vec i + y_2 \cdot \vec j + z_2 \cdot \vec k\\
\vec u_1 \times \vec u_2=\begin{vmatrix} i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix}=\\
\vec i(y_1z_2-y_2z_1) – \vec j(x_1z_2-x_2z_1) + \vec k(x_1y_2-x_2y_1)
\)
Exemple:
\(
\vec {u_1}=(-5,3,1)\\
\vec {u_2}=(1,2,-4)\\
\vec {u_1} \times \vec {u_2}=\begin{vmatrix} i & j & k \\ -5 & 3 & 1 \\ 1 & 2 & -4 \end{vmatrix}=\\
\vec i(3 \cdot-4-2 \cdot 1) -\vec j(-5 \cdot -4-1 \cdot 1) + \vec k(-5 \cdot 2-1 \cdot 3)\\
\vec {u_3}=\vec i(-14) – \vec j(19) + \vec k(-13)\\
A=|\vec {u_3}|=\sqrt{(-14)² +(-19)² + (-13)²}=26.94 \; u²\\
\)
2.2 Producte mixt
El producte mixt de tres vectors \([u,v,w]\) s’obté multiplicant escalarment el primer vector pel producte vectorial del segon i el tercer. També es pot calcular fent el determinat dels tres vectors. Representa el volum tancat per aquests tres vectors.
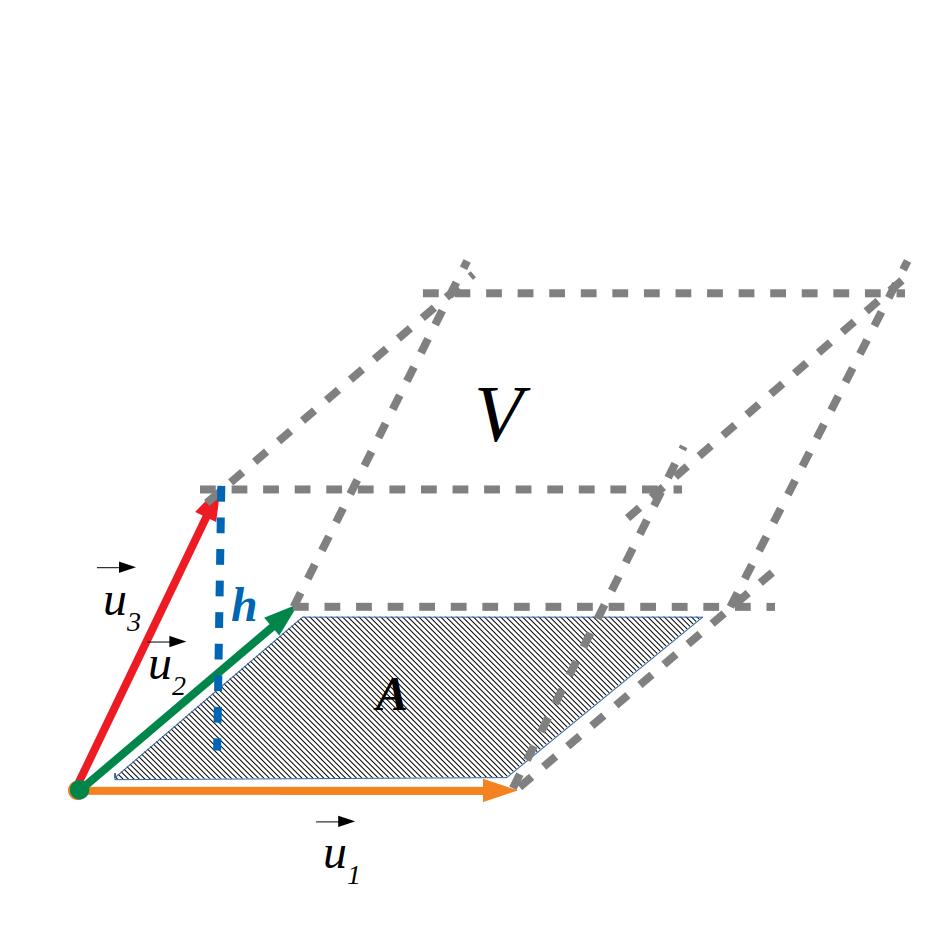
\(
\vec u_1=x_1 \cdot \vec i + y_1 \cdot \vec j + z_1 \cdot \vec k\\
\vec u_2=x_2 \cdot \vec i + y_2 \cdot \vec j + z_2 \cdot \vec k\\
\vec u_3=x_3 \cdot \vec i + y_3 \cdot \vec j + z_3 \cdot \vec k\\
\vec u_1 \cdot (\vec u_2 \times \vec u_3)=\begin{vmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{vmatrix}
\)
Exemple:
\(
\vec u_1=2 \cdot \vec i + 3 \cdot \vec j + 1 \cdot \vec k\\
\vec u_2=-5 \cdot \vec i + 3 \cdot \vec j + 1 \cdot \vec k\\
\vec u_3=1 \cdot \vec i + 2 \cdot \vec j + 4 \cdot \vec k\\
V=\begin{vmatrix} 2 & 3 & 1 \\ -5 & 3 & 1 \\ 1 & 2 & 4 \end{vmatrix}=70 \; u³
\)
3. Equació de la recta
\(
(x,y,z)=(x_0,y_0,z_0)+t(u_1,u_2,u_3)\\
x=x_0+ t \cdot u_1\\
y=y_0+ t \cdot u_2\\
z=z_0+ t \cdot u_3\\
t=\frac{x-x_0}{u_1}=\frac{y-y_0}{u_2}=\frac{z-z_0}{u_3}\\[0.5cm]
u_2(x-x_0)=u_1(y-y_0)\\
u_3(y-y_0)=u_2(z-z_0)\\[0.5cm]
u_2x-u_2x_0-u_1y+u_1y_0=0\\
u_3y-u_3y_0-u_2z+u_2z_0=0\\[0.5cm]
u_2x-u_1y+(-u_2x_0+u_1y_0)=0\\
u_3y-u_2z+(-u_3y_0+u_2z_0)=0\\[0.5cm]
\begin{cases}
\pi_1: A_1x+B_1y+C_1z+D_1=0\\
\pi_2:A_2x+B_2y+C_2z+D_2=0
\end{cases}
\)
(Vegeu Equacions de la recta de Geometria en el pla per a saber-ne més).
4. Equació del pla
Per a definir tots els punts d’un pla ens calen tres punts o dos vectors i un punt.
Si \(O\) és l’origen de coordenades del sistema de referència, \(\vec u_1, \vec u_2\) són els dos vectors del pla de referència, \(P\) és un punt del pla de referència i \(X\) és el punt que volem definir, l’equació vectorial del pla amb dos vectors i un punt és: \(\vec {OX}=\vec{OP}+\vec{PX}\).
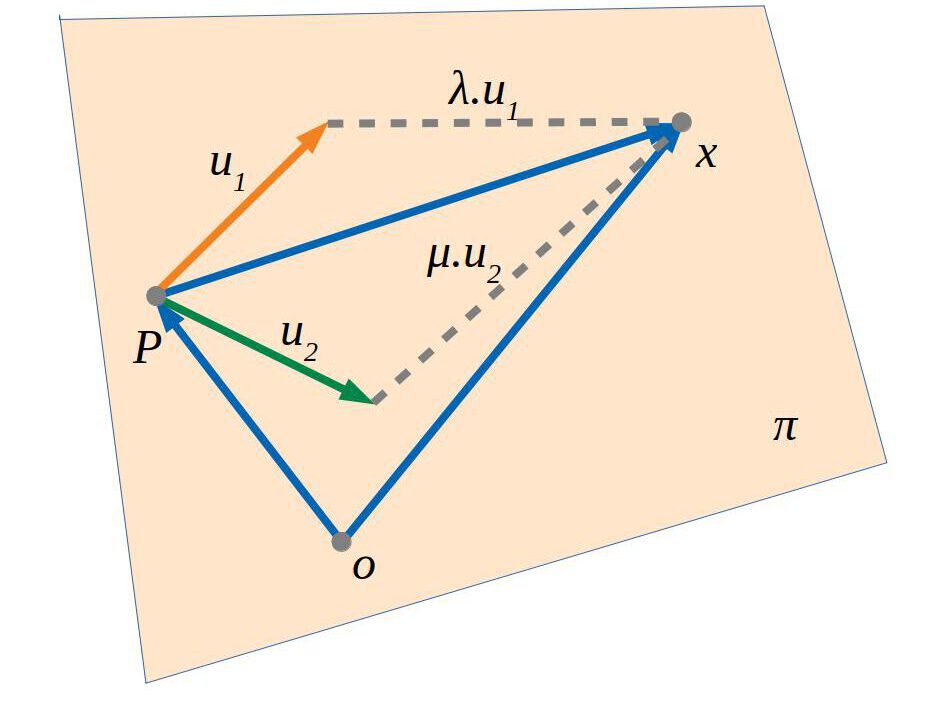
\(
(x,y,z)=(x_0,y_0,z_0)+t(u_1,u_2,u_3)+s(v_1,v_2,v_3)\\
x-x_0=t \cdot u_1+ s \cdot v_1\\
y-y_0=t \cdot u_2+ s \cdot v_2\\
z-z_0=t \cdot u_3+ s \cdot v_3\\[1cm]
\pi: \begin{vmatrix} x-x_0 & y-y_0 & z-z_0 \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix}=0\\[1cm]
(x-x_0) \cdot \begin{vmatrix} u_2 & u_3 \\ v_2 & v_3 \end{vmatrix}
–
(y-y_0) \cdot \begin{vmatrix} u_1 & u_3 \\ v_1 & v_3 \end{vmatrix}
+
(z-z_0) \cdot \begin{vmatrix} u_1 & u_2 \\ v_1 & v_2 \end{vmatrix}\\
(x-x_0)(u_2v_3-v_2u_3)-(y-y_0)(u_1v_3-v_1u_3)+(z-z_0)(u_1v_2-v_1u_2)\\
x(u_2v_3-v_2u_3)-y(u_1v_3-v_1u_3)+z(u_1v_2-v_1u_2)+\\
-x_0(u_2v_3-v_2u_3)+y_0(u_1v_3-v_1u_3)-z_0(u_1v_2-v_1u_2)=0\\[1cm]
\pi:Ax+By+Cz+D=0
\)
El vector \((A,B,C)\) de l’equació general és el vector normal de pla (vector lliure perpendicular a una recta, pla, o a un corba qualsevol):
\(\vec n(A,B,C)\)
Exemple:
\(
(x,y,z)=(2,3,1)+t(-5,3,1)+s(1,2,4)\\
x-2=-5t+1s\\
y-3=3t+2s\\
z-1=1t+4s\\[0.5cm]
(x-2) \cdot \begin{vmatrix} 3 & 1 \\ 2 & 4 \end{vmatrix}
(y-3) \cdot \begin{vmatrix} -5 & 1 \\ 1 & 4 \end{vmatrix}
+
(z-1) \cdot \begin{vmatrix} -5 & 3 \\ 1 & 2 \end{vmatrix}=0\\
(x-2) \cdot 10-(y-3) \cdot -21+(z-1) \cdot -13=0\\[0.5cm]
\pi:10x+21y-13z+36=0
\)
Si tenim tres punts, \(A,B,C\), calcularem dos vectors (\(\vec{AB}, \vec{AC}\), per exemple) i l’equació general del pla serà :
\(
\begin{vmatrix} x-x_0 & y-y_0 & z-z_0 \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix}=0
\)
4.1 Feix de plans
Definim un feix de plans a partir de dos plans que formen la recta d’intersecció comuna de tot els plans del feix (aresta del feix):
\(
r:
\begin{cases}
A_1x+B_1y+C_1z+D_1=0 \\
A_2x+B_2y+C_2z+D_2=0 \\
\end{cases}
\\[1cm]
\alpha(A_1x+B_1y+C_1z+D_1)+\beta(A_2x+B_2y+C_2z+D_2)=0
\)
És a dir que, l’equació del feix de plans és la combinació lineal dels dos plans que determinen la recta \(r\).
Si \(\alpha\) és zero, tenim l’equació del segon pla, i si \(\beta\) és zero tenim la del primer pla.
També es pot definir l’equació del feix com:
\(
\frac{\alpha} {\alpha}(A_1x+B_1y+C_1z+D_1)+\frac {\beta} {\alpha} (A_2x+B_2y+C_2z+D_2)=0\\
(A_1x+B_1y+C_1z+D_1)+\gamma (A_2x+B_2y+C_2z+D_2)=0
\)
Exemple:
\(
r:
\begin{cases}
-5x+3y+1z+3=0 \\
1x+2y+4z-2=0 \\
\end{cases}
\\[1cm]
\alpha(-5x+3y+1z+3)+\beta(1x+2y+4z-2)=0
\)
5. Posicions relatives
Podem estudiar la posició relativa de rectes i plans comparant-ne, o bé els punts i vectors, o bé comparant els rangs de les matrius formades amb les equacions generals de les rectes.
Si tenim l’equació general d’una recta però ens cal un vector i un punt, haurem de calcular-ne les equacions vectorial, paramètrica o continua.
Per a calcular l’equació paramètrica d’una recta si en tenim la general, farem:
- Assignarem a alguna de les variables, per exemple la zeta, el paràmetre \(\lambda\). Aquesta variable (o el paràmetre \(\lambda\)) serà la variable independent del sistema d’equacions indeterminat.
- Resoldrem el sistema d’equacions indeterminat per reducció eliminant la \(x\) per a obtenir la \(y\) en funció de \(z\).
- Resoldrem el sistema d’equacions indeterminat eliminant la \(y\) per a obtenir \(x\) en funció de \(z\).
També podem resoldre els passos 2 i 3 resolent el sistema d’equacions per Gauss o Crammer.
- Agruparem les equacions resultants i obtenim l’equació paramètrica de la recta. Fent les operacions habituals de l’apartat 3 podem obtenir qualsevol altre equació de la recta.
\(
\begin{cases}
\pi_1:4x-8y+5z=7\\
\pi_2:x-9y+z=6
\end{cases}\\
1. z=\lambda\\
2. y=-\frac{17}{28}-\frac{1}{28}\lambda\\
3. x=\frac{15}{28}-\frac{37}{28}\lambda\\
4. \begin{cases}
x=\frac{15}{28}-\frac{37}{28}\lambda\\
y=\frac{17}{28}-\frac{1}{28}\lambda\\
z=\lambda
\end{cases}
\)
Per a calcular l’equació general d’una recta si en tenim la paramètrica o continua farem com en l’exemple anterior els passos habituals per obtenir les diferents equacions d’una recta:
\(
\begin{cases}
x=2-3\lambda\\
y=5+5\lambda\\
z=-1-4\lambda
\end{cases}\\
\lambda=\frac{x-2}{-3}=\frac{y-5}{5}=\frac{z+1}{-4}\\
5(x-2)=-3(y-5)\\
5x+3y-25=0\\
-4(y-5)=5(z+1)\\
-4y-5z+15=0\\
r:
\begin{cases}
5x+3y-25=0\\
-4y-5z+15=0
\end{cases}
\)
Per a calcular sols el vector d’una recta si en tenim l’equació general farem el producte vectorial del vectors normals de les equacions generals dels plans:
\(
\begin{cases}
\pi_1:4x-8y+5z=7\\
\pi_2:x-9y+z=6
\end{cases}\\
\vec {n_1}=(4,-8,5), \; \vec {n_2}=(1,-9,1)\\
\vec v_r=\vec {n_1} \times {\vec n_2}\\
\begin{vmatrix}i & j & k \\ 4 & -8 & 5 \\ 1 & -9 & 1 \end{vmatrix}\\
\vec i {(-8+45)}-\vec j {(4-5)}+\vec k {(-36+8)}\\
\vec {v_r}=37 \vec i+1 \vec j -28 \vec k
\)
5.1 Recta-recta
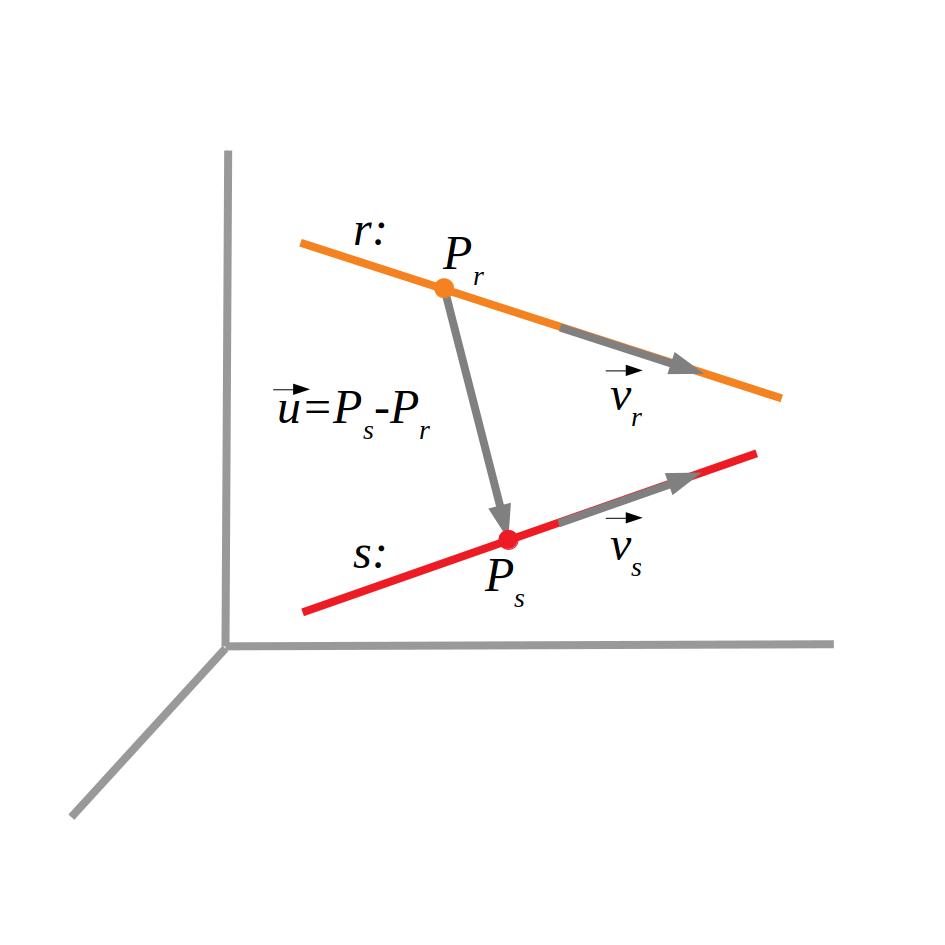
Si usem un vector \(\vec v\) i un punt de cada recta (\(P_r,P_s\)):
| Posició relativa | Comparació punts i vectors |
|---|
| Coincidents | \(\frac{\vec u_1}{\vec v_1}=\frac{\vec u_2}{\vec v_2}=\frac{\vec u_3}{\vec v_3} \; i \; P_r=P_s\) |
| Paral·leles | \(\frac{\vec u_1}{\vec v_1}=\frac{\vec u_2}{\vec v_2}=\frac{\vec u_3}{\vec v_3} \; i \; P_r \neq P_s\) |
| Secants | \(\frac{\vec u_1}{\vec v_1} \neq \frac{\vec u_2}{\vec v_2} \neq \frac{\vec u_3}{\vec v_3}\) i \(det(D)=0\) |
| S’encreuen | \(\frac{\vec u_1}{\vec v_1} \neq \frac{\vec u_2}{\vec v_2} \neq \frac{\vec u_3}{\vec v_3}\) i \(det(D) \neq 0\) |
Farem servir les equacions vectorial, paramètrica o continua per a determinar el vector i el punt de cada recta.
\(
r: (x,y,z)=(x_r,y_r,z_r)+ \lambda(v_{r1},v_{r2}, v_{r3})\\
s:(x,y,z)=(x_s,y_s,z_s)+ \lambda(v_{s1},v_{s2}, v_{s3})\\
r:\begin{cases}
x=x_r+ \lambda \cdot v_{r1}\\
y=y_r+ \lambda \cdot v_{r2}\\
z=z_r+ \lambda \cdot v_{r3}\\
\end{cases}\\[1cm]
s:\begin{cases}
x=x_s+ \mu \cdot v_{s1}\\
y=y_s+ \mu \cdot v_{s2}\\
z=z_s+ \mu \cdot v_{s3}\\
\end{cases}\\
\frac{x-x_0}{v_{r1}}=\frac{y-y_0}{v_{r2}}=\frac{z-z_0}{v_{r3}}\\
\frac{x-x_0}{v_{s1}}=\frac{y-y_0}{v_{s2}}=\frac{z-z_0}{v_{s3}}\\
\vec v_r:(v_{r1},v_{r2},v_{r3}), \; P_r(x_r,y_r,z_r)\\
\vec v_s:(v_{s1},v_{s2},v_{s3}), \; P_r(x_s,y_s,z_s)
\)
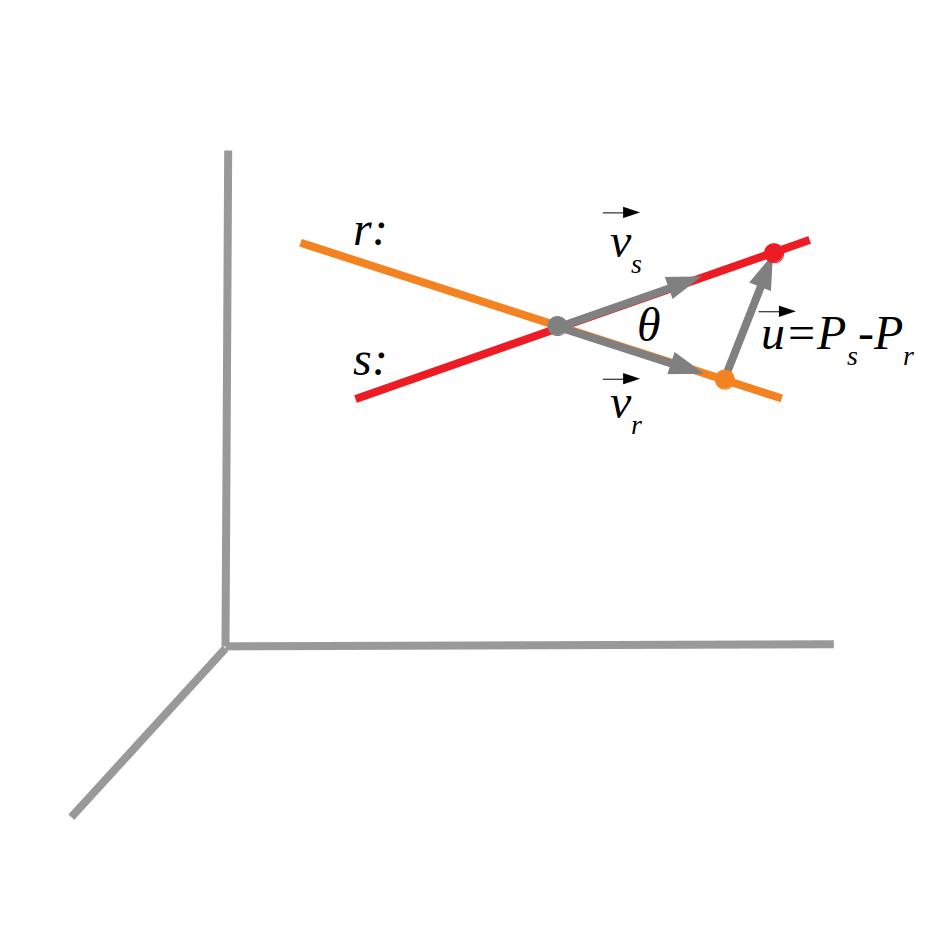
Si les rectes són coincidents, els vectors directors seran paral·lels i tindran els mateixos punts.

Si són paral·leles, els vectors directors seran paral·lels però tindran punts diferents.
Si les rectes són secants, els vectors directors no seran paral·lels i el determinant \(D\) dels dos vectors i el vector \((x_2-x_1,y_2-y_1,z_2-z_1)\) serà zero.
\(
D=\begin{vmatrix} x_2-x_1 & y_2-y_1 & z_2-z_1 \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix}=0
\)
Si les rectes s’encreuen, els vectors directors no seran paral·lels i el determinant \(D\) dels dos vectors i el vector \((x_2-x_1,y_2-y_1,z_2-z_1)\) serà diferent de zero:
\(
D=\begin{vmatrix} x_2-x_1 & y_2-y_1 & z_2-z_1 \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix} \neq 0
\)
Exemple:
\(
r: (x,y,z)=(2,3,1))+t(-5,3,1)\\
s:
\begin{cases}
x=3+1s\\
y=4+2t\\
z=5+4s
\end{cases}\\
P_r=(2,3,1), \; v_r=(-5,3,1)\\
P_s=(3,4,5), \; v_s=(1,2,4)\\
\frac{-5}{1} \neq \frac{3}{2} \neq \frac{1}{4}\\
\begin{vmatrix}3-2 & 4-3 & 5-1 \\-5 & 3 & 1 \\1 & 2 & 4 \end{vmatrix}=-21\\[1cm]
\text{Per tant, les dues rectes s’encreuen.}
\)
Per a analitzar la posició relativa comparant els rangs de les matrius de coeficients i ampliada hem d’usar les equacions generals de les dues rectes:
| Posició relativa | Rang matriu coeficients(*) | Rang matriu ampliada(*) |
|---|
| Coincidents | 3 | 4 |
| Paral·leles | 2 | 3 |
| Secants | 3 | 3 |
| S’encreuen | 3 | 4 |
\(
r:
\begin{cases}
3x+5y-21=0\\
y-3z=0
\end{cases}\\
s:
\begin{cases}
2x-y-2=0\\
4y-2z-6=0
\end{cases}\\[1cm]
\text{Matriu de coeficients (A)}=
\begin{vmatrix}
3 & 5 & 0 \\ 0 & 1 & -3 \\ 2 & -1 & 0 \\ 0 & 4 & -2
\end{vmatrix}\\
\text{Matriu ampliada (A*)}=
\begin{vmatrix}
3 & 5 & 0 & 21 \\ 0 & 1 & -3& 0\\ 2 & -1 & 0 & 2 \\ 0 & 4 & -2 & 6
\end{vmatrix}\\[1cm]
\text{Rang A}=3\\
\text{Rang A*}=4\\[1cm]
\text{Per tant, s’encreuen}
\)
5.2 Exercicis
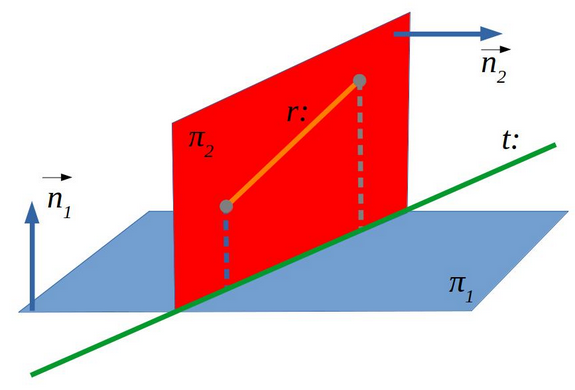
5.2.1 Projecció d’una recta sobre un pla
Per a calcular la projecció d’una recta sobre un pla, fem:
- Calculem el vector normal del pla que conté la recta (\(\pi_2\)) fent el producte vectorial del vector de la recta i el vector normal del pla de projecció (tots dos són vectors del pla que conté la recta).
- Calculem el terme independent \(D\) de \(\pi_2\) usant el punt de la recta que també és un punt d’aquest pla.
- L’equació de la recta projectada és la formada per les equacions generals dels dos plans.
\(
r:
\begin{cases}
x=1+5\lambda\\
y=-2-2\lambda\\
z=\lambda
\end{cases}
\\[1cm]
\pi_1:30x+2y-z+9=0
\\[1cm]
1.
\\
\vec n_2=\vec v_r \times \vec n_1\\
\vec n_2=(5,-2,1) \times (30,2,-1)=(0,35,70)
\\[1cm]
2.
\\
\pi_2:0x+35y+70z+D=0\\
\pi_2:0 \cdot 1+35 \cdot -2+70 \cdot 0+D=0, \; D=70\\
\\
\pi_2:35y+70z+70=0
\\[1cm]
3.
\\t:
\begin{cases}
\pi_1:30x+2y-z+9=0\\
\pi_2:35y+70z+70=0
\end{cases}
\)
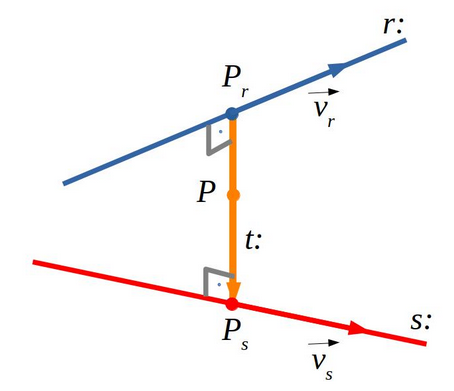
5.2.2 Recta perpendicular a dues rectes que s’encreuen
El procediment és:
- Expressem genèricament un punt de cada recta (\(P_r,P_s\)) i calculem el vector entre aquests dos punts (\(\vec {P_rP_s}\)).
- Aquest vector ha de ser perpendicular a les rectes que s’encreuen, per tant el producte escalar amb els vectors de les rectes ha de ser zero.
- Resolent el sistema d’equacions trobem el valor dels paràmetres de cada recta que fan que la recta \(t:\) sigui perpendicular i en calculem un vector perpendicular.
- Fem passar la recta perpendicular \(t:\) per un dels punts del vector \(P_r,P_s\) i tenim l’equació de la recta perpendicular a dues rectes que s’encreuen.
\(
r:
\begin{cases}
x=4+2\lambda\\
y=1-\lambda\\
z=-2+3\lambda
\end{cases}
\\[1cm]
s:
\begin{cases}
x=1+\mu\\
y=-2-2\mu\\
z=8+2\mu
\end{cases}
\\[1cm]
1.
\\
P_r:(4+2\lambda,1-\lambda,-2+3\lambda)\\
P_s:(1+\mu,-2-2\mu,8+2\mu)\\
\vec {P_rP_s}={[(4+2\lambda)-(1+\mu)],[(1-\lambda)-(-2-2\mu)],[(-2+3\lambda)-(8+2\mu)]}=\\
(3+2\lambda-\mu,3-\lambda+2\mu,-10+3\lambda-2\mu)\\[1cm]
2.
\\
\vec {P_rP_s} \cdot \vec v_r=0\\
(3+2\lambda-\mu,3-\lambda+2\mu,-10+3\lambda-2\mu) \cdot (2,-1,3)=0\\
-27+14\lambda-10\mu=0\\
\vec {P_rP_s} \cdot \vec v_s=0\\
(3+2\lambda-\mu,3-\lambda+2\mu,-10+3\lambda-2\mu) \cdot (1,-2,2)=0\\
-23+10\lambda-9\mu=0
\\[1cm]
3.
\\
\begin{cases}
-27+14\lambda-10\mu=0\\
-23+10\lambda-9\mu=0
\end{cases}\\
\lambda=\frac{1}{2}, \; \mu=-2
\\
\vec {P_rP_s}=(3+2\lambda-\mu,3-\lambda+2\mu,-10+3\lambda-2\mu)=(2,-\frac{3}{2},-\frac{13}{2})\\
\\[1cm]
4.
\\
t:
\begin{cases}
x=4+2\cdot \psi\\
y=1-\frac{3}{2} \cdot \psi\\
z=-2 -\frac{13}{2} \cdot \psi
\end{cases}
\)
5.2.3 Recta que passa per un punt que talla a dues rectes
És la recta formada per cada un dels dos plans \(\pi_1,\pi_2\) que contenen a \(r,s\) respectivament i que passa per \(P\). Per a calcular l’equació d’aquesta recta hem de trobar les equacions dels plans que contenen a \(r:, s:, \; i \; P\):
- Calculem el vector normal de \(\pi_1\) fent el producte vectorial del vector de la recta \(r:\) i el vector \(\vec {PP_r}\).
- Calculem el vector normal de \(\pi_2\) fent el producte vectorial del vector de la recta \(s:\) i el vector \(\vec {PP_s}\).
- Calculem els plans \(\pi_1,\pi_2\) amb les vectors normals i el punt \(P\).
- L’equació de la recta és la formada per les equacions generals dels dos plans.
\(
P(2,3,4)\\
r:
\begin{cases}
x=5-\lambda\\
y=-6+5\lambda\\
z=1+2\lambda
\end{cases}
\\
\vec v_r=(-1,5,2),P_r=(5,-6,1),
\\[1cm]
s:
\begin{cases}
x=1+2\lambda\\
y=-6+\lambda\\
z=3+3\lambda\\
\end{cases}
\\
\vec v_s=(2,1,3),P_s=(1,-6,3)
\\[1cm]
1.
\\\vec {PP_r}=P_r-P=(5,-6,1)-(2,3,4)=(3,-9,-3)\\
\vec n_1=(-1,5,2) \times(3,-9,-3)=(3,3,-6)\\[1cm]
2. \\
\vec {PP_s}=P_s-P=(1,-6,3)-(2,3,4)=(-1,-9,-1)\\
\vec n_2=(2,1,3) \times (-1,-9,-1)=(26,-1,-17)\\[1cm]
3.
\\
\pi_1:3x+3y–6z+D_1=3 \cdot 2+3 \cdot 3-6 \cdot 4+D_1=0,D_1=9\\
\pi_2:26x-1y-17z+D_2=26 \cdot 2-1 \cdot 3-17 \cdot 4+D_2=0,D_2=+19
\\[1cm]
4.
\\t:
\begin{cases}
\pi_1:3x+3y-6z+9=0\\
\pi_2:26x-1y-17z+19=0
\end{cases}
\)
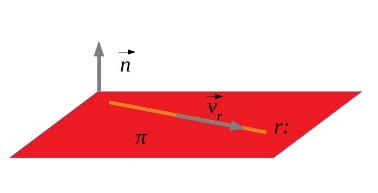
5.3 Recta-pla
Per a determinar la posició relativa d’una recta i un pla comparant punts i vectors usarem les equacions vectorial, paramètrica o continua de la recta i l’equació general del pla. Per fer-ho amb rangs, ens calen les equacions generals de la recta i del pla.
\(
r:
(x,y,z)=(x_r,y_r,z_r)+\lambda(v_{r1},v_{r2},v_{r3})\\
r:\begin{cases}
x=x_r+ \lambda \cdot v_{r1}\\
y=y_r+ \lambda \cdot v_{r2}\\
z=z_r+ \lambda \cdot v_{r3}\\
\end{cases}\\
\frac{x-x_0}{v_{r1}}=\frac{y-y_0}{v_{r2}}=\frac{z-z_0}{v_{r3}}\\
v_r(v_{r1},v_{r2},v_{r3}), \; P_r(x_r,y_r,z_r)\\[1cm]
\pi: A_1x+B_1y+C_1z+D_1=0\\
\vec n=(A,B,C)
\)
| Posició relativa | Comparació punts i vectors |
|---|
| Recta continguda en el pla | \(\vec v_r \cdot \vec n=0\; i \; P_r \in \pi\) |
| Recta i pla paral·lels | \(\vec v_r \cdot \vec n=0\; i \; P_r \notin \pi\) |
| Recta i pla secants | \(\vec v_r \cdot \vec n \neq 0\) |
| Posició relativa | Rang matriu coeficients(*) | Rang matriu ampliada(*) |
|---|
| Recta continguda en el pla | 2 | 2 |
| Recta i pla paral·lels | 2 | 3 |
| Recta i pla secants | 3 | 3 |
Si la recta està continguda en el pla, el producte escalar del vector de la recta i el normal del pla serà zero i els punts de la recta són punts del pla. Per a saber si un punt de la recta és també un punt del pla el substituirem a l’equació del pla:
Exemple:
\(
r:
\begin{cases}
x=2-5\lambda\\
y=3+3\lambda\\
z=1+\lambda
\end{cases}\\
v_r(-5,3,1), \; P_r(2,3,1)\\[1cm]
\pi:2x+4y-2z-14=0\\
\vec n(2,4,-2)\\[1cm]
\vec v_r \cdot \vec n=(-5,3,1) \cdot (2,4,-2)=-5 \cdot 2+3 \cdot 4-1 \cdot 2=-10+12-2=0\\
\pi(2,3,1)=2 \cdot 2+4 \cdot 3 -2 \cdot 1-14=4+12-2-14=0\\[1cm]
\text{El pla i la recta són paral·lels i la recta està continguda en el pla.}
\)
Si la recta i el pla són paral·lels, el producte escalar dels dos vectors serà zero, però els punts de la recta i del pla són diferents:
\(
r:
\begin{cases}
x=2-5\lambda\\
y=4+3\lambda\\
z=3+\lambda
\end{cases}
\Rightarrow r:
\begin{cases}
3x+5y-26=0\\
x+5z-17=0
\end{cases}\\
\pi:4x+6y+2z-28=0\\[1cm]
\vec v_r(-5,3,1), \; P_r(2,4,3)\\
\vec n_\pi(4,6,2)\\[1cm]
\vec v_r \cdot \vec n_\pi=(-5,3,1) \cdot (4,6,2)=-20+18+2=0 \text{ (Recta i pla són paral·lels)}\\
\pi(2,4,3):4 \cdot 2+6 \cdot 4+2 \cdot 3-28=10 \text{ (Els punts de la recta no śon del pla)}\\[1cm]
\text{Per tant, la recta i el pla són paral·lels}\\[1cm]
\text{Matriu A}=\begin{bmatrix}3 & 5 & 0 \\ 1 & 0 & 5 \\ 4 & 6 & 2 \end{bmatrix}\\
\text{Matriu A*}=\begin{bmatrix}3 & 5 & 0 & 26 \\ 1 & 0 & 5 & 17 \\ 4 & 6 & 2 & 28\end{bmatrix}\\
\text{Rang A}=2 \\
\text{Rang A*}=3 \\
\text{Per tant, la recta i el pla són paral·lels}
\)
Si el pla i la recta són secants , la recta tallarà el pla en un punt (Q). Q serà el punt que resulta de fer el sistema d’equacions generals de la recta i el pla.
\(
r:
\begin{cases}
2x-7y+8z=3\\
3x+5y-z=7
\end{cases}\\
\pi:x+3y-4z=0\\
\begin{bmatrix}2 & -7 & 8 & 3 \\ 3 & 5 & -1 & 7 \\ 1 & 3 & -4 & 0\end{bmatrix}\\
x=1 ,\; y=1 , \; z=1 \\
Q=(1,1,1)
\)
5.4 Pla-pla
Per a determinar la posició relativa de dos plans determinarem els rangs de les equacions generals del plans, o bé compararem els vectors i els punts de cada pla:
| Posició relativa | Comparació punts i vectors |
|---|
| Coincidents | \(\frac{A_1}{B_1}=\frac{A_2}{B_2}=\frac{C_1}{C_2}=\frac{D_1}{D_2}\) |
| Paral·lels | \(\frac{A_1}{B_1}=\frac{A_2}{B_2}=\frac{C_1}{C_2} \neq \frac{D_1}{D_2}\) |
| Secants | \(\frac{A_1}{B_1} \neq \frac{A_2}{B_2} \neq \frac{C_1}{C_2}\) |
| Posició relativa | Rang matriu coeficients(*) | Rang matriu ampliada(*) |
|---|
| Coincidents | 1 | 1 |
| Paral·lels | 1 | 2 |
| Secants | 2 | 2 |
\(
\pi_1: A_1x+B_1y+C_1z+D_1=0\\
\pi_2:A_2x+B_2y+C_2z+D_2=0
\)
 Plans coincidents
Plans coincidents
 Plans paral·lels
Plans paral·lels
 Plans secants
Plans secants
5.4.1 Plans bisectors
Un pla bisector és un pla que passa per l’aresta d’un angle dièdric i el divideix en dos angles iguals. Un angle dièdric és una regió de l’espai compresa entre dos semiplans que tenen la mateixa recta, anomenada aresta de l’angle dièdric.
Per a calcular els dos plans bisectors que formen l’angle dièdric, farem:
\(
d=\left| \frac{Ax_1+By_1+Cz_1+D_1}{\sqrt{A_1²+B_1²+C_1}²} \right|=\pm \frac{Ax_2+By_2+Cz_2+D_2}{\sqrt{A_2²+B_2²+C_2²}}
\)
Exemple:
\(
P(x_0,y_0,z_0)\\
\pi_1:2x+3y-4z-6=0\\
\pi_2:-3x+4y-2z=0\\[1cm]
d(P,\pi_1)=d(P,\pi_2)\\
\left| \frac{2x_0+3y_0-4z_0-6}{\sqrt{2²+3²+(-4)²}} \right|=\pm \frac{-3x_0+4y_0-2z_0-0}{\sqrt{(-3)²+4²+(-2)²}}\\
\sqrt{29} \cdot (2x_0+3y_0-4z_0-6)=\pm \sqrt{29} \cdot (-3x_0+4y_0-2z_0-0)\\
(2x_0+3y_0-4z_0-6)=+(-3x_0+4y_0-2z_0-0)\\
\sigma_1: 5x-y-2z-6=0\\
(2x_0+3y_0-4z_0-6)=-(-3x_0+4y_0-2z_0-0)\\
\sigma_2: -x+7y-6z-6=0
\)
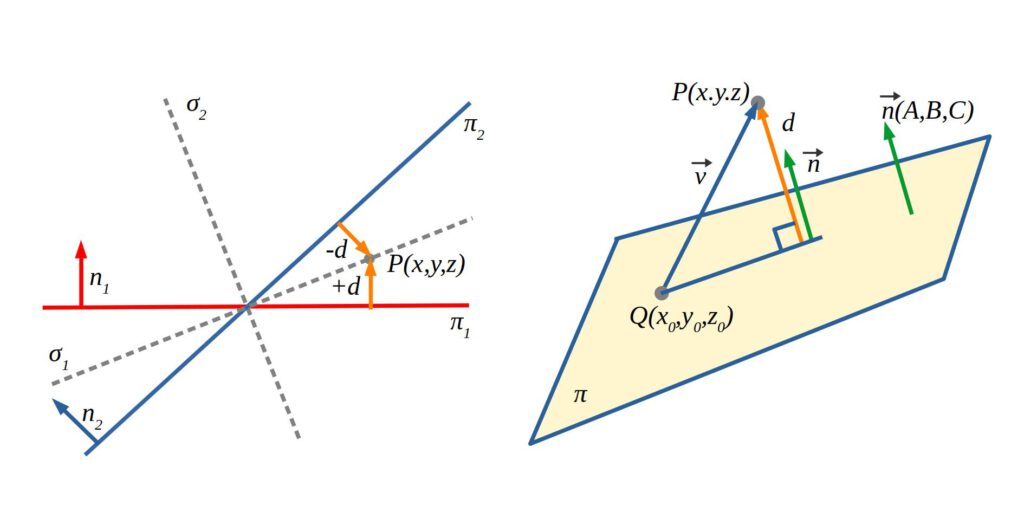
La distància \(d\) mínima o perpendicular d’un punt \(P\) a un pla (o a una recta) és el mòdul del vector projecció entre un punt del pla (origen) i el punt P (extrem).
El signe del vector distància és positiu si el sentit d’aquest vector és el mateix que el del vector normal del pla, i és negatiu si els sentits d’ambdós vectors són contraris.
5.5 Tres plans
Per a determinar la posició relativa de tres plans hem d’usar les equacions generals dels plans i calcular el rang de la matriu de coeficients i de l’ampliada. En alguns casos, també hem de tenir en compte els vectors directors dels plans per tal de no confondre dues posicions relatives amb el mateix resultat quan comparem els rangs:
\(
\pi_1: A{_1} x+B{_1} y+C{_1} z+D{_1}=0\\
\pi_2: A{_2} x+B{_2} y+C{_2} z+D{_2}_=0\\
\pi_3: A{_3} x+B{_3} y+C{_3} z+D{_3}=0
\)
| Posició relativa | Comparació vectors directores | Rang matriu coeficients(*) | Rang matriu ampliada(*) |
|---|
| Coincidents | | 1 | 1 |
| Paral·lels dos a dos | | 1 | 2 |
| Paral·lels i dos de coincidents | \(\frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}=\frac{D_1}{D_2}\) | 1 | 2 |
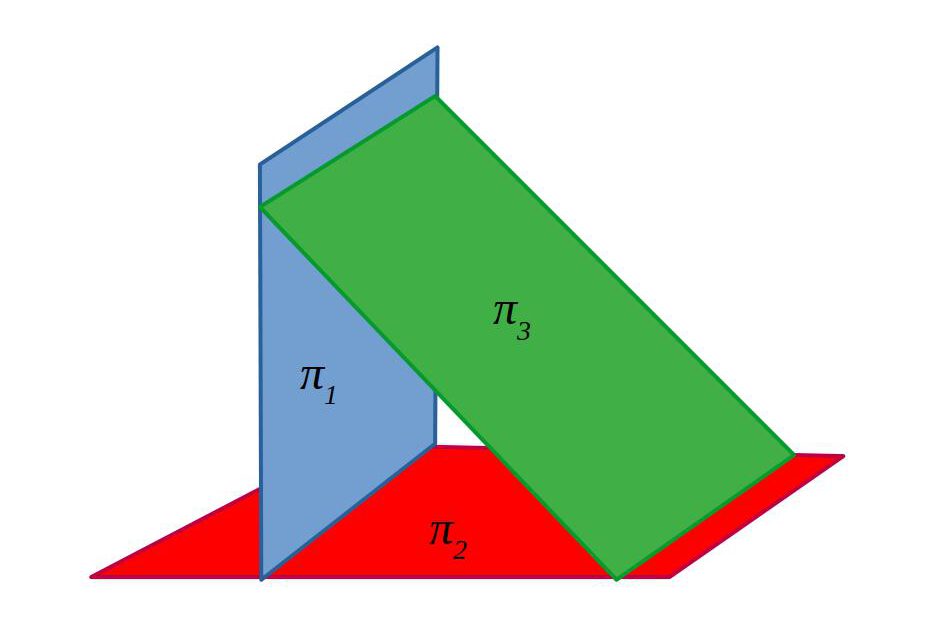
| Secants i diferents | | 2 | 2 |
| Dos de coincidents i un de secant | \(\frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}=\frac{D_1}{D_2}\) | 2 | 2 |
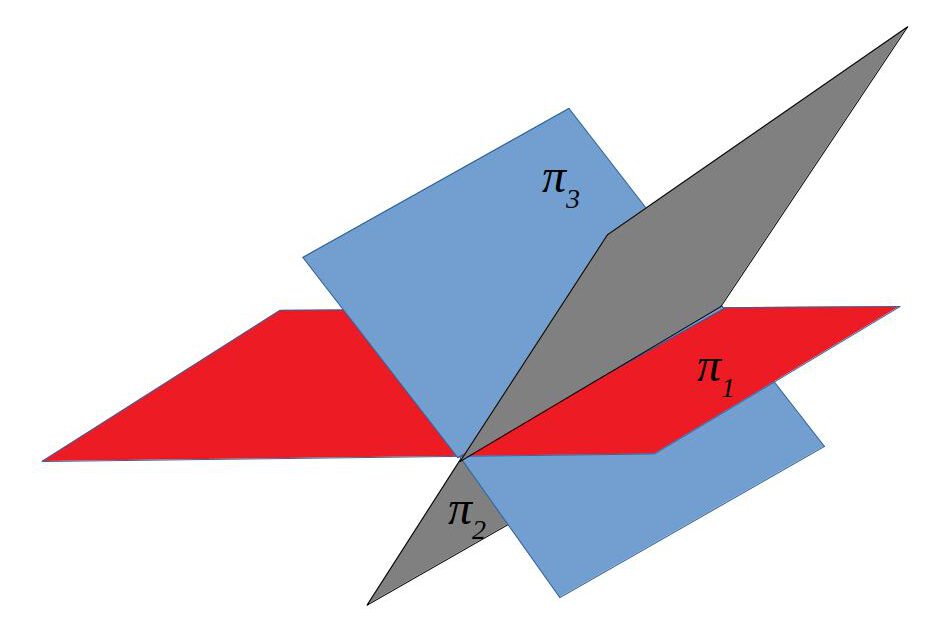
| Secants dos a dos | | 2 | 3 |
| Dos de paral·lels i un de secant | \(\frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2} \neq \frac{D_1}{D_2}\) | 2 | 3 |
| Secants en un punt | | 3 | 3 |
 Tres plan coincidents
Tres plan coincidents
 Paral·lels dos a dos
Paral·lels dos a dos
 Secants i diferents
Secants i diferents
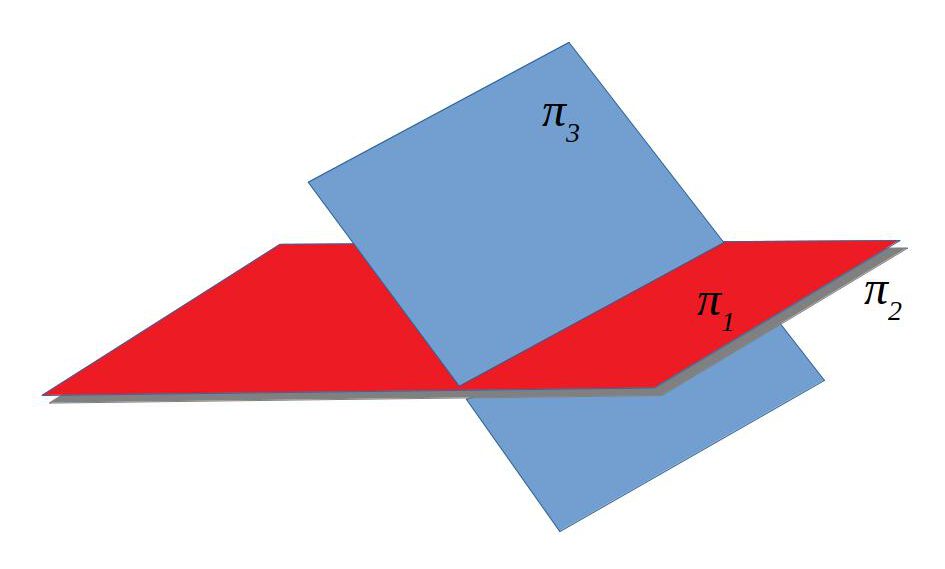 Dos de coincidents i un de secant
Dos de coincidents i un de secant
 Paral·lels i dos de coincidents
Paral·lels i dos de coincidents
 Secants dos a dos
Secants dos a dos
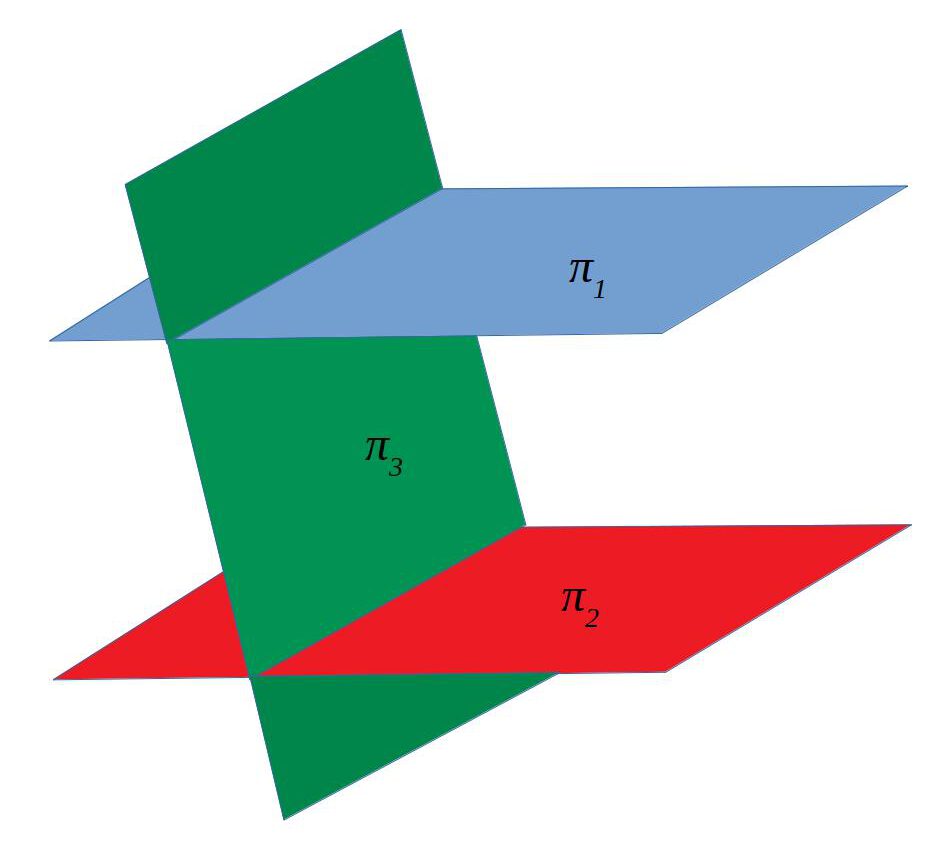 Dos de paral·lels i un de secant
Dos de paral·lels i un de secant
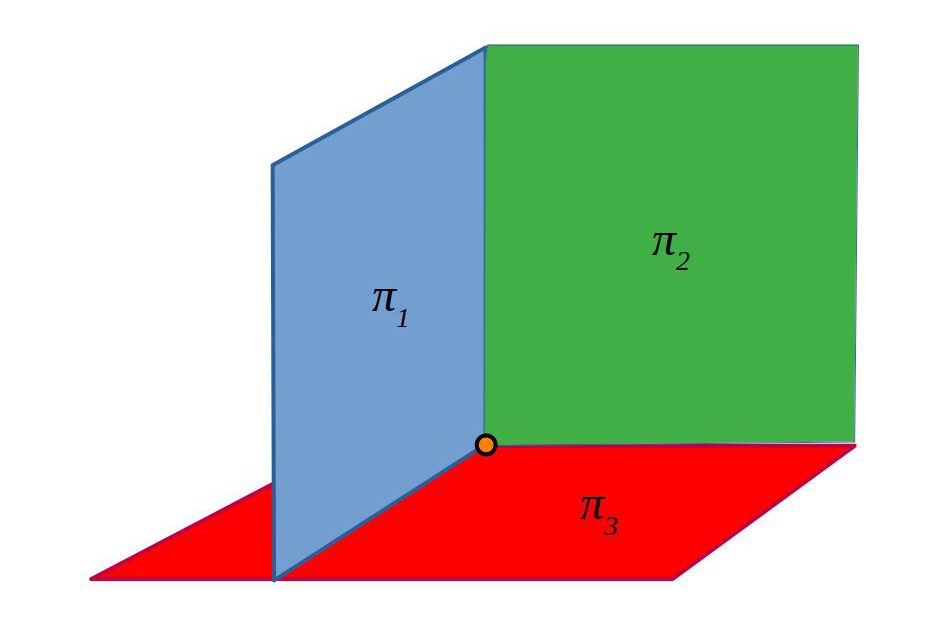 Secants en un punt
Secants en un punt
6. Distàncies i angles
6.1 Distàncies
6.1.1 Punt-recta
La distància mínima és la distància perpendicular entre el punt i la recta.
El procediment que usarem és el següent:
\(
\left| \vec v_r \right| \cdot d=\left| \vec v \times \vec v_r \right|\\
d=\frac{\left| \vec v \times \vec v_r \right|}{\left| \vec v_r \right|}\\[1cm]
\)
Exemple:
\(
P(1,2,3)\\
r:\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-5}{1}\\
\vec v_r=(2,3,1), \; P_r=(1,2,5)\\[1cm]
\vec v=P-P_r=(1,2,3)-(1,2,5)=(0,0,-2)\\
d=\frac{\left| (0,0,-2) \times (2,3,1) \right|}{\left| (2,3,1) \right|}=
\sqrt{\frac{26}{7}} \; u.
\)
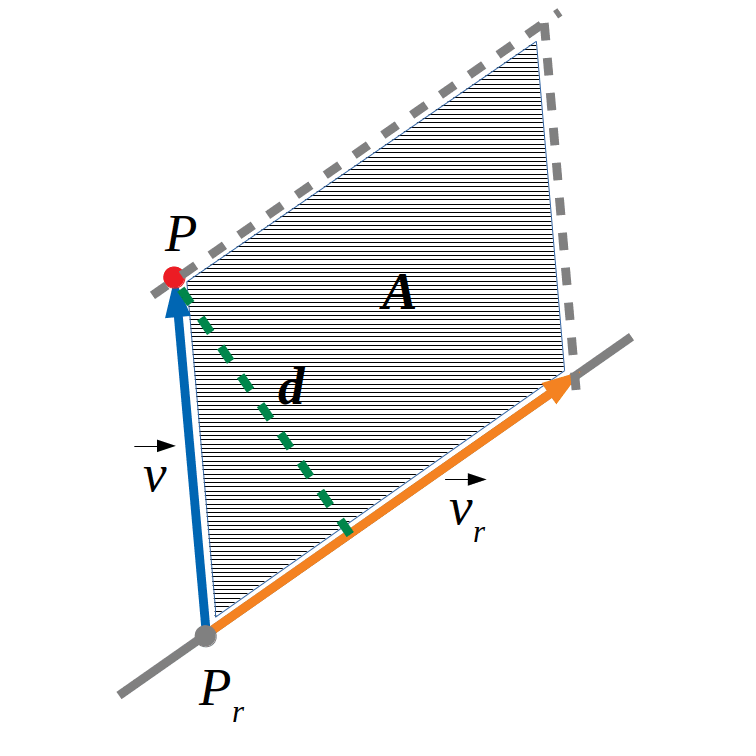
També podem calcular la distància de la següent manera (més complicada):
El vector normal \(\vec n\) del pla perpendicular a la recta és el vector de la recta \(\vec v_r\).
- l’equació del pla de vector normal \(\vec n\) que conté el punt \(P\).
- Trobem el punt d’intersecció de la recta \(Q\) i el pla resolent el sistema d’equacions formats per les equacions generals.
- Calculem el mòdul del vector \(\vec {PQ}\).
\(
P_0(1,2,3)\\
r:\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-5}{1}\\[1cm]
1.\\
\vec v_r=\vec n=(2,3,1)\\
\pi:2x+3y+z+D=0 \\[1cm]
2.\\
2 \cdot 1+3 \cdot 2 +1 \cdot 3+D=0, \; D=-11\\
\pi: 2x+3y+z-11=0\\[1cm]
3.\\
\begin{cases}
2x+3y+z=11\\
3x-2y=-1\\
1x-2z=-9
\end{cases}\\
x=\frac{5}{7}, \, y=\frac{11}{7}, \; z=\frac{34}{7}\\[1cm]
4.\\
\vec {PQ}=P-Q=(\frac{5}{7},\frac{11}{7},\frac{34}{7})-(1,2,3)=(-\frac{2}{7},-\frac{3}{7},\frac{13}{7})\\
d=\sqrt{(-\frac{2}{7})²+(-\frac{3}{7})²+(\frac{13}{7})²}=\sqrt{\frac{26}{7}} \; u.
\)
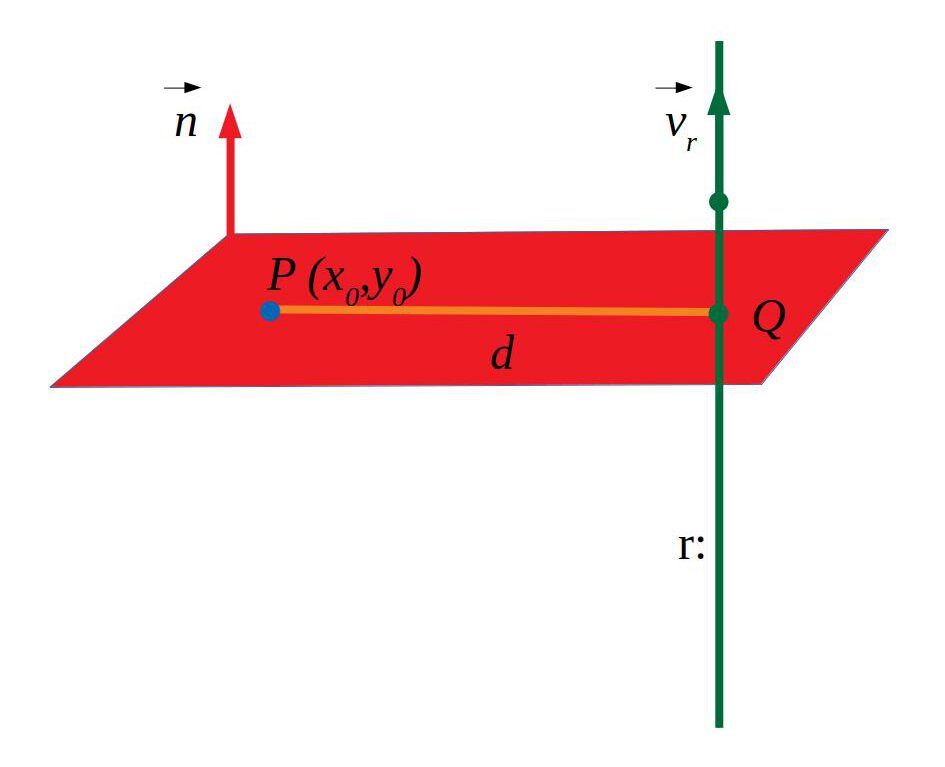
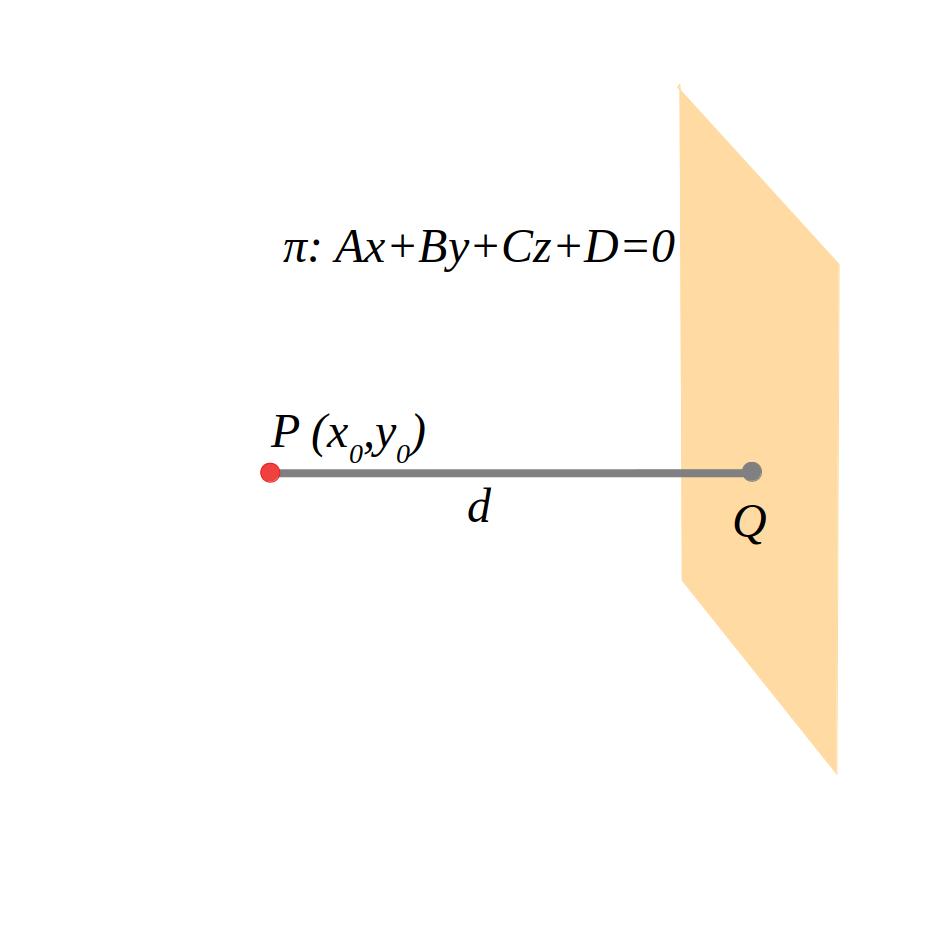
6.1.2 Punt-pla
La distància d’un punt a un pla es calcula fent \(d(P,\pi)=\frac{Ax_0+By_0+Cz_0+D}{\sqrt{A²+B²+C²}}\). L’equació del pla ha d’estar en forma general.
Exemple:
\(
P_o(3,2,1)\\
\pi:-5x+6y-4z+10=0\\
\\[0.5cm]
d(P_o,\pi)=\left|\frac{-5 \cdot 3+6 \cdot 2-4 \cdot 1+10}{\sqrt{(-5)²+(6)²+(-4)²}}\right|\approx 3.76
\)
6.1.3 Punt-punt
Per a calcular la distància entre dos punts hem de calcular el mòdul del vector entre els dos punts.
Exemple:
\(
P(3,2,1), \; Q(-4,2,2)\\
d(P,Q)=\left|\vec {PQ}\right|=\left|Q-P\right|\\
\left|(-4,2,2)-(3,2,1)\right|=\sqrt{(-7)²+(0)²+(1)²}=\sqrt {50} \; u.
\\[0.5cm]
M=\frac{P+Q}{2}=\frac{(3,2,1)+(-4,2,2)}{2}=(\frac{-1}{2},2,\frac{3}{2})
\)
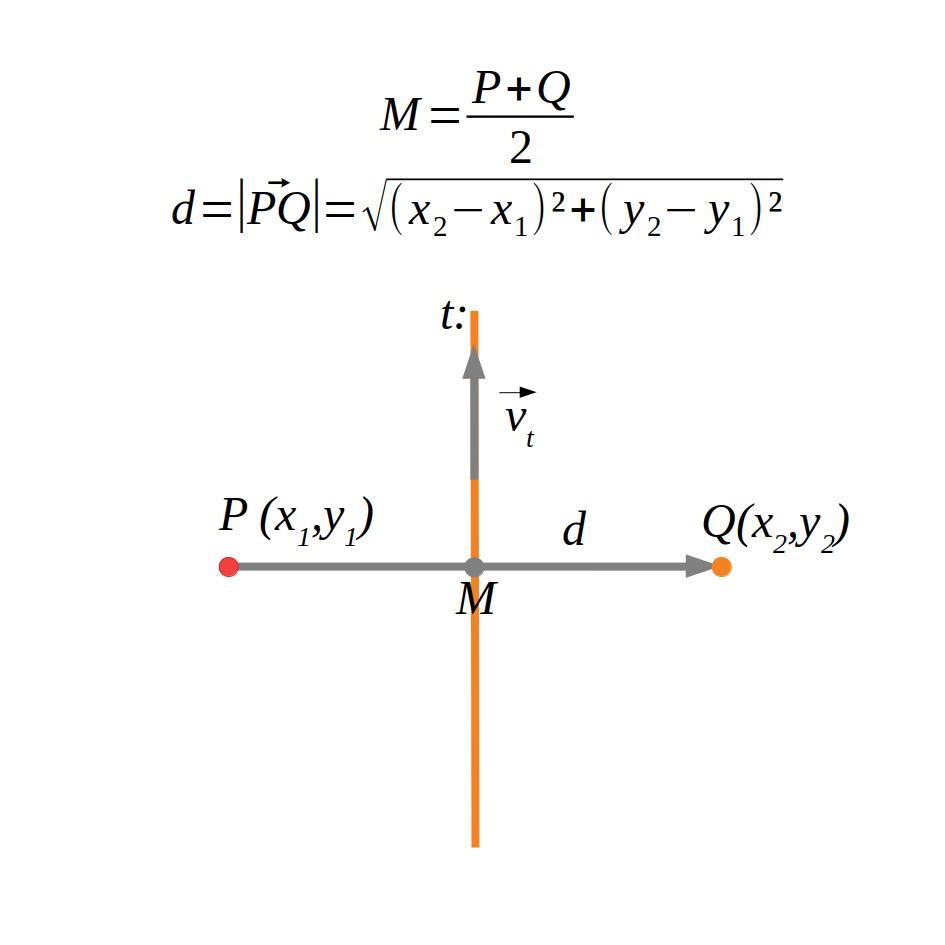
6.1.4 Recta-recta
Es determina calculant la distància d’un punt d’una recta a l’altra recta.
6.1.5 Recta-pla
Es determina calculant la distància d’un punt de la recta al pla.
6.1.6 Pla-pla
Es determina calculant la distància d’un punt d’un pla a l’altre pla.
6.2 Angles
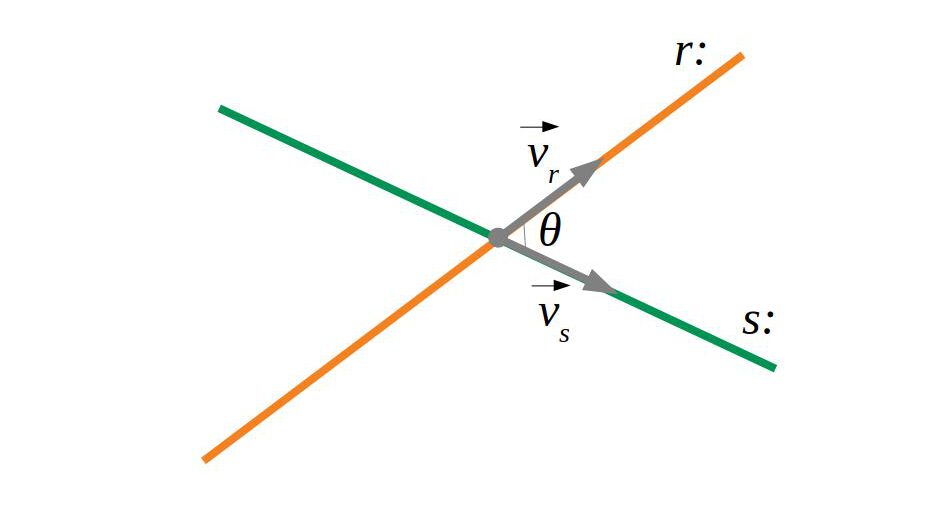
Per a calcular l’angle entre dos vectors fem:
\(\cos \theta=\frac{\vec u \cdot \vec v}{\left| u \right| \cdot \left| v \right|}\)
Exemple:
\(
\vec v_1(3,2,1), \; \vec v_2(-4,2,2)\\
\cos \theta=\frac{(3,2,1) \cdot (-4,2,2)}{\left|(3,2,1)\right| \cdot \left|(-4,2,2)\right|}\\
\cos \theta=\frac{-6}{\sqrt{14} \cdot \sqrt{24}}=-\frac{\sqrt{21}}{14}\\
\theta=\arccos {(-\frac{\sqrt{21}}{14})}=109.11^{\circ}
\)
6.2.1 Recta-recta
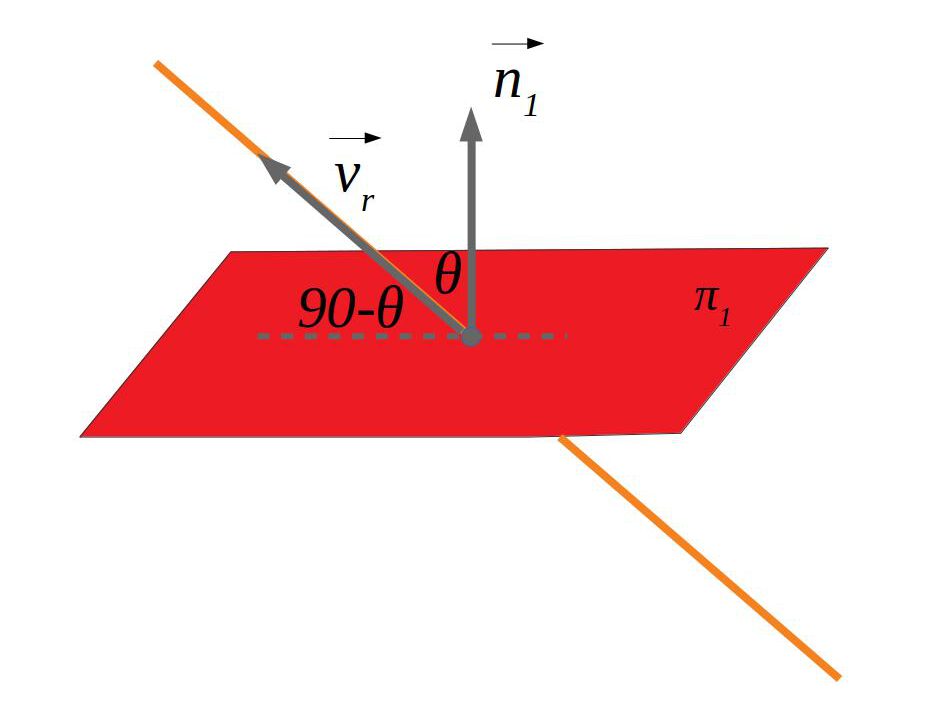
6.2.2 Recta-pla
L’angle entre la recta i el pla és \(90-\theta\). Aquest angle també es pot calcular directament fent \(\sin \theta=\frac {\vec u \cdot \vec v}{|\vec u| \cdot |\vec v|}\).
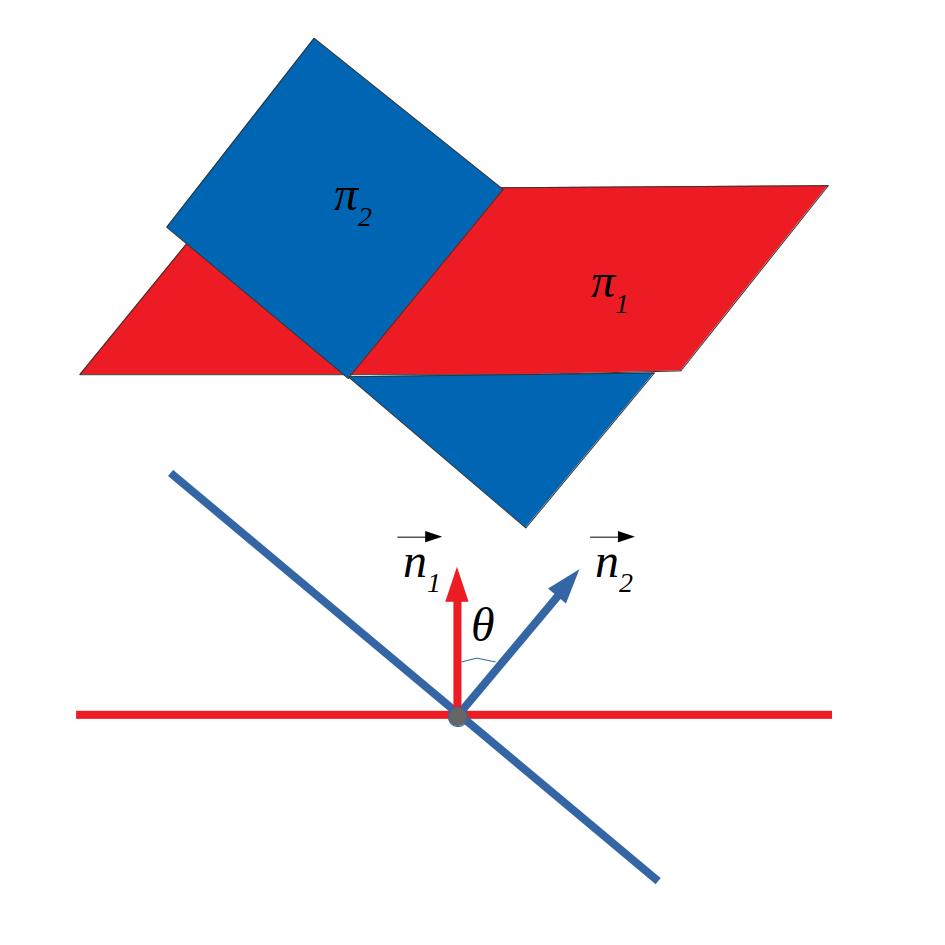
6.2.3 Pla-pla
Es calcula de la mateixa manera que l’angle entre dues rectes l’angle_entre dues rectes fent servir els vectors normals dels plans.
Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?
Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.