5.1 Representació a la recta real
i) Per a representar un nombre enter (\(\mathbb{Z}\)) a la recta real, la dividim en dues parts i a la dreta hi coloquem el nombre enters positius (\(\mathbb{N}\)) i a l’esquerra en negatius:

ii) Per a representar un nombre racional (\(\mathbb{Q}\)), primer calcularem la fracció generatriu i després la representaren a la recta real.
Les fraccions poden ser pròpies o impròpies:
En una fracció pròpia, el numerador és més petit que el denominador i, per tant, el nombre decimal serà un nombre entre \(0\) i \(1\) (p.e: \(\frac{4}{5}=0.8\)).
En una fracció impròpia, el numerador és més gran que el denominador i, per tant, el resultat és més gran que u (p.e \(\frac{5}{2}=2.5)\). Les fraccions impròpies són els nombre mixtos (\(\frac{5}{2}=2+\frac{1}{2}\)).
Exemple:
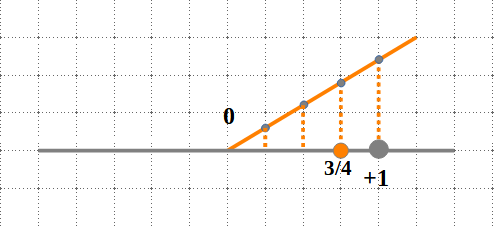
Calculem la fracció (pròpia) generatriu:
\(
0.75=\frac{75}{100}=\frac{3}{4}
\)
Per a representar la fracció (pròpia) a la recta real:
i) Dibuixem una línia qualsevol i la dividem en tantes parts iguals com indiqui el denominador, unim el darrer punt amb l’u i tracem paral·leles des de cada punt fins que tallin la recta real per tal de dividir el segment \( 0-1\) en parts iguals.
Si la fracció generatriu és impròpia, usarem el matexi procediment:
Exemple:
\(
1.75=\frac{175}{100}=\frac{7}{4}=2+\frac{3}{4}
\)
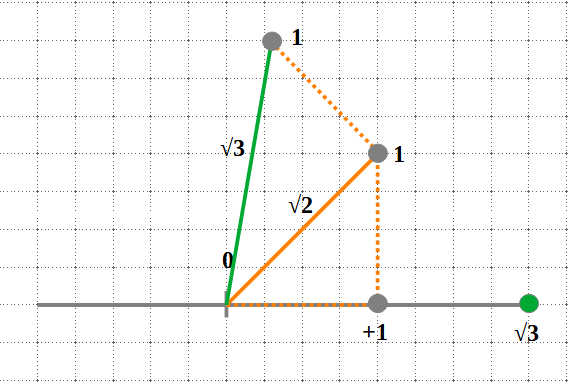
iii) Per a representar un nombre irracional, farem servir el Teorema de Pitàgores:
Exemple:
\(
\sqrt{2}=\sqrt{1^2+1^2}
\\
\sqrt{3}=\sqrt{(\sqrt{2})^2+1^2}
\)
6. Intervals
És un segment de la recta real que obtenim quan la fitem per dos extrems. L’extrem de l’esquerra és l’extrem inferior i el de la dreta el superior. La diferència entre els dos extrems és l’amplitud de l’interval.
Un extrem és obert quan format no part de l’interval i tancat si en forma part. Un interval amb els dos extrems oberts és un interval obert. Si té un extrem obert i l’altra tancat és un interval semiobert i si tots dos són tancats és un interval tancat.
Exemple:
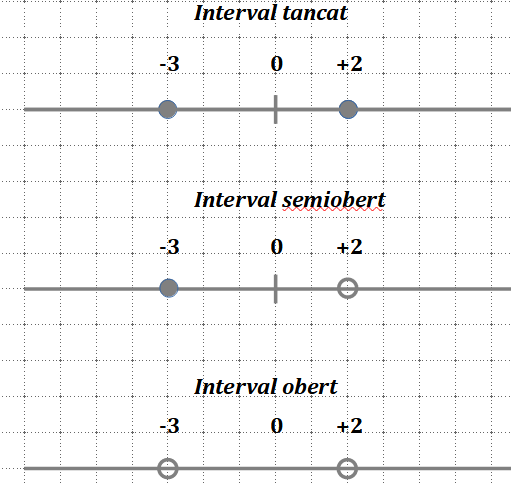
Escriurem els intervals anteriors amb notació algebraica de la següents forma:
\(-3\leq x\leq +2,\, -3\leq x \lt +2,\, -3\lt x\lt +2\). En una semirecta, l’extrem infinit sempre és un extrem obert (p.e, \((- \infty \lt x \leq +2]\)).
Escriurem els intervals anteriors amb notació d’interval de la següents forma:
\(\left[ -3,+2\right], \, \left] -3,+2\right], \left] -3,+2\right[\). \( ]n , n[\) o bé \((n , n)\) significa que l’extrem és obert i \( [n , n] \) vol dir que l’extrem és tancat. En una semirecta, un extrem és obert i l’altre tancat: \((-\infty, +2]\)).
7. Notació científica
És un nombre expressat segons la notació \(N*10^a\). \(N\) és un nombre decimal amb la part entera d’un sol dígit diferent de zero i \(a\) és un nombre enter.
Usem la notació científica per a expressar d’una manera més entenedora els nombres molt grans o molt petits.
Exemple:
\(
1 236 598 485 963=\, 1.236598485963*10^{+12} \\
0.0000000002568=\, 2.568*10^{-9}
\)
En el primer cas, hem desplaçat la coma 12 posicions cap a l’esquerra, és a dir, hem dividit el nombre per \(10^{-12}\). Per tant, per a mantenir l’equivalència del nombre, l’hem multiplicat per \(10^{+12}\).
En el segon cas, hem desplaçat la coma 9 posicions cap a la dreta, és a dir, hem multiplicat el nombre per \(10^{+9}\). Per tant, per a mantenir l’equivalència del nombre, l’hem dividit per \(10^{-9}\).
7.1 Operacions
Per a multiplicar o dividir dos nombres en notació científica, multipliquem o dividim els nombres i les potències de deu. Si el resultat no té la forma de notació científica, el transformarem perquè la tingui.
Exemple:
\(
2.56 10^{+5}*3.72 10^{-3}=\\
(2.56*3.72)*(10^{+5}*10^{-3})=\
9.4116*10^{+2}
\)
Per a sumar o restar nombre en notació científica, les potències de deu han de tenir el mateix exponent. Si l’exponent no és igual, transformarem un dels dos nombres perquè ho siguin.
Exemple:
\(
2.56 10^{+5}+3.72 10^{-3}=\\
(256 000 000 10^{-3}+3.72 10^{-3}=\\
256000003.7 10^{-3}=\\
2.560000037 10^{5}
\)
Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?
Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.