1. Equacions logarítmiques:
Són equacions que la incògnita és a l’argument d’un o més logaritmes (p.e:\(2*log(x+6)\)).
El logaritme és la funció inversa de les funcions exponencials (la inversa de les funcions potencials és la radicació): \(b^{exp}=n\) (potència), \( log_b(n)=exp\); \(2^3=8, , log_2(8)=3\).
El logaritme d’un nombre és l’exponent al qual hem d’elevar la base per obtenir el nombre. En aquest exemple, el logaritme de vuit en base dos és tres.
Els logaritmes foren inventats per John Napier a principis del segle XVII. La utilitat dels logaritmes és simplificar el càlcul quan hem d’operar amb nombres molt grans o molt petits.
Els logaritmes més comuns són els decimals o de base 10 ( \(log_{10}\) o \(log \)). Els logaritmes naturals o neperians ( \(log_e \) o \(Ln \)) tenen de base el nombre irracional \(e\).
1.1 Propietats dels logaritmes
Les propietats dels logaritmes són necessàries per a poder resoldre’n les equacions. Són les següents:
(Forma compacta = Forma desenvolupada)
\(
log_b(x*y)= log_b (x) + log_b (y)\\
log(2*3)=log(2)+log(3)\\
\\[1cm]
log_b (\frac{x}{y})= log_b (x) – log_b (y)\\
log(2*3)=log(2)-log(3)[1cm]
log_b (x^n)= n*log_b (x)\\
log (2^3)=3*log(2)\\
\\[1cm]
log_b (x<=0) \notin \enspace \mathbb{R}\\
log(0), log(-2) \notin \enspace \mathbb{R}.\\
\)
1.2 Resolució d’equacions amb un sol logaritme
La incògnita del logaritme pot ser la base, l’exponent o el nombre, però per a resoldre’l sense calculadora sempre farem l’antilogaritme o potència. El mètode de resolució d’equacions logarítmiques és:
1. Descomponem les bases compostes (que no són primeres)
2. Fem l’antilogaritme
3. Resolem l’equació
4. Comprovem el resultat.
\(
log_2(16)=x
\\
2^x=16
\\
2^x=2^4
\\
x=4
\\[1cm]
log_x(16)=4
\\
x^4=16
\\
x^4=2^4
\\
x=2
\\[1cm]
log_2(x)=4
\\
2^4=x
\\
x=16
\\[1cm]
log(3x+10)=4
\\
3x+10=10^4
\\
x=\frac{10^4-10}{3}
\\
x=3 330
\)
1.3 Amb més d’un logaritme
Si hi ha més d’un logaritme, no es podrà usar el mètode anterior de resoldre fent l’antilogaritme. En aquest cas, farem servir les propietats dels logaritmes per a transformar l’equació en la forma compacta equivalent i quan l’hagem transformat amb un sol logaritme, farem l’antilogaritme:
\(
log(x+1)+log(x-3)=log(5x-13)
\\
log[(x+1)*(x-3)]=log(5x-13)
\\
(x+1)*(x-3)=5x-13
\\
x^2-2x-3=5x-13
\\
x^2-7x+10=0
\\
x_1=5
\\
x_2=2
\\[1cm]
log_5(x+2)^4-1=log_5(x+2)+5
\\
log_5(x+2)^4-log_5(x+2)=5+1
\\
4*log_5(x+2)-log_5(x+2)=6
\\
3*log_5(x+2)=6
\\
log_5(x+2)=2
\\
x+2=5^2
\\
x=25-2=23
\)
En el primer exemple, \(x=2\) no és cap solució perquè l’argument de \(log(x-3), log(5x-13)\) és negatiu.
2. Equacions exponencials
Una equació és exponencial quan la incògnita és a l’exponent. Per a resoldre una equació exponencial usarem les propietats de les potències.
2.1 Propietats de les potències
Per a resoldre una equació potencial farem servir les propietats de les potències (recordeu que podem operar potències si tenen la mateixa base o el mateix exponent).
\(
a^n*a^m=a^{n+m}:
\\
2^6*2^9=2^{15}
\\[1cm]
a^n \div a^m=a^{n-m}
\\
2^{6} \div 2^9=2^{-3}
\\[1cm]
(a^n)^m=a^{n*m}
\\
(2^3)^9=2^{27}
\\[1cm]
a^0=1
\\
2^0=1,(\sqrt{2})^{ 0}=1, \pi^0=1, (-2)^0=1
\\[1cm]
a^1=a
\\
2^1=2
\\[1cm]
a^{-n}=\frac{1}{a^n}
\\
2^{-6}=\frac{1}{2^6}
\)
2.2 Resolució d’equacions exponencials
El mètode per a resolder equacions exponencials és el següent:
1. Descompondre les bases compostes en bases primeres
2. Trobar l’expressió potencial comuna a tots els termes
3. Fer el canvi d’aquesta expressió potencial comuna per t.
4. Resoldre l’equació resultant.
5. Desfer el canvi.
\(
2^{(x+3)}+4^{(x+1)}-320=0
\\
2^{(x+3)}+(2^2)^{(x+1)}-320=0
\\
2^{(x+3)}+2^{(2x+2)}-320=0
\\
2^x*2^3+(2^x)^2*2^2-320=0
\\
2^x=t
\\
4t^2+8t-320=0
\\
t=8, -10
\\
2^x=8
\\
x=3
\)
(Hem ignorat la solució \(t=-10\) perquè \(-10=2^x\) no es pot resoldre.)
3. Equacions trigonomètriques
Són equacions que tenen la incògnita en l’argument de funcions trigonomètriques. Per a resoldre-les, fem servir les identitats trigonomètriques.
3.1 Identitats trigonomètriques
IDENTITATS-TRIGONOMETRIQUES
3.2 Resolució d’equacions trigonomètriques
Tot i que no hi ha un mètode únic per a resoldre una equació trigonomètrica, en general es poden resoldre seguint el següent esquema:
1. Transformem les sumes en productes o els productes en sumes per tal de convertir els arguments amb més d’un angle en arguments amb un sol angle.
2. Transformem les funcions trigonomètriques derivades en les funcions trigonomètriques fonamentals (sin, cos).
3. Transformem tots els angles no simples de l’equació en simples.
4. Transformem tots els sinus a cosinus o a l’inrevés fent servir la identitat trigonomètrica fonamental (\(sin^2+cos^2=1\)).
5. Resolem l’equació trigonomètrica resultant.
Però l’ordre a seguir pot ser diferent per a cada equació trigonomètrica. Haurem d’avaluar en cada cas quin ordre s’ha de seguir per a resoldre l’equació de la millor manera.
Recordeu que el resultat d’una equació trigonomètrica es correspon amb dos angles i que també hi hem d’afegir els angles que es generen en cada volta completa a la circumferència (\(360*k, 2\pi*k\)). Per tant, la solució d’una equació trigonomètrica no és única, sinó que és una família de solucions:
\(
tg(\frac{\alpha}{2})=2
\\
arctg(2)=\alpha
\\
alpha=63.435º+360*k, k \in \mathbb{N}
\)
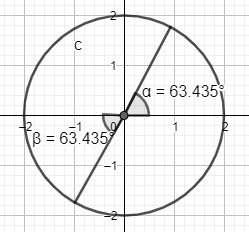
En aquest cas, simplifiquem una equació trigonomètrica amb més d’una funció i angles compostos en una equació d’una sola funció:
\(
{cos(2\alpha)+cos(\alpha)}*{sin(2\alpha)+sin(\alpha)}=0
\\
2cos^2{\alpha}-1+cos{\alpha}*2sin{\alpha}*cos{\alpha}+sin{\alpha}=0
\\
2*(1-sin^2{\alpha})-1+2sin{\alpha}*(1-sin^2{\alpha})+sin{\alpha}=0
\\
2-2sin^2{\alpha}-1+2sin{\alpha}-2sin^3{\alpha}+sin{\alpha}=0
\\
-2sin^3{\alpha}-2sin^2{\alpha}+3sin{\alpha}+1=0
\\
t=sin{\alpha}
\\
2t^3+2t^2-3t-1=0
\\
t=1,\frac{-2+\sqrt{2}}{2},\frac{-2-\sqrt{2}}{2}
\\
x=arcsin(t)=90º,-17.03º\\
\)
La tercera solució \(sin^{-1}(\frac{-2-\sqrt 2}{2})\) no és possible perquè \(\frac{-2-\sqrt 2}{2}=-1.707.\)
Demostrem una igualtat trignomètrica reduint les expressions de cada banda de la igualtat amb més d’una funció i angles compostos a una sola funció amb un angle simple:
\(
tg^2 \alpha-sin^2 \alpha=tg^2 \alpha*sin^2 \alpha
\\
\frac{sin^2\alpha}{cos^2\alpha}-sin^2\alpha=\frac{sin^2\alpha}{cos^2\alpha}*sin^2\alpha
\\
\frac{sin^2\alpha-sin^2\alpha*cos^2\alpha}{cos^2\alpha}=\frac{sin^4\alpha}{cos^2\alpha}
\\
sin^2\alpha-sin^2\alpha*(1-sin^2\alpha)=sin^4\alpha
\\
sin^2\alpha-sin^2\alpha+sin^4\alpha=sin^4\alpha
\\
sin^4\alpha=sin^4\alpha
\)
Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?
Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.