Anàlisi funcional

1. Definició

L’anàlisi matemàtic és la part de les matemàtiques que estudia les funcions.

Una funció és una una aplicació o correspondència \(f\) entre dos conjunts numèrics \((X,Y) (f: X \mapsto Y)\).

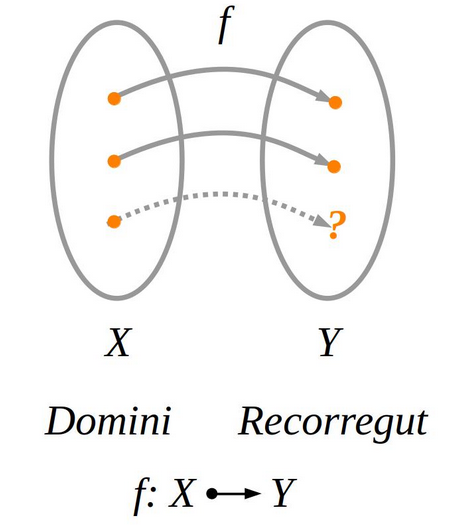
Per a determinar el comportament d’una funció, analitzem de \(-\infty\) fins a \(+\infty\) diverses característiques que un cop interpretades conjuntament ens mostraran aquest comportament.

2. Característiques

2.1 Domini i recorregut

El domini són tots els punts del conjunt inicial \(X\) als quals els correspon un o més valors del conjunts d’arribada \(Y\) (codomini o recorregut). Quan a un punt del conjunt \(X\) no li correspon cap punt del conjunt \(Y\), aquest punt no pertany al domini de la funció (la fletxa puntejada del diagrama de Venn anterior és un punt que no pertany al domini de la funció \(f(x)\)).

Per a determinar el domini d’una funció hem d’analitzar-la per tal de esbrinar si hi ha algun punt \(x\) al qual no li correspongui cap imatge (\(y\)).

Les funcions més habituals són: a) Les polinòmiques, les racionals i les irracionals (\(y=\sqrt[n]{P(x)}\)).

1. Polinòmiques: el domini de les funcions polinòmiques són tots els nombres reals \(Dom \, y=\{\forall \, x \in \mathbb{R}\}\)
2. Racionals \(y=\frac{N(x)}{D(x)}\): el domini de les funcions racionals son tots els nombre reals excepte els que fan el polinomi del denominador zero \(Dom \, y=\{\forall \, x \in \mathbb{R} / (D(x) \neq 0)\}\).
3. Irracionals \(y=\sqrt[2n]{P(x)}\): el domini de les funcions irracionals d’index de l’arrel parell, són tots els nombres reals excepte el que fan que el radicand sigui més petit que zero \(Dom \, y=\{\forall \, x \in \mathbb{R} / (P(x) \geq 0)\}\).
   
   Quan haguem resolt l’equació que resulta d’igualar el radicand a zero, haurem de determinar quin o quins dels intervals que divideixen la recta real són solució substituint un punt de cada interval: si la solució és negativa, l’interval no pertany al domini.

Exemples:

\(y= 4x³-2x²+8x-9\)

\(
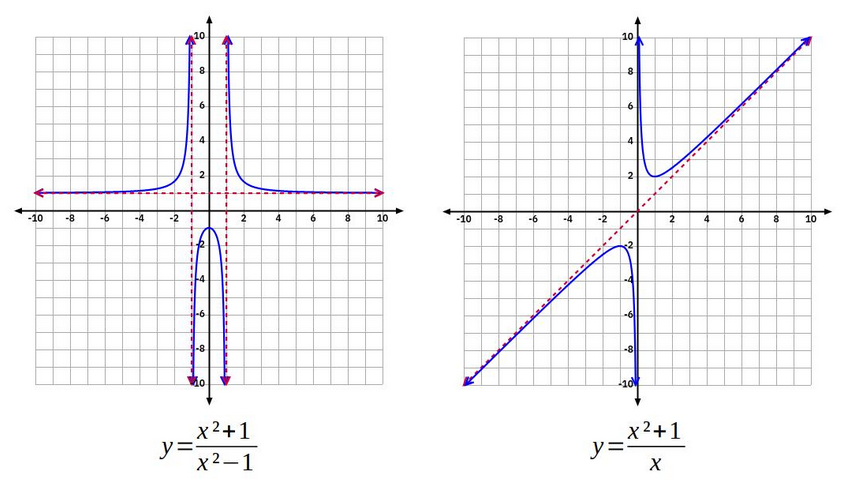
y= \frac{x²+1}{x²-1}\\
x²-1=0\\
x=\pm1\\
Dom \, y=\{\forall \, x \in \mathbb{R} / x²-1 \neq 0)\}, \text {o bé}\\
Dom \, y=\{\forall \, x \in \mathbb{R} / x \neq \pm1\}
\)

\(
y= \sqrt{x²-9}\\
x²-9=0\\
x=\pm3\\
y(-10)=\sqrt{(-10)²-9}>0\\
y(0)=\sqrt{(0)²-9}<0\\
y(+10)=\sqrt{(+10)²-9}>0\\
Dom \, y=\{\forall \, x \in \mathbb{R} / x²-9 > 0)\}, \text {o bé}\\
Dom \, y=\{\forall \, x \in \mathbb{R} – (x \geq -3, x \geq 3)\}
\)

Per a determinar el recorregut calcularem la funció inversa, tot i que de vegades no es pot calcular. En aquest cas, s’ha de dibuixar la funció per a poder de determinar-lo.

Exemple:

\(
y=\frac{x²+1}{x²-1}\\
y(x²-1)=x²+1\\
yx²-x²=1+y\\
x²(y-1)=1+y\\
x=\sqrt{\frac{1+y}{y-1}}
\)

Per a que la funció \(x=f(y)\) existeixi, s’ha de complir que el radicand de l’arrel sigui posItiu i el denominador diferent de zero: \(\frac{1+y}{y-1} \geq 0, y-1 \neq 0\)

Per tant, la funció no té imatge en \(-1 \leq y<+1\).

\(Rec(y)=(-\infty,-1]U(+1, -\infty)\).

(Vegeu l’entrada Funcions elementals per a saber-ne més.)

2.2 Monotonia i punts singulars

Vegeu l’entrada d ‘Aplicacions de les derivades, Monotonia i punts singulars.

\(
y=\frac{x²+1}{x²-1}\\
y’=\frac{2x(x²-1)-2x(x²+1)}{(x²-1)^2}\\
y’=0=2x(x²-1)-2x(x²+1)=-4x\\
x=0\\
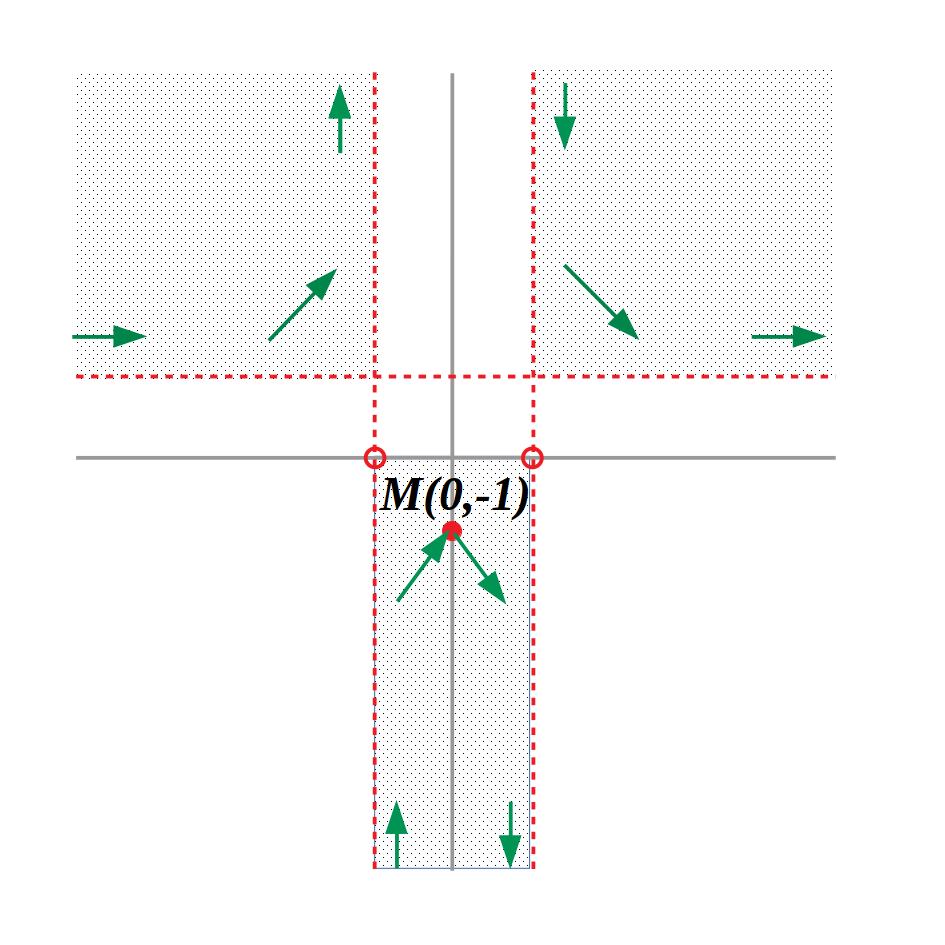
y(0)=-1\\[1cm]
y'(-10)=-4.-10>0 (creixent)\\
y'(+10)=-4.+10<0 (decreixent)\\
{Màxim (0,-1)}
\)

2.3 Curvatura i punts d’inflexió

Vegeu l’entrada d’Aplicacions de les derivades, Curvatura i punts d’inflexió.

\(
y=\frac{x²+1}{x²-1}\\
y’=-4x\\
y”=-4 \enspace (curvatura \enspace negativa)
\)

La funció no té punts d’inflexió.

2.4 Asímptotes

Una asímptota és una recta a la qual la funció s’aproxima infinitesimalment (“infinitesimal: quantitat infinitament petita”) sense arribar a tallar-la mai. La funció i l’asímptota són tangents a l’infinit.

Quan calculem les asímptotes verticals d’una funció, haurem de calcular-ne també els límits laterals per tal de d’esbrinar el sentit de la corba (\(+\infty, -\infty)\) a cada banda de l’asímptota.

2.4.1 Asímptota vertical

Definició: \(lim_{x \rightarrow a} f(x)= \infty\)

Exemple:

\(
y=\frac{x²+1}{x²-1}\\
lim_{x \rightarrow a} \frac{x²+1}{x²-1}=\infty\\
x²-1=0\\
x=\pm 1
\\[1cm]
lim_{x \to +1^{-}}\frac{x²+1}{x²-1}=\frac{(0.009)²+1}{(0.009)²-1}=-\infty\\
lim_{x \to +1^{+}}\frac{x²+1}{x²-1}=\frac{(1.001)²+1}{(1.001)²-1}=+\infty
\\[1cm]
lim_{x \to -1^{+}}\frac{x²+1}{x²-1}= \frac{(-0.009)²+1}{(-0.009)²-1}=-\infty\\
lim_{x \to -1^{-}}\frac{x²+1}{x²-1}=\frac{(-1.001)²+1}{(-1.001)²-1}=+\infty\\
\)

2.4.2 Asímptota horitzontal

Definició: \(lim_{x \rightarrow \infty} f(x)=a\)

Exemple:

\(
lim_{x \rightarrow \infty} \frac{x²+1}{x²-1}=+1\\
y=1
\)

2.4.3 Asímptota obliqua

Definició: \(lim_{x \rightarrow \infty} \frac{f(x)}{x}=m, \enspace lim_{x \rightarrow \infty} f(x)-m=n\)

Exemple:

\(
m=lim_{x \rightarrow \infty} {\frac{x²+1}{x²-1}}:{x}\\
lim_{x \rightarrow \infty} \frac{x²+1}{(x²-1)*x}\\
lim_{x \rightarrow \infty} \frac{x²+1}{(x³-x)}=0
\)

No hi ha asímptotes obliqües.

Un altre exemple:

\(
m=lim_{x \rightarrow \infty} {\frac{x²+1}{x}}:{x}\\
lim_{x \rightarrow \infty} \frac{x²+1}{(x)*x}\\
lim_{x \rightarrow \infty} \frac{x²+1}{(x²)}=1\\
n=lim_{x \rightarrow \infty} f(x)-m\\
lim_{x \rightarrow \infty} \frac{x²+1}{x}-1*x\\
lim_{x \rightarrow \infty} \frac{x²+1-1*x²}{x}\\
lim_{x \rightarrow \infty} \frac{1}{x}=0\\
\textbf {y=x}
\)

Vegeu l’entrada Límits i continuïtat per a saber-ne més.

2.5 Punts de tall

Anomenem punts de tall als punts en els quals la funció talla els eixos de coordenades.

2.5.1 Amb les abscisses

Quan una funció talla l’eix de les \(x\), \(y=0\).

Exemple:

\(
y=\frac{x²+1}{x²-1}\\
0=\frac{x²+1}{x²-1}\\
x²+1=0, x=\sqrt{-1}
\)

No hi ha punts de tall amb l’eix de les \(x\).

2.5.2 Amb les ordenades

Quan una funció talla l’eix de les \(y\), \(x=0\).

Exemple:

\(
y=\frac{x²+1}{x²-1}\\
y=\frac{0²+1}{0²-1}=-1\\
(0,-1)
\)

2.6 Signe de la funció

El signe de la funció és el signe positiu o negatiu que tenen les imatges de la funció en cada interval del domini.

Per a determinar-ne el signe, determinarem el signe de la imatge d’un punt qualsevol de cada interval del domini.

Exemple:

\(
y=\frac{x²+1}{x²-1}\\[1cm]
(-\infty,-1)\\
y(-10)=\frac{(-10)²+1}{(-10)²-1}>0\\[1cm]
(-1,+1)\\
y(0)=\frac{(0)²+1}{(0)²-1}<0\\[1cm]
(+1,+\infty)\\
y(+10)=\frac{(+10)²+1}{(+10)²-1}>0\\
\) \(
(-\infty,-1)U(+1,+\infty):+\\
(-1,+1):-
\)

2.7 Simetria

Analitzem dos tipus de simetria, la parella i la senars.

2.7.1 Simetria parella

Una funció té simetria parella si es simètrica respecte a l’eix \(x=0\): \(f(x)=f(-x)\).

Exemple:

\(
y=\frac{x²+1}{x²-1}\\
f(x)=\frac{x²+1}{x²-1}\\
f(-x)=\frac{(-x)²+1}{(-x)²-1}=\frac{x²+1}{x²-1}\\
f(x)=f(-x) \enspace (Simetria \enspace parella).
\)

2.7.2 Simetria senars

Una funció té simetria senars si ho és respecte al punt \((0,0)\): \(f(x)=-f(-x)\).

Exemple:

\(
y=\frac{x²+1}{x}\\
f(x)=\frac{x²+1}{x}\\
-f(-x)=-\frac{(-x)²+1}{(-x)}=-\frac{x²+1}{(-x)}=\frac{x²+1}{x}\\
f(x)=-f(-x) \enspace (Simetria \enspace senars).
\)

2.8 Periodicitat

Una funció és periòdica si \(f(x)=f(x+T)\). Tot i que hi ha més funcions periòdiques, considerarem sols les trigonomètriques.

3. Gràfica

Per a dibuixar la gràfica de la funció representarem les característiques que hem determinat en un sistema de coordenades:

Exemple:

\(y=\frac{x²+1}{x²-1}\)

1. Domini: \((-\infty,-1)U(-1,+1)U(+1,+\infty)\)
2. Recorregut: \((-\infty,-1]U(+1,+\infty) \)
3. Monotonia/ Punts singulars: \((-\infty,-1)U(-1,0) \uparrow, \enspace (0,+1)U(+1,+\infty) \downarrow/ \enspace M(0,-1)\)
4. Curvatura/ Punts d’inflexió: \(Negativa/ \enspace No \enspace en \enspace té.\)
5. Asímptotes: \(x=\pm1,y=+1\)
6. Punts de tall: \((0,-1)\)
7. Signe: \((-\infty,-1)U(+1,+\infty)>0, \enspace (-1,+1)<0 \)
8. Simetria: \(Parella\)
9. Periodicitat: \(No \enspace és \enspace periòdica\)