Definició
La trigonometria és l’àrea de les matemàtiques que estudia la relació entre els costats i els angles dels triangles.
S’aplica sols als triangles rectangles, tot i que ens serveix per a resoldre qualsevol mena de triangle.
La paraula prové del grec: tri (tres), gono (angle) i metria (mesura).
Classificació dels triangles
Un triangle és una figura geomètrica plana de tres costats i tres angles.
Podem classificar els triangles segons els angles o els costats que els formen.
Segons els angles que els formen, es classifiquen en acutangles, rectangles i obtusangles.
Segons els costats que els formen, es classifiquen en isòsceles, equilàters i escalens.
(Vegeu l’entrada càlcul de l’àrea d’un polígon per a saber-ne més).
Mesura d’angles
Els angles tenen diferents unitats de mesura. La més coneguda és el grau sexagesimal. En una circumferència divida en graus sexagesimals cada quart de circumferència són 90º i una volta sencera són 360º.
El radià és la unitat d’angle del SI. Un radià és l’angle que té un arc de circumferència igual al radi \(s=r\).
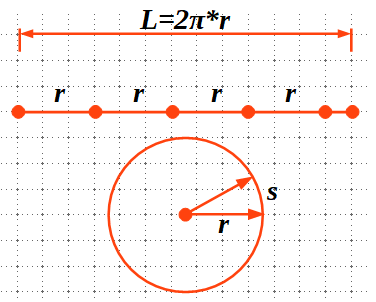
Com que la longitud de qualsevol circumferència és \(L=2\pi*r \Rightarrow \, 2\pi=\frac{L}{r}\).
Això vol dir que la longitud de qualsevol circumferència conté \(2\pi\) vegades el radi.
Cada partició d’un radi de la longitud d’una circumferència és un radià.
Quan mesurem els angles en radians, cada quart de circumferència són \(\frac{\pi}{2}\) radians (escrit \(rad\)). Una volta sencera són \(2\pi \enspace rad\) o simplement \(2\pi\).
Per passar de graus sexagesimals a radians usem el factor de conversió \(360º = 2\pi \, rad\).
Exemple:
\(30º.\frac{2\pi}{360º} = \frac{\pi}{6}\, rad\).
Els angles notables (més importants) són: \(0º\, (0\, rad),\, 30º\ (\frac{\pi} {6} \, rad), \, 45º\, (\frac{\pi}{4} \, rad), \,60º [latex]\frac{\pi}{6}\) \, 90º \, \((\frac{\pi}{2} \, rad)\).
Raons trigonomètriques
Una raó o proporció trigonomètrica és el quocient de la longitud de dos costats d’un triangle rectangle.
Definim les raons trigonomètriques fonamentals o bàsiques per a un angle qualsevol de la circumferència goniomètrica (la circumferència per a mesurar angles) com:
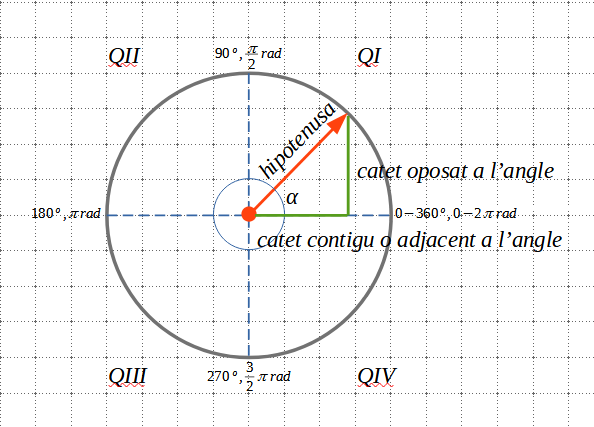
\(sin \, \alpha= \frac {catet \, oposat}{hipotenusa}\\\)
\(cos \, \alpha= \frac {catet \, contigu \, o \, adjacent}{hipotenusa}\)
Per a qualsevol triangle rectangle també es compleix que:
\(
hipotenusa^2 = catet \, oposat^2 + catet \, adjacent^2
\,
(a^2=b^2+c^2)
\)
I la relació derivada:
\(tan \, \alpha= \frac {catet \, oposat}{catet \, contigu\, o\, adjacent}\)
Les resta de relacions (proporcions o raons) trigonomètriques derivades del sinus i cosinus d’un angle són:
\(
cosecant \, d’ \alpha \,(csc \, \alpha) =\frac{1}{sin \, \alpha}= \frac{a}{b}
\\
secant \, d’ \alpha \,(sec \, \alpha) =\frac{1}{cos \, \alpha}=\frac{a}{c}
\\
cotangent \, d\, ‘ \alpha \, (cot \, \alpha) = \frac{1}{tan \, \alpha}=\frac{c}{b}
\)
Exemple:
Si \(a = 5, \,b = 3, \,c = 4\), llavors
\(
\sin\, \alpha = \frac{b}{a} = \frac{3}{5} = 0.6\\
\cos\, \alpha = \frac{c}{a} = \frac{4}{5} = 0.8\\
\tan\,\alpha = \frac{b}{c} = \frac{3}{4} = 0.75\\
\csc\, \alpha = \frac{a}{b} = \frac{5}{3} = 1.6667\\
\sec\, \alpha = \frac{a}{c} = \frac{5}{4} = 1.25\\
\cot\, \alpha = \frac{c}{b} = \frac{4}{3} = 1.333
\)
Les funcions inverses ens serveixen per a trobar l’angle sabent els valor de la funció.
Exemple:
\(
\alpha=\ arcsin \, \alpha\, (\sin^{-1} \, \alpha); \,
\arcsin{0.6} \,(\sin^{-1}{0.6})=36.87º
\\
\alpha=\ arccos \, \alpha\, (\cos^{-1} \, \alpha); \,
\arccos{0.6} \,(\cos^{-1}{0.6})=53.13º
\\
\alpha=\ arctan \, \alpha\, (\tan^{-1} \, \alpha); \,
\arctan{0.6} \,(\tan^{-1}{0.6})=30.96º
\)
I la taula de relacions trigonomètriques notables és:
| \(0º (0 \, rad)\) | \(30º (\frac{\pi}{6} \, rad)\) | \(45º (\frac{\pi}{4} \, rad)\) | \(60º (\frac{\pi}{3} \, rad)\) | \(45º (\frac{\pi}{2} \, rad)\) |
| \(\\sin \, \alpha\) | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt2}{2}\) | \(\frac{\sqrt3}{2}\) | \(1\) |
| \(\\cos \, \alpha\) | \(1\) | \(\frac{\sqrt3}{2}\) | \(\frac{\sqrt2}{2}\) | \(\frac{1}{2}\) | \(0\) |
| \(\\tan \, \alpha\) | \(0\) | \(\frac{1}{\sqrt3}\) | \(1\) | \({\sqrt3}\) | \(\infty\) |
Reducció d’angles al primer quadrant
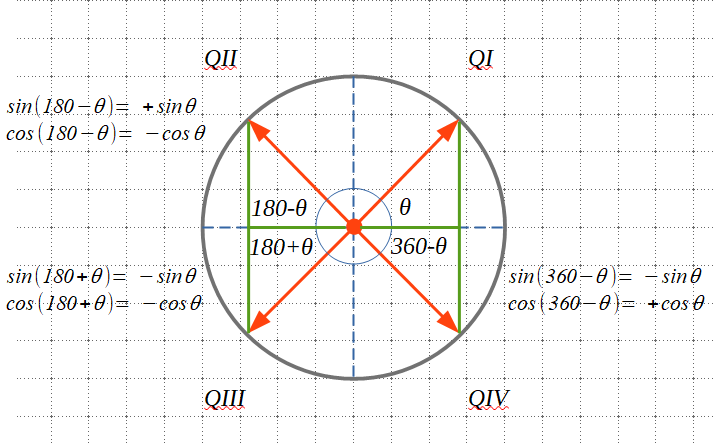 Reducció d’angles al primer quadrant
Reducció d’angles al primer quadrantLa reducció d’un angle al primer quadrant consisteix en transformar un angle de més de 90º a un altre del primer quadrant que tingui la mateixa obertura.
Un angle més gran de 360º es pot transformar en un angle de la primera volta de la següent manera:
Si \(\alpha= 1 285º\): el quocient de \(1 285 \div 360= 3\) i el residu és \(205º\). Això vol dir que \(1 285º\) equivalen a 3 voltes senceres a la circumferència més 205º addicionals a la quarta volta.
Un cop hem determinat quan val l’angle de la darrera volta incompleta, fem la reducció d’aquest angle al primer quadrant. Observant el gràfic superior, veiem que:
Per a un angle de segon quadrant: \(\theta_{q2}=180º – \theta_{q1}\\\)
Per a un angle de tercer quadrant: \(\theta_{q3}= 180º+\theta_{q1}\\\)
Per a un angle de quart quadrant: \(\theta_{q4}= 360º – \theta_{q1}
\).
Ailant \(\theta_1\), tenim la reducció de l’angle al primer quadrant.
Exemple:
Si \(\theta_{q2} = 135º \, \Rightarrow \, \theta_{q1}=180º – 35º = 45º\\\)
Si \(\theta_{q3} = 200º \, \Rightarrow \, \theta_{q1}=200º – 180º = 20º\\\)
Si \(\theta_{q4} = 350º \, \Rightarrow \, \theta_{q1}=360º – 350º =10º\)
I els signes de les relacions trigonomètriques de cada quadrant són:
\(sin \, \theta_{q1}: +, \, cos \, \theta_{q1}: +, \, tan \, \theta_{q1}: +\)
\(sin \, \theta_{q2}: +, \, cos \, \theta_{q2}: -, \, tan \, \theta_{q2}: \, –\)
\(sin \, \theta_{q3}: -, \, cos \, \theta_{q3}: -, \, tan \, \theta_{q3}: +\\
sin \, \theta_{q4}: -, \, cos \, \theta_{q4}: +, \, tan \, \theta_{q4}: \, –\)
Resolució de triangles
Semblança de triangles
Dos triangles són semblants quan es compleix que:
1. Els seus angles són iguals: \(\hat{A} = \hat{A’}, \hat{B} = \hat{B’}, \hat{C} = \hat{C’}\), i que
2. Els seus costats són proporcionals: \(\frac{a}{a’} = \frac{b}{b’} = \frac{c}{c’}\).
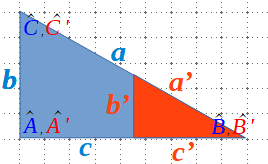 Triangles semblants
Triangles semblants
Resoldre un triangle consisteix a trobar el valor de tots els seus costats i angles. Els diferents triangles que haurem de resoldre són:
i) Un triangle rectangle,
ii) un triangle inscrit en un altre triangle
iii) un triangle obtusangle.
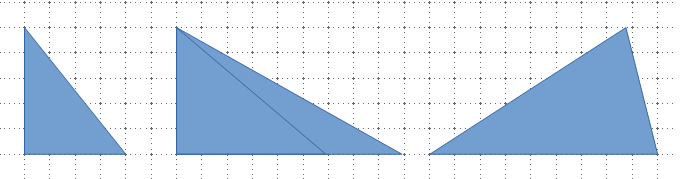
Per a resoldre els triangles anteriors farem servir la trigonometria i la semblança de triangles:
i) Un triangle rectangle:
Per a resoldre un triangle rectangle ens calen, o bé dos costats, o bé un costat i un angle. Farem servir les relacions trigonomètriques sinus, cosinus, tangent i el teorema de Pitàgores:
Exemple:
\(c=3, \, \hat B=30º \Rightarrow \, a=\frac{c}{cos\, 30º}= 2 \sqrt 3, \, b=\sqrt{a^2-c^2}=\sqrt 3\)
Exemple:
\(c=3, \,a=2\sqrt3 \Rightarrow \, b=\sqrt{a^2-c^2}=\sqrt 3, \, \hat B=tg^{-1}(\frac{b}{c})=30º\)
Per a trobar l’angle complementari del \(\hat B\) farem \(90-\hat B=60º\).
ii) Dos triangles rectangles inscrits:
En aquest cas, farem la tangent de cada triangle rectangle i resoldrem el sistema pel mètode d’igualació:
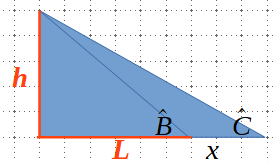
Exemple:
\(
x=5 m, \, \hat B=40º, \, \hat C=20º, \, (L=?, \, h=?) \\
\begin{cases}
\tan \hat B=\frac{h}{L}\\
\tan \hat C=\frac{h}{L+x}
\end{cases} \\
h=\tan \hat B*L=\tan \hat C*(L+x)\\
L=\frac{\tan \hat C*x}{\tan \hat B-\tan \hat C }\\
L=\frac{tan 20º*5}{tan 40º-tan 20}=3.83 m\\
h= \tan \hat B*L=tan 40º*3.83= 3.21 m
\)
iii) Un triangle obtusangle:
Usarem també el mètode anterior:
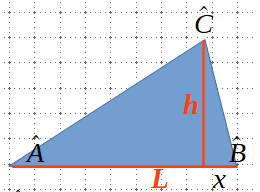
Exemple:
\(
L=15 m, \, \hat A=40º, \, \hat B=20º, \, (x=?, \, h=?) \\
\begin {cases}
\tan \hat A=\frac{h}{L-x}\\
\tan \hat B=\frac{h}{x}
\end {cases}\\
x=\frac{L*tan \hat A}{tan \hat A+\tan \hat B}\\
x=\frac{15*(tan 40º)}{tan 40º+tan 20º}=10.46 m\\
h=x*\tan \hat B= 10.46*tan 20º=3.81 m
\)
Altres mètodes de resolució
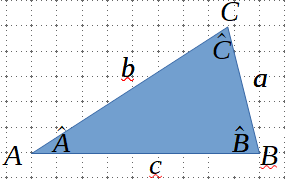
Teorema del cosinus
Fem servir el teorema del cosinus si coneixem tres costats o dos costats i l’angle que els separa. També el podem usar per a calcular l’angle que els separa si coneixem dos costats adjacents.
Qualsevol triangle d’angles \(\hat{A}, \hat{B}, \hat{C}\) i costats \(a, b, c\) compleix que (teorema del cosinus):
\(a^2 = b^2 + c^2 – 2*b*c\cos\hat{A}\)
\(b^2 = a^2 + c^2 – 2*a*c*\cos\hat{B}\)
\(c^2 = a^2 + b^2 – 2*a*b*\cos\hat{C}\)
Exemple:
Si coneixem els tres costats (ens cal esbrinar els tres angles): \(a = 7, b = 3, c = 6\)
Trobem dos angles:
\(
a^2 = b^2 + c^2 – 2*b*c*\cos\hat{A}\\
7^2 = 3^2 + 6^2 – 2*3*6*\cos\hat{A}\\
\cos\hat{A} = -\frac{7^2-3^2-6^2}{2*3*6}=\frac{1}{9}\\
\hat{A} = \cos^{-1}{(\frac{1}{9})}=96.38º
\)
Exemple:
Si coneixem dos costats i l’angle que el separa: \(a = 7, b = 3, \hat C=58º\)
\(
c^2 = a^2 + b^2 – 2*a*b*\cos\hat{C}\\
c^2 = 7^2 + 3^2 – 2*7*3*\cos\hat{58}\\
c=5.99 m
\)
Per a trobar \(\hat A, \, \hat B\), seguim el procediment anterior:
\(
\hat A=\cos^{-1}{\frac{a^2-b^2-c^2}{-2*b*c}}=93.38º\\
\hat B=\cos^{-1}{\frac{b^2-a^2-c^2}{-2*a*c}}=25.21º
\)
Teorema del sinus
Qualsevol triangle d’angles \(\hat{A}, \hat{B}, \hat{C}\) i costats \(a, b, c\) compleix que: \(\frac{a}{\sin\hat{A}} = \frac{b}{\sin\hat{B}} = \frac{c}{\sin\hat{C}}\)

Usem el teorema del sinus quan coneixem, o bé dos costats i l’angle oposat d’un dels costats coneguts, o bé dos angles i un costat oposat d’un dels angles coneguts del triangle.
Exemple:
Coneguts un costat i dos angles: \(\hat{A} = 62º, \hat{B} = 47º, c = 9\)
Trobem l’angle que falta sabent que tots tres sumen 180:
\(\hat{C} = 180 – 62 – 47 = 71º\)
Apliquem el teorema del sinus per trobar els altres dos costats:
\(
\frac{a}{\sin\hat{A}} = \frac{b}{\sin\hat{B}}= \frac{c}{\sin\hat{C}}\\
\frac{a}{\sin 62º}=\frac{b}{\sin 47} = \frac{9}{\sin71º}\\
\frac{a}{\sin 62º} = \frac{9}{\sin71º}\\
a = 9*\frac{\sin 62}{\sin 71}=8.4\\
\frac{b}{\sin 47} = \frac{9}{\sin71º}\\
b = 9*\frac{\sin 47}{\sin 71}=6.96
\)
Teorema de l’altura
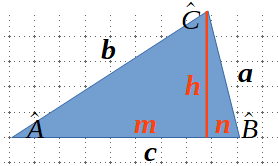 \(h^2 = m*n\)
\(h^2 = m*n\)
Teorema del catet
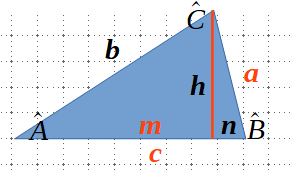 \(c^2 = a*m\)
\(c^2 = a*m\)
Equacions trigonomètriques
Per a resoldre equacions trigonomètriques hem d’usar les identitats trigonomètriques.
(Vegeu l’entrada equacions trigonomètriques per a saber-ne més).
Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?
Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.