Un nombre complex té la forma \(z=a+bi\). Diem que \(a\) és la part real del nombre i \(b\) és la part imaginària del nombre (per exemple, \(1 – i, 3 + \sqrt{5}i, -7 + 5i, -\frac{3}{4} – 4i, \sqrt{2} + i\)). \(a\) i \(b\) són nombres reals. \(i\) és part de la solució de l’equació \(x^2=-1=i^2\).
Els nombres complexos es van inventar per a poder calcular les arrels negatives d’exponent parell (\(\sqrt{-4}, \, \sqrt[6]{-100}\), etc.) que no tenen solució en el conjunt dels nombres reals \(\mathbb{R}\).
Però si definim un nombre nou de manera que el seu quadrat sigui negatiu haurem resolt el problema. Aquest nombre és \(i = \sqrt{-1}\) i el seu quadrat val \(-1\):
Veiem-ho amb un exemple:
\(
x^2 + x + 1 = 0:
\\
x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}
\\
\frac{-1\pm\sqrt{1^2-4*1*1}}{2*1}
\\
\frac{-1 \pm \sqrt{-3}}{2}
\\
\frac{-1 \pm \sqrt{3i^2}}{2}
\\
\frac{-1 \pm i\sqrt{3}}{2}
\)
Per a representar els nombres reals fem servir la recta real, però per a representar gràficament els nombres complexos ens calen dues dimensions i hem de fer-ho al pla.
Situarem la part real d’un nombre complex (\(a\)) a l’eix d’abcisses i la part imaginària (\(b\)) a l’eix de ordenades.
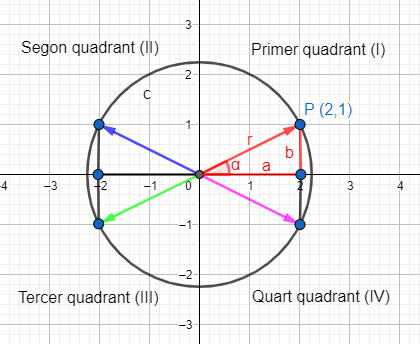
Per exemple, si volem representar:
\(
\color{red}{z = 2 + 1i\, (a=2, b=1)}\\
\color{blue}{z = -2 + 1i\, (a=-2, b=1)}\\
\color{green}{z = -2 – 1i\, (a=-2, b=-1)}\\
\color{magenta}{z = 2 – 1i\, (a=2, b=1)}
\)
Binòmica
La forma binòmica (\(z = a + bi \, ( a,b \in \mathbb{R}\)) és la forma més habitual de representar un nombre complex. Existeixen dos casos especials de nombres complexos:
- Reals purs \(b = 0, \, z=a\): són els nombres reals \(\mathbb{R}\). Per tant, els nombres reals són un subconjunt dels nombres complexos \(\mathbb{C}\).
Exemple: \(z=2+0i=2\)
- Imaginaris \(a = 0, \, z=bi\): són els imaginaris purs.
Exemple: \(z=0-3i=-3i\)
El conjugat d’un nombre complex \(z\) és \(\bar{z} = a – bi\). L’obtenim canviant el signe de la part imaginària.
Quan resolem equacions de segon grau de discriminant negatiu les solucions són sempre dos nombres complexos conjugats (\(z\) i \(\bar{z}\)). Diem que \(z\) i \(\bar z\) són les solucions conjugades de l’equació.
L’oposat d’un nombre complex \(z\) és aquest nombre canviat de signe, \(-z= -(a + bi) = -a – bi\).
Polar
La notació d’un nombre complex en forma polar és \(z=r_{\alpha}\).
- El mòdul de \(z\) és la distància que hi ha entre el punt \(P(a,b)\) i l’origen de coordenades. Coincideix amb el radi de la circumferència: \(r = |z| = \sqrt{a^2 + b^2}\).
- L’argument de \(z\) és l’angle que forma el vector associat al punt \(z\) amb l’eix de les \(x\): \(\alpha=\arctan ( \frac{b}{a})\).
Tranformacions
Per a canviar entre la notació binòmica i la polar, fem el següent:
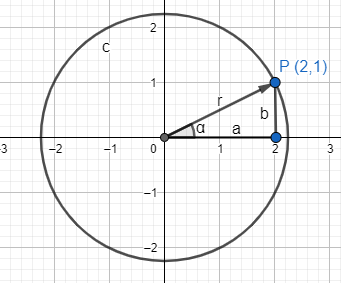
De binòmica a polar:
\(
r=\sqrt{a^2+b^2}\\
\alpha=arctan(\frac{b}{a})\)

De polar a binòmica:
\(
a=r*cos \alpha\\
b=r*sin \alpha
\)
Trigonomètrica
La notació trigonomètrica d’un nombre complex \([z=r*(\cos \alpha \pm i\sin \alpha)]\) s’obté substituint \(a\) i \(b\) per les expressions trigonomètriques respectives \(a=r*cos \alpha, \,b=r*sin \alpha\):
\(z =(a \pm bi)=(r*cos \alpha \pm r*sin \alpha)=r*(\cos \alpha \pm i\sin* \alpha)\).
Les operacions bàsiques entre dos nombres complexos \(z_{1} = a + bi\) i \(z_{2} = c + di\), són:
En forma binòmica
Suma/ resta
\(z_{1} + z_{2} = (a + bi) + (c + di) = (a + c) + (b + d)i\)
\(z_{1} – z_{2} = (a + bi) – (c + di) = a + bi – c – di = (a – c) + (b – d)i\)
Exemple:
\(
(3 + 4i)+(-2 + 5i) = [(3-2)+(4+5)i]=(1+9i)\\
(3 + 4i)-(-2 + 5i) = [(3+2)+(4-5)i]=(5-1i)\\
\)
Producte
\(
z_{1}*z_{2} = (a + bi)(c + di) = ac + adi + bci + bdi^2 =\\
ac + adi + bci – bd = (ac – bd) + (ad + bc)i
\)
Exemple:
\(
(3 + 4i)*(-2 + 5i)=3*(-2)+3*5i+4i*(-2)+4i*5i=\\
-6+15i-8i+20i^2=6-20+15i-8i=-14+7i
\)
Divisió
Com en el cas dels radicals o dels vectors, tampoc sabem dividir dos nombres complexos. Per a convertir el denominador en un nombre real i poder fer la divisió, fem servir la identitat notable \((x-a)*(x+a)=(x)^2-(a)^2\) :
\(\frac{z_{1}}{z_{2}} = \frac{(a + bi)}{(c + di)} = \frac{(a + bi)}{(c + di)}\frac{c – di}{c – di} = \frac{(a + bi)(c – di)}{(c + di)(c – di)} = \frac{(a + bi)(c – di)}{c^2 + d^2} = \frac{(ac + bd) + (bc – ad)i}{c^2 + d^2} = \frac{ac + bd}{c^2 + d^2} + \frac{bc – ad}{c^2 + d^2}i\)
Exemple:
\(
\frac{(3 + 4i)}{(-2 + 5i)}=\frac{(3 + 4i)}{(-2 + 5i)}*\frac{(-2-5i)}{(-2 -5i)}=
\\
\frac{(3 + 4i)*(-2+5i)}{(-2+5i)*(-2 – 5i)}=\frac{(14-23i)}{(-2)^2-(5i)^2}=
\\
\frac{(14-23i)}{4-25i^2}=\frac{(14-23i)}{29}=\frac{14}{29}+\frac{-23}{29}i
\)
En forma polar
Suma/ resta
La suma i la resta de dos nombres complexos es fa sempre en forma bionòmica, no es pot fer en forma polar.
Producte
\(z_{1}*z_{2} = r_{\alpha}*s_{\beta} = (r*s)_{\alpha + \beta}\).
El mòdul del nombre complex resultant és el producte dels mòduls i l’argument és la suma dels arguments.
Exemple:
\(6_{35}*8_{25}=(6*8)_{35+25}=48_{60}\)
Divisió
\(\frac{z{1}}{z_{2}} = \frac{r_{\alpha}}{s_{\beta}} = (\frac{r}{s})_{\alpha – \beta}\).
És a dir, el mòdul del nombre complex resultant és el quocient dels mòduls, i l’argument és la resta dels arguments.
Exemple:
\(40_{35} \div 8_{25}=(\frac{40}{8})_{35-25}=5_{10}\)
Potències
\( (r_{\alpha})^n = (r^n)_{n\alpha}\).
Exemple:
\((5_{53})^3=(5^3)_{3*53}=125_{159}\)
Radicació
Per a fer la radicació d’un nombre complex primer el transformarem a la forma polar: \(r=\sqrt{a^2+b^2} \, \alpha=arctan(\frac{b}{a})\). A continuació, farem la radiació de la següent manera:
\(
\sqrt[n]{r}_{\alpha}=s_{\beta} \, \Rightarrow r_{\alpha}=(s^n)_{n\beta}\\
\begin {cases}
r =s^n \, \Rightarrow s=\sqrt[n]{\left|r \right |}\\
\alpha=n*\beta \, \Rightarrow \beta= \frac{\alpha}{n}
\end {cases}
\).
\(\beta_n=\frac{\alpha+2\pi*k}{n}\), o bé \(\beta_n=\frac{\alpha+360*k}{n} \, (k=0,1,2…)\)
Exemple:
Volem calcular \(\sqrt[3]{-8} \, ,(n=3, r=-8,\alpha=\pi/180º \, rad)\)
i) Transformem el nombre de forma binòmica \((-8,0)\) a polars:
\(
r=\sqrt{-8)^2+(0)^2}=8\\
\alpha=\arctan {\frac{0} {-8}}=180º
\).
ii) Calculem el mòdul de les arrels:
\(
s=\sqrt[3]{|-8|} = 2
\).
iii) Calculem els angles:
\(
\beta=\frac{\alpha}{n}=\frac{180}{3}=60º \, (\frac{\pi}{3}):\\
\beta_{1}=\frac{\pi+2\pi*0}{3}=\frac{1\pi}{3}, \,\frac{180+360*0}{3}=60º\\
\beta_{2}=\frac{\pi+2\pi*1}{3}=\pi, \, \frac{180+360*1}{3}=180º\\
\beta_{3}=\frac{\pi+2\pi*2}{3}=\frac{5\pi}{3}, \, \frac{180+360*2}{3}=300º
\)
I les arrels són:
\(
2_{\pi/3}=\, 2_{60º}= \, 1 + i\sqrt{3}\\
2_{\pi}=\, 2_{180º}=\, -2\\
2_{\frac{5\pi}{3}}=\, 2_{300º}=\,1 – i\sqrt{3}
\)
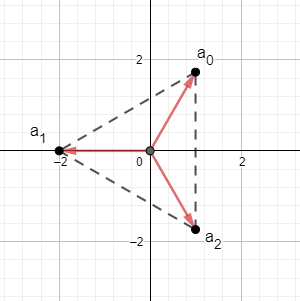
Si les representem, es forma un triangle regular (equilàter). Aquesta és una propietat general de les arrels, Les solucions formen polígons regulars de \(n\) costats:
Tens dubtes? Vols saber-ne més? T’agradaria que publiquéssim algun tema del teu interès? Has trobat algun error?
Envia’ns un comentari sense compromís i et respondrem tan aviat com ens sigui possible.