Arxiu d'etiquetes termodinàmica

Instruccions abans de començar

1. Introducció

La termodinàmica són les lleis de la conversió de l’energia i de l’energia en treball. Estudia la relació entre l’energia, la quantitat i direcció de la calor transferida i el treball en els processos físics i químics naturals.

Es basa en tres principis: 1) que l’energia de l’univers es manté constant i que es transforma per tal d’obtenir calor que es pugui transformar en treball, 2) que en un procés espontani l’entropia sempre augmenta i 3) que en el zero absolut l’entropia és zero.

Un sistema termodinàmic és una part de l’univers que imaginem isolada de la resta de l’univers en la qual es produeixen els processos termodinàmics. Diem que un sistema és obert quan hi ha bescanvi de matèria i energia amb l’exterior, tancat si el bescanvi és sols de matèria i aïllat quan no hi ha bescanvi ni d’energia ni de matèria.

Les variables termodinàmiques són les magnituds que determinen l’estat d’un sistema termodinàmic. Les variables termodinàmiques pressió, volum i temperatura són funcions d’estat (funció que defineix l’estat d’un sistema i que no depèn de com s’ha arribat a aquest estat). El valor d’una funció d’estat sols depèn de l’estat del sistema independentment del camí seguit per arribar-hi.

Els processos termodinàmics són les transformacions dels sistemes termodinàmics i de l’entorn:

• Procés isotèrmic: la temperatura es manté constant durant el procés.
• Procés isobàric: la pressió es manté constant durant el procés.
• Procés isocor: el volum es manté constant durant el procés.
• Procés adiabàtic: no hi ha bescanvi de calor entre el sistema i l’entorn.

La termodinàmica es fonamenta en quatre lleis, que són:

2. Llei zero de la termodinàmica:

Tres sistemes termodinàmics (A, B, C) es posen en contacte entre si:

Si A i B estan en equilibri termodinàmic i B i C estan en equilibri termodinàmic, A i C també estan en equilibri termodinàmic.

Quan dos sistemes en contacte no estan en equilibri termodinàmic, bescanvien energia o matèria.

3. Primer principi de la termodinàmica:

\[\Delta U=q+w\]

L’energia interna (ΔU) d’un sistema és l’energia cinètica i potencial dels àtoms i molècules d’aquest sistema. Si és un sistema aïllat, aquesta energia es conserva \[(ΔU=0)\] i sols pot variar si el sistema deixa de ser aïllat, és a dir, subministrant o cedint calor i treball.

L’energia interna és una funció d’estat. La calor i el treball no són funcions d’estat, és per això que es representen en minúscules. En un procés cíclic el sistema torna al seu estat original i, per tant, \[U_2=U_1, q=-w\].

Si el sistema absorbeix calor o rep treball (compressió), el signe és positiu perquè augmenta l’energia interna. Si desprèn calor o fa treball (expansió) el signe és negatiu perquè l’energia interna minva.

El bescanvi de calor es calcula fent \[q=m \cdot c_e \cdot \Delta T\]. En els canvis de fase, \[q=m \cdot \lambda\]. I el treball bescanviat entre el sistema i l’entorn és \[w=-P \cdot \Delta V\].

Segons els conveni de signes de la IUPAC, \[\Delta U=q+w\]. En aquest cas, la llei s’expressa en funció del treball termodinàmic fet per l’entorn sobre el sistema i \[w=-P \cdot \Delta V\]. Aquest conveni segueix les indicacions de Max Planck que considerava les aportacions al sistema positives i les aportacions a l’entorn negatives independentment de si el dispositiu termodinàmic genera (generador) o consumeix energia (motor).

Segons el conveni clàssic de Clausius, \[\Delta U=q-w\] i \[w=+P \cdot \Delta V\]. Ambdós sistemes són correctes, però s’ha de deixar clar quin es fa servir en cada moment per tal d’evitar confusions.

3.1 Procés isotèrmic (ΔT=0)

\[\Delta T=0 \rightarrow \Delta U=0 \rightarrow q=-w\]

Si la temperatura del focus calent i fred són iguals, l’energia interna dels àtoms i molècules no canvia i tot el calor rebut s’inverteix en fer treball.

En aquest procés, la calor és subministrada o retirada del sistema per tal de mantenir la temperatura constant.

3.2 Procés isobàric (ΔP=0)

\[
\Delta P=0 \rightarrow q=q_p, w=-P \cdot \Delta V \rightarrow \Delta U=q_p-P \cdot \Delta V
\\[0.5cm]
\text {Com que, } q_v=\Delta U \rightarrow q_p=q_v+P \cdot \Delta V
\\[0.5cm]
\text {Si en el procés intervenen gasos ideals }: q_p=q_v+ \Delta n \cdot R \cdot T
\\[0.5cm]
\Delta H=\Delta U+\Delta n \cdot R \cdot T
\\
q_p=q_v+\Delta n \cdot R \cdot T
\]

Com que en les reaccions que es fan al laboratori la pressió és constant, són processos isobàrics. A la calor \[(q_p)\] bescanviada en aquestes reaccions (a pressió constant) li diem entalpia \[(H)\]. L’entalpia pot ser positiva (reacció endotèrmica) o negativa (reacció exotèrmica). El sistema pot expandir-se o comprimir-se.

En un gas ideal, considerem que l’energia interna sols depèn de la temperatura perquè no es tenen en compte les interaccions entre els àtoms i molècules. Per tant, ja que \[\Delta P=\Delta V=0,\] sols fan moviments de translació (llei de Joule): \[w=0 \rightarrow \Delta U=q_v=m \cdot c_e \cdot \Delta T\].

3.3 Procés isocor (ΔV=0)

\[\Delta V=0 \rightarrow w=0, \Delta U=q_v=m \cdot c_e \cdot \Delta T\]

3.4 Procés adiabàtic (q=0)

\[q=0 \rightarrow \Delta U=w\]

El sistema no bescanvia calor amb el seu entorn. Un procés adiabàtic produeix un augment o descens de la temperatura del sistema. Si és reversible, és un procés isentròpic (l’entropia no varia) i \[d S=\frac{\delta q}{T}\].

En canvi, en un sistema isotèrmic, en el qual la transferència de calor és màxima, la temperatura ha de romandre constant.

4. Segon principi de la termodinàmica

La primera llei de la termodinàmica diu que l’energia es conserva, però hi ha molts processos en els quals es conserva l’energia que no són possibles (que un cos calent n’escalfi un de fred, per exemple).

La primera llei tampoc diu si la calor es pot convertir en treball o a l’inrevés ni en quina proporció, tot i que per experiència sabem que és possible transformar tota la calor en treball però no pas al revés.

La segona llei resol aquest problema i determina si un procés natural que compleixi la primera llei és possible o no.

4.1 Processos reversibles i processos irreversibles

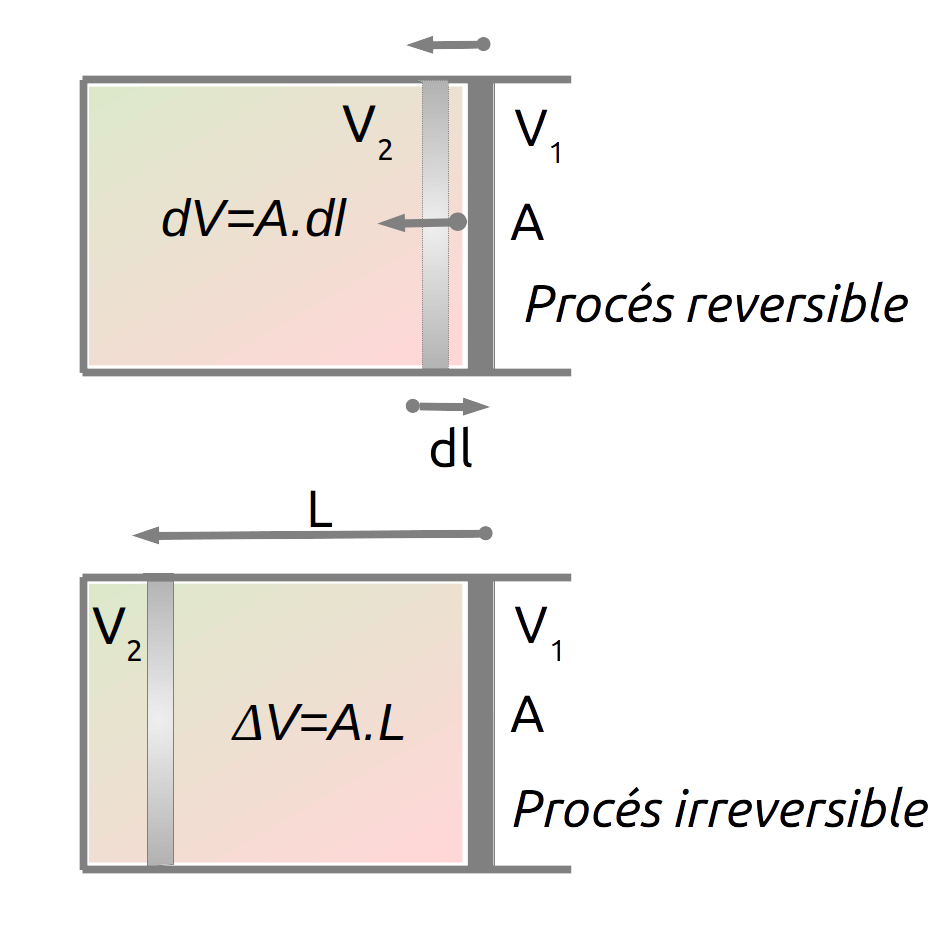
Imaginem un sistema termodinàmic en equilibri d’un gas en un èmbol a una pressió P1, temperatura T i que ocupa un volum V1, que canvia l’estat a una altra pressió P2 i volum V2:

• Un procés reversible és un procés en el qual les variables termodinàmiques que defineixen l’estat del sistema varien en quantitats infinitesimals, de manera que es pugui recuperar l’estat anterior invertint el procés. L’energia, treball o matèria bescanviada amb l’entorn també ha de recuperar-se quan s’inverteix el procés. En un procés reversible, el sistema passa per una successió continua d’estats en equilibri.
  
• Un procés irreversible és un procés que no pot recuperar l’estat anterior quan se n’inverteix el sentit.

A la pràctica, tots els processos naturals són irreversibles, però podem aproximar-los a processos teòrics reversibles per tal de estudiar-ne el comportament ideal. L’exemple anterior, és una compressió isotèrmica, però podria haver estat una compressió adiabàtica fent que no entrés ni sortís calor del sistema. En una compressió adiabàtica la temperatura del sistema augmentarà.

4.2 El Cicle de Carnot

Un cicle reversible important és el cicle de Carnot. El cicle de Carnot determina la capacitat màxima d’un sistema termodinàmic per a convertir la calor en treball. Per tant, determina el rendiment màxim teòric d’una màquina tèrmica reversible que opera entre una temperatura freda i una de calenta.

Però, les pèrdues d’energia d’un procés fan que la reversibilitat no sigui possible, i el rendiment d’una màquina tèrmica real sempre és més petit que el rendiment òptim d’una màquina de Carnot que funcioni amb el mateix interval de temperatures. El cicle de Carnot representa el màxim rendiment perquè tota la calor és subministrada al fluid del sistema a la màxima temperatura perquè no hi ha pèrdues.

El cicle de Carnot és el procés reversible d’un gas ideal de dues etapes isotèrmiques i dues d’adiabàtiques. Es representa en un diagrama P-V de quatre etapes:

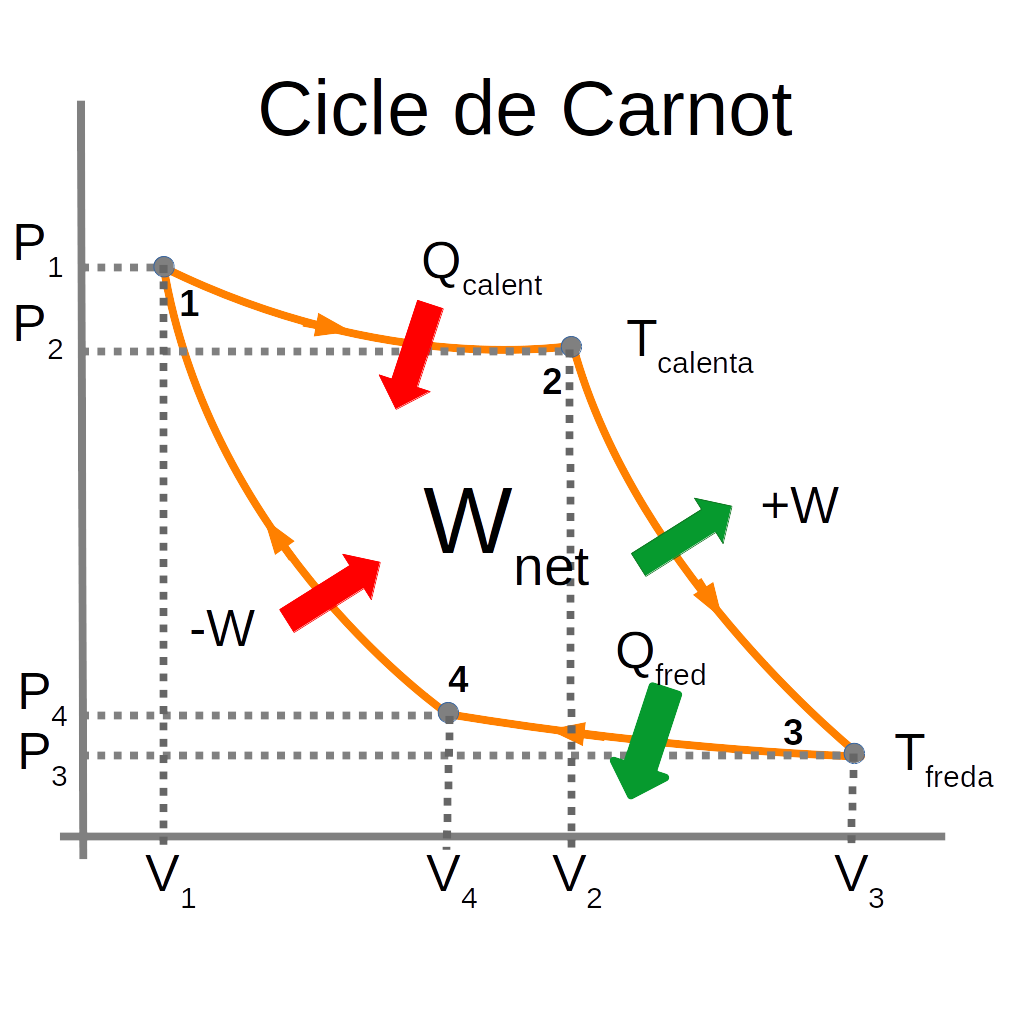
1-2 Expansió isotèrmica del gas ideal:

\[
\displaystyle{
P \cdot V=constant
\\
q_{calent}=w_{1-2}=n \cdot R \cdot T \cdot ln \frac {V_2} {V_1}
\\
dU=0
}
\]

En el pas 1-2 tota la calor absorbida es fa servir per expandir el gas.

2-3 Expansió adiabàtica del gas ideal:

\[
P \cdot V^\gamma=constant
\\
q_{2-3}=0
\\
w_{ 2-3 }=\Delta U=q_v=n \cdot C_v ( T_3-T_2 )
\]

El coeficient de dilatació adiabàtica, factor d’expansió isentròpica o índex adiabàtic, és la relació entre la capacitat calorífica o tèrmica a pressió constant i la capacitat calorífica a volum constant:

\[\displaystyle{\gamma= \frac {C_p} {C_v}}\]

En un gas ideal, la capacitat calorífica és constant amb la temperatura i

\[\displaystyle{H=C_p \cdot T , U=C_v \cdot T \rightarrow \gamma=\frac {H}{T}}\].

3-4 Compressió isotèrmica del gas ideal

\[
q_{fred}=w_{3-4}=n \cdot R \cdot T \cdot ln \frac{V_4} {V_3}
\\
dU=0
\]

En el pas 3-4 el treball de compressió fa que es cedeixi calor al focus fred.

4-1 Compressió adiabàtica del gas ideal

\[
P \cdot V^\gamma=constant
\\
q_{4-1}=0
\\
w_{ 4-1 }=\Delta U=q_v=n \cdot C_v ( T_1-T_4 )
\]

4.2.1 q, w, \[\Delta U\] i \[\eta\] globals

En les etapes isotèrmiques, \[\Delta U=0 \, i \, q=w\]. En les adiabàtiques, \[q=0\].

El rendiment és l’eficiència tèrmica de Carnot expressada en funció de les temperatures:

\[ \displaystyle {\eta=\frac{q_{fred}} {q_{calent}}}\]

L’eficiència tèrmica de Carnot expressada en funció de les temperatures és:

\[ \displaystyle {\eta=1-\frac{T_{calenta}}{T_{freda}}}\]

Com més gran sigui la diferència de temperatures d’operació més alta serà la eficiència màxima possible d’una màquina real operant amb la mateixa diferència de temperatures.

Si és una màquina irreversible real: \[\eta<\eta_C\]

Si és una màquina reversible teòrica: \[\eta=\eta_C\]

No és possible que \[η > η_C\]. L’eficiència tèrmica relativa d’una màquina és \[\displaystyle{\eta=\frac{\eta}{\eta_C}}\].

El diagrama TS de la màquina de Carnot és:

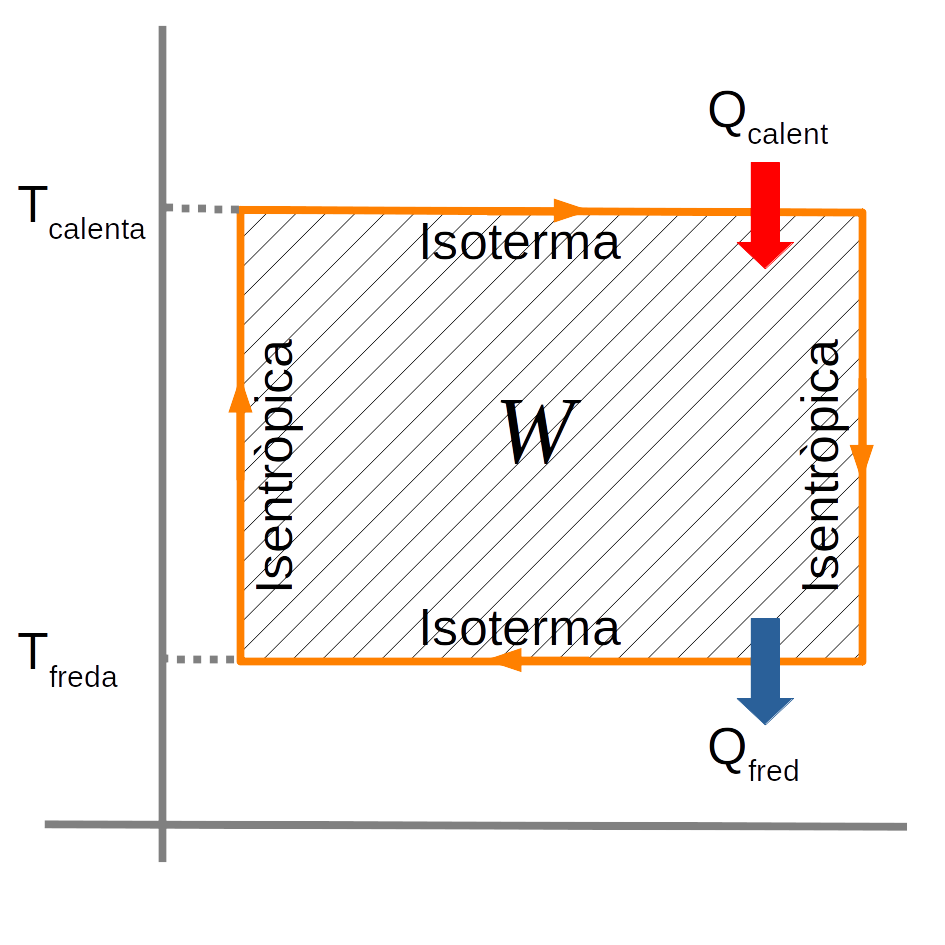
El treball fet en tot el cicle és:

\[W=T_{calenta} \cdot \Delta S_{1-2}-T_{freda} \cdot \Delta S_{3-4}=Q_{calenta}-Q_{fred}\] i la variació de l’entropia és zero.

En un sistema irreversible,

\[\Delta S=\Delta S_{calenta}- \Delta S_{freda} \rightarrow W=T_{freda} \cdot \Delta S\]

És a dir, que l’entropia de l’univers sempre augmenta. L’energia total es manté, però com que cada vegada és més freda, perd capacitat de fer treball.

4.3 La segona llei de la termodinàmica

El 1824 Carnot va adonar-se que la força motriu de les màquines de vapor era deguda al bescanvi de calor i la diferència de temperatures i que no tenia gens d’importància la substància de treball que s’emprés. Inventà el concepte de màquina i cicle reversibles i va afirmar que l’eficiència de les màquines reversibles que operen amb les mateixes temperatures és la mateixa, que cap màquina irreversible que funcioni amb aquestes temperatures pot superar l’eficiència de la màquina reversible, i que aquesta eficiència és la màxima que pot assolir qualsevol màquina tèrmica que funcioni amb aquestes temperatures.

Després de la mort de Carnot el 1832, Clàusius, Kelvin i Planck confirmaren aquest principi i van enunciar la segona llei de maneres diferents. Però aquests enunciats són tots equivalents i demostren que sols és possible que la calor flueixi de la font calenta a la freda espontàniament, i que per fer el procés invers cal subministrar treball al sistema.

4.4 L’entropia

La llei zero de la termodinàmica es relaciona amb la temperatura. La primera, es relaciona amb l’energia interna. I la segona es relaciona amb l’entropia.

L’entropia es definí inicialment com l’energia no disponible per fer treball. Més tard, Ludwig Boltzmann definí l’entropia com la probabilitat de les possibles configuracions microscòpiques dels àtoms i molècules que es corresponen amb un estat macroscòpic del sistema i demostrà que \[S=k*\ln\Omega.\]

4.4.1 Processos reversibles

En el cicle de Carnot, \[\displaystyle{\frac{ Q_1 } { T_1 }=\frac{ Q_2 } { T_2 }, \frac { Q_1 } { T_1 }-\frac{ Q_2 } { T_2 }=0.}\]

L’entropia \[S\] és defineix com \[\displaystyle{dS=\frac{\delta q}{dT}.}\] \[S\] també és una funció d’estat.

4.4.2 Processos irreversibles

Com que és una variable d’estat, l’entropia sols depèn de l’estat del sistema. En un procés irreversible el canvi d’entropia entre dos estats en equilibri augmenta:

Exemple: dilatació lliure

Una expansió isotèrmica lliure d’un gas ideal és un procés irreversible. Calcularem el canvi d’entropia emprant la trajectòria reversible de l’etapa 1-2 del cicle de Carnot:

\[
\displaystyle{
S_2-S_1=\int_{1}^{2} {\frac{ dQ } { T }}=n \cdot R \cdot ln \frac{ V_2 } { V_1 }
\\[0.5cm]
\text{Si suposem que en l’expansió es dobla el volum:}
\\[0.5cm]
\Delta S=n \cdot R \cdot \ln2>0
}
\]

Exemple: conducció de la calor

Dos cossos semblants que tinguin temperatures diferents (T1, T2) arribaran a una temperatura d’equilibri Te. Com en l’exemple anterior, per a calcular el canvi d’entropia cercarem un procés reversible de T1 a T2:

El procés irreversible i el procés reversible usat per a calcular el canvi d’entropia són dos processos diferents, però com que els estats inicial i final d’ambdós coincideixen i l’entropia és una funció que depèn sols de l ‘estat del sistema, podem usar el reversible per a calcular en canvi d’entropia de l’irreversible.

\[
\displaystyle{
\text{L’entropia perduda pel cos calent és: } \Delta S_1 \simeq -\frac{ Q } { T_{1m} }
\\
\text{I l’entropia guanyada pel cos fred és: } \Delta S_2 \simeq +\frac{ Q } { T_{2m} }
\\
T_{1m} \text{ és la temperatura mitjana de } T_1,T_e \text{ i } T_{2m} \text{ és la temperatura mitjana de } T_2, T_e.
\\
\text{Q és el calor extret de } T_1 \text{ que suposem es transfereix totalment a } T_2.
\\[0.5cm]
\text{Per tant, el canvi d’entropia del procés és:}
\\[0.5cm]
\Delta S=\Delta S_1+\Delta S_2=-\frac{ Q }{ T_{1m} }+\frac{ Q }{ T_{2m} }
\\[0.5cm]
\text{Com que } T_{1m}>T_{2m}, S_2>S_1 \text{ i l’entropia del sistema augmenta.}
}
\]

4.5 Entropia i la segona llei

En un procés natural o irreversible que comença i acaba en dos estats d’equilibri diferents sempre anirà en la direcció que faci créixer l’entropia de l’univers (sistema + medi ambient).

Però, en un sistema reversible, l’entropia de l’univers no varia perquè, si augmenta l’entropia del sistema, minvarà la de l’entorn, i si minva la del sistema, augmentarà la del medi ambient. La raó és que la diferència de temperatura entre el sistema i el medi ambient tan sols és dt, mentre que en un d’irreversible la diferència de temperatura entre ambdós sistemes és molt gran.

En els processos adiabàtics, reversible o irreversibles, no hi ha transferència de calor amb el medi ambient (entorn). Per tant, el canvi d’entropia és el canvi d’entropia del sistema termodinàmic \[(ΔS_{univers}=ΔS_{sistema}+ΔS_{medi ambient}).\]

Exemple

Calculeu el canvi d’entropia d’un sistema d’1 Kg de gel a 0ºC que es fon irreversiblement en aigua a la mateixa temperatura. La calor latent de fusió es de 79.6 cal/g:

\[
\displaystyle{
\text{En un procés reversible:}
\\[0.5cm]
S_{aigua}-S_{gel}=\int_{0}^{Q̣}{\frac{ dQ }{ T }}=\frac{ 1 }{ T } \int_{0}^{Q}{dQ}=\frac{ Q }{ T }
\\
1.10^3 g \cdot 79.6 cal/g=7.96.10^4 cal \rightarrow \frac{ Q }{ T }= \frac{ 7.96.10^4}{ 273 }=292 cal/K= 1 220 J/K.
}
\]

Exemple

Calculeu el canvi d’entropia d’un gas ideal en una dilatació isotèrmica reversible de V1 a V2:

\[
\displaystyle{
dU=\delta q-P \cdot dV=0, \delta q=p \cdot dV
\\
dS=\frac{ \delta q }{ T }=\frac{ P. dV }{ T }
\\
\text{Com que }p=\frac{nRT}{V} \rightarrow dS= \frac{n \cdot R \cdot dV } { V }
\\
S_2 – S_1=\int_{V_1}^{V_2} {dS}=\int_{V_1}^{V_2} {\frac{n \cdot R \cdot dV }{ V }}= \mathbf{n \cdot R \cdot [ln { V }] _{V_1}^{ V_2 }}
}
\]

Com que és un procés reversible, l’entropia del sistema més l’entorn no varia: es subministra calor al gas per tal que s’expandeixi, que després és cedeix a l’entorn.

5. Tercer principi de la termodinàmica

La tercera llei de la termodinàmica proporciona una escala absoluta de valors per a l’entropia. La variació d’entropia d’un sòlid cristal·lí al zero absolut és zero.

6. Energia lliure de Gibbs

Segons la primera llei de la termodinàmica, \[ΔU=q+w \]. \[w \] és la suma del treball d’expansió més el treball útil: \[ΔU=q+w_e+w_{útil}=q-pΔV+w_{útil} \].

Si el procés és reversible,

\[q=TΔS \rightarrow ΔU=TΔS-pΔV+w_{útil}, w_{útil}= ΔU-TΔS+pΔV \].

En un procés a pressió constant:

\[H=U+pΔV \rightarrow w_{útil}= ΔU-TΔS+pΔV=ΔH-TΔS, ΔG= ΔH-TΔS \].

\[ΔG \] és la variació d’energia lliure de Gibbs o el màxim treball útil que es pot obtenir a temperatura i pressió constant en un procés reversible. És una funció d’estat que prediu la direcció de l’equilibri (mecànic i tèrmic) i d’espontaneïtat d’una reacció química en un sistema tancant a \[P , T \] constants, on sols és possible treball \[P-V \].

Els canvis en l’energia de Gibbs són útils per a avaluar el màxim treball útil que es pot obtenir a partir de processos termodinàmics. El valor de la funció energia de Gibbs és mínima quan el sistema assoleix l’equilibri. Si \[ ΔG>0 \], el procés no serà espontani.

Demostració:

Segons la segona llei de la termodinàmica:

\[ΔS_{univers}=ΔS_{sistema termodinàmic}+ΔS_{medi ambient}\].

Si el sistema està en equilibri tèrmic amb l’entorn:

\[
\displaystyle{
ΔS_{medi ambient}=ΔH_{medi ambient}/T=\frac{+ΔH_{sistema termodinàmic}} {T}
\\[0.5cm]
ΔS_{univers}=ΔS_{sistema termodinàmic}-\frac{+ΔH_{sistema termodinàmic}} {T}
\\
T \cdot ΔS_{univers}=T \cdot ΔS_{sistema termodinàmic}-ΔH_{sistema termodinàmic}
\\[0.5cm]
\text{Com que en un procés espontani } ΔS_{univers} \gt 0:
\\[0.5cm]
T \cdot ΔS_{sistema termodinàmic}-ΔH_{sistema termodinàmic}>0
\\
-(ΔH_{sistema termodinàmic}-T \cdot ΔS_{sistema termodinàmic}>0,
\\
-ΔG \gt 0 \rightarrow ΔG \lt 0.
}
\]

• \[\Delta G\]<0 si el procés és espontani
• \[\Delta G\]> 0 si el procés no és espontani (per tant, el procés invers serà espontani).
• \[\Delta G\]= 0 si el sistema és en equilibri químic.

Exercicis PAU