La matèria

Instruccions abans de començar

Introducció

La matèria són les coses que formen la realitat que percebem mitjançat els sentits. Són els objectes detectables i mesurables per mitjans físics que ocupen un lloc a l’espai i tenen energia. La matèria experimenta canvis en el temps.

Substància és la matèria de què estan formats els cossos. Es distingeixen entre elles per les propietats físiques, químiques i organolèptiques.

L’organització de la matèria que forma el nostre univers físic és:

1. Estructura atòmica

1.1 L’àtom

La matèria és feta d’àtoms. L’àtom té un nucli fet de protons (\[p^+\]) i neutrons (\[n^0\]) i una escorça per on orbiten els electrons (\[e^-\]).

Tots els àtoms són neutres elèctricament (tenen tants protons com electrons), però com que no tenen la darrera capa d’electrons (capa de valència) del tot plena, són inestables. Per aconseguir omplir la capa de valència, reaccionen amb altres elements i formen compostos. Els gasos nobles no reaccionen amb cap altre àtom perquè tenen la capa de valència del tot plena, és per això són monoatòmics.

Quan un àtom perd electrons o guanya electrons es transforma en un ió. Si els perd, resta amb càrrega positiva (ara té més protons que electrons) i diem que és un ió positiu o un catió. Si els guanya, resta amb càrrega negativa (té més electrons que protons) i diem que és un ió negatiu o un anió.

Una unitat de massa atòmica (u.m.a) són \[1,62.10^{-27 }Kg\], aproximandament la massa d’un protó o d’un neutró. Segons aquesta definició, la massa atòmica d’un àtom expressada en u.m.a (A) és el nombre de protons (Z) més el nombre de neutrons (N): A=Z+N.

\[1 u.m.a=1,62.10^{-27 }Kg\]

Per tant, podem saber el nombre de neutrons que té un àtom fent la diferència del nombre màssic (A) i el nombre de protons (Z) que ens indica la taula periòdica: N=A-Z. L’hidrogen és l’únic element de la taula periòdica que no té cap neutró.

Exemple:

\[
\mathbf{{}^{12}_{6}C}
\\
A=12
\\
Z=6
\\
N=12-6=6
\]

Si un àtom té un nombre de neutrons diferent de A-Z, diem que és un isòtop d’aquest element. Molts elements de la taula periòdica tenen isòtops i, de fet, el nombre màssic A d’un element és la massa atòmica ponderada de la massa de tots els isòtops d’aquest element.

\[
\displaystyle{\bar M=\frac{ \Sigma (\text{% abundància} \cdot M_a) }{100 }}
\]

Exemple:

\[\displaystyle{
Li-6: \textbf{7.59%}, M_a=6.015
\\
Li-7: \textbf{92.41%}, M_a=7.016
\\
\overline M_{Li}=\frac{\text{7.59%} \cdot 6.015+ \text{92.41%} \cdot 7.016 }{ 100 }=\mathbf{6.94 g.mol^{-1}}
\\( M_a \text { del liti que mostra la taula periódica )}
}
\]

1.2 Elements

Un element és la matèria de què estan formats els cossos amb propietats físiques i químiques que no es pot dividir en parts més petites. Estan classificats a la taula periòdica.

Un mol és la quantitat de substància que té \[6,023.10^{23}\] partícules (subatòmiques, atòmiques o moleculars).

Exemple:

\[\text{1 mol } H_2 =6,023.10^{23} molècules \, H_ 2
\\
\text{1 mol } Fe=6,023.10^{23} àtoms \, Fe
\\
\text{1 mol } e^-=6,023.10^{23} \, e^- …
\]

La massa atòmica d’un element és la massa d’un mol d’àtoms d’aquest element. És relativa a la massa atòmica de \[C^{12}\], el patró de referència. La trobem a la taula periòdica per a cada element.

Exemple:

\[
M_A (H)= 1,008 g.mol^{-1}
\\
M_A (O)=15,999 g.mol^{-1}…
\]

1.3 Molècules

Una molècula és una agrupació d’àtoms units per un enllaç covalent (compartició d’electrons entre dos àtoms). Els àtoms units per enllaços iònics (enllaç electroestàtic entre un anió un catió) formen xarxes cristal·lines. Una molècula és una substància pura composta.

La massa molecular d’una molècula és la suma de les masses atòmiques que formen la molècula.

Exemple:

\[M(H_2SO_4)= 2.1,008+1.32,064+4.15,999=98,076 \, g.mol^{-1}\]

La fórmula molecular d’un compost representa la naturalesa i el nombre d’àtoms que formen el compost. Per exemple, la molècula d’àcid sulfúric (\[H_2SO_4\]) conté dos àtoms d’hidrogen, un de sofre i quatre d’oxigen.

1.4 Model atòmic de Dalton

Teoria sobre la constitució de la matèria (John Dalton, 1808) segons la qual la matèria està feta d’àtoms indivisibles i immutables. Aquesta teoria justifica les relacions ponderals senzilles entre els composts químics:

• Els elements químics estan constituïts per partícules discretes, diminutes i indivisibles, anomenades àtoms que romanen inalterables en qualsevol procés químic.
• Els àtoms d’un mateix element són tots iguals en massa, mida i en qualsevol altra propietat física o química.
• Els compostos químics estan formats per “àtoms de compost” (molècules), tots iguals entre si, és a dir, quan dos o més àtoms de diferents elements es combinen per formar un mateix compost ho fan sempre en proporcions de massa senzilles, definides i constants.
• A les reaccions químiques, els àtoms ni es creen ni es destrueixen, només canvien la seva distribució.

Per a Dalton, les partícules dels elements gasosos estaven constituïdes per un sol àtom (H, O, CI, N…) i les dels compostos com l’aigua o el clorur d’hidrogen estaven formades per sols dos àtoms diferents (HO, ClH).

Això no podia explicar la llei dels volums de combinació de Gay-Lussac segons la qual «hi ha una relació senzilla de nombres enters entre els volums dels gasos d’una reacció química».

Exemple:

\[
2H_2+1O_2 \rightarrow 2H_2O
\\
1H_2+1Cl_2 \rightarrow 2HCl
\]

1.5 Les hipòtesis d’Avogadro

1. Igual volum de gasos, en les mateixes condicions de temperatura i pressió, contenen el mateix nombre de molècules.
2. Els elements gasosos, com ara hidrogen, nitrogen i oxigen, estan constituïts per molècules diatòmiques que, en una reacció química, es poden separar en dos àtoms.

Segons Avogadro:

Les molècules són molt petites comparades amb l’espai que les separa en els gasos.

En una reacció química una molècula de reactiu reacciona amb una o més molècules d’un altre produint una o més molècules de producte.

Una molècula no pot reaccionar amb un nombre no sencer de molècules, perquè la unitat mínima de reactiu és la molècula.

Per tant, hi ha d’haver una relació directa entre els volums i el nombre de molècules dels gasos:

Això justificà la llei de la combinació de volums de Gay-Lussac.

1.6 Compostos

Són substàncies pures que es poden descompondre en els seus elements emprant processos químics. Els diferents elements es combinen en proporcions fixes. Les propietats dels compostos són diferents de les propietats dels elements que els formen. Es representen amb fórmules químiques (\[H_2SO_4, H_2O, SO_3…\]).

Exemple:

L’àcid sulfúric, l’aigua, la sal de cuina…

1.6.1 Composició centesimal

La composició centesimal d’un compost és el tant per cent en massa que hi ha de cadascun dels elements que el formen. És una característica de cadascun.

La fórmula empírica indica la naturalesa i proporció dels elements del compost. La fórmula molecular indica el nombre d’àtoms que hi ha de cada element.

Es pot calcular, o bé (1) la fórmula empírica i molecular d’un compost a partir de la composició centesimal, o bé (2) la composició centesimal a partir de la fórmula molecular

Per a calcular la fórmula molecular a partir de l’empírica ens cal la massa molecular del compost.

Exemple:

(1) Per a calcular la fórmula molecular a partir de la composició centesimal:

La composició centesimal d’un compost que té una massa molecular de 140 g/mol és: 51,42 % de C, 40 % de N; 8,57 % de H. Trobeu-me la fórmula molecular.

\[
\displaystyle{
\\[0.5cm]
\text{1. La massa de cada element en 100g del compost és:}
\\
C: 51,42 g
\\
N: 40 g
\\
H: 8,57 g
\\[0.5cm]
\text{2. Els mols de cada element són:}
\\[0.5cm]
C: 51,42 g~C \cdot \frac{1 mol~C} {~12g~C}=4,29 \text{ mols C}
\\
N: 40 g ~N \cdot \frac{~1 mol~N} {~14g~N}=2,86 \text{ mols N}
\\
H: 8,57 g \cdot \frac{~1 mol~H} {~1g~H}=8,57 \text{ mols H}
\\[0.5cm]
\text{3.Trobem la relació molar de cada component del compost dividint}
\\
\text{ pel nombre més petit de mols (2,86):}
\\[0.5cm]
C: \frac{ 4,29 } { 2,86 }=1,5 \enspace
N: \frac{ 2,86 } { 2,86 }=1 \enspace
H: \frac{ 8,57 } { 2,86 }=3
\\[0.5cm]
\text{4.Per tant, la fòrmula empírica i el pes-fórmula és:}
\\[0.5cm]
C_3 N_2 H_6 \rightarrow M_{fórmula} =12 \cdot 3+2 \cdot 14+6 \cdot 1=70g
\\[0.5cm]
\text{5. I la fórmula molecular és:}
\\[0.5cm]
\frac{\text{pes-fórmula molecular}}{\text{pes-fórmula empírica}}=\frac{ 140g } { 70g }=2
\\[1cm]
\mathbf {Fórmula \, molecular: C_6 N_4 H_{12}}
}
\]

(2) Per a calcular la composició centesimal a partir de la fórmula molecular, usarem l’expressió:

\[
\displaystyle
{
\%C=n_ {element} \cdot {\frac{M_{element}} {M_{compost}}} \cdot 100
}
\]

Exemple:

\[
\displaystyle
{
\text{Si la fórmula molecular del compost és } C_6 N_4 H_{12}:
\\[0.5cm]
\text{1. Primer calculem la massa molecular del compost:}
\\
M=6.12+4.14+12.1=140 ~g/mol
\\[0.5cm]
\text{2. Després calculem la composició centesimal de cada element:}
\\[0.5cm]
\%C= {\frac {6 \cdot 12 ~g/mol } { 140 ~g/mol }} \cdot 100= \mathbf{51,43\%}
\\
\%N= {\frac {4 \cdot 14 ~g/mol } { 140 ~g/mol }} \cdot 100= \mathbf{40\%}
\\
\%H= {\frac {12 \cdot 1 ~g/mol } { 140 ~g/mol }} \cdot 100= \mathbf{8,57\%}
}
\]

2. Mescles i barreges

Una mescla o barreja és una combinació de substàncies pures. Cada component d’una mescla o barreja conserva les seves propietats físiques i químiques i es poden separar per mètodes físics.

Exemple:

Aigua amb sal, l’aire, aigua i oli, aigua i esperit de vi, els aliatges…

(Vegeu Mescles i barreges per a saber-ne més).

3. Reaccions químiques i estequiometria

3.1 Reaccions químiques

Una reacció química és el canvi o transformació d’un o més elements químics o compostos (reactius) per a formar altres elements químics o compostos amb propietats diferents (productes).

En una reacció química és trenquen i es reorganitzen els enllaços dels reactius originant els productes. Les reaccions químiques s’expressen mitjançat una equació química. Si la reacció desprèn energia, diem que és exotèrmica. Si li hem de donar energia per tal que es produeixi, diem que és endotèrmica.

Exemple:

\[
H_2 S O_4+2NaOH~ ⇌ ~Na_2 SO_4+2H_2 O
\\
C_6 H_{12} O_6+6O_2~ ⇌ ~6CO_2 + 6H_2 O
\]

3.2 Llei conservació de la massa

La massa dels productes d’una reacció química és igual a la massa dels reactius de la reacció (Antoine L. Lavoisier, 1785).

3.3 Lleis ponderals

Conjunt de lleis relatives al pes que constitueixen el fonament de l’estequiometria.

La formulació de les lleis ponderals arrenca, històricament, del principi de la conservació de la matèria de Lavoisier:

3.3.1 Llei de les proporcions recíproques o equivalents

Els pesos de dos elements (o bé múltiples simples d’aquests pesos) que reaccionen amb el mateix pes d’un tercer element poden també reaccionar entre ells (Jeremies Benjamin Richter, 1792).

Exemple:

\[
\displaystyle
{
Substància 1 (Cl_2 O): \frac{2×35.45} {16}=4,431
\\
Substància 2(P_2 O_3): \frac{2×30.97} {3×16}=1,290
\\
\text{Relació entre el pes del clorur i del fòsfor}: \frac{ 4.431 } { 1.290 }=\mathbf {3.435}
\\
Substància 3 (PCl_3): \frac{3×35.45} {1×30.97}=\frac{ 106.35 } { 30.97 }=\mathbf {3.434}
}
\]

3.3.2 Llei de les proporcions definides o constants

Dos o més elements que es combinen per formar un compost ho fan sempre en la mateixa proporció (Louis Joseph Proust, 1799).

Exemple:

\[
\displaystyle
{
H_2 O \rightarrow \frac{ 2 \, g \, d’hidrògen } { 16 \, g \, d’oxígen }= \mathbf{\frac{1} {8}}
}
\]

3.3.3 Llei de les proporcions múltiples

Si dos elements es combinen per formar més d’un compost, els pesos d’un dels elements que es combinen amb el mateix pes de l’altre estan en la relació de nombres enters simples (John Dalton, 1803).

Exemple:

\[
\displaystyle
{
Cu O \rightarrow \frac{ 1×63.55 \, g \, de \, coure} {16 \, g \, d’oxígen }
\\
Cu_2 O \rightarrow \frac{ 2×63.55 \, g \, de \, coure} {16 \, g \, d’oxígen }
}
\]

Per tant, la relació de les masses de coure és 1:2.

3.4 Estequiometria

L’estequiometria és la branca de la química que estudia les relacions numèriques dels reactius i productes en una reacció química.

Exemple:

En la reacció de combustió de la glucosa, totes les relacions estequiomètriques dels reactius i productes són:

\[
\displaystyle
{
C_6 H_{12} O_6+6O_2 ⇌ 6CO_2 + 6H_2 O
\\[0.5cm]
\frac{ 1 mol \, C_6 H_{12} O_6 } { 6 mols \, O_2 }, \frac{ 1 mol \, C_6 H_{12} O_6 } { 6 mols \, CO_2 }, \frac{ 1 mol \, C_6 H_{12} O_6 } { 6 mols \, H_2 O }
\\
\frac{ 6 mols \, O_2 } { 6 mols \, CO_2 }=\frac{ 1 mols \, O_2 } { 1 mols \, CO_2 }, \frac{ 6 mols \, O_2 } { 6 mols \, H_2 O }=\frac{ 1 mols \, O_2 } { 1 mols \, H_2 O }
\\
\frac{ 6 mols \, CO_2 } { 6 mols \, H_2 O }=\frac{ 1 mols \, CO_2 } { 1 mols \,H_2 O }
}
\]

Les relacions inverses també són possibles.

3.5 Càlculs

Per a calcular les diferents quantitats que reaccionen o es formen en una reacció química, a més de l’estequiometria de la reacció ens caldrà saber la densitat i la massa atòmica o molecular d’algun dels components de la reacció.

Si algun dels components és gasós, haurem de fer servir la llei dels gasos ideals per a saber quants mols reaccionen o es produeixen. També hem d’entendre l’ús dels factors de conversió.

Exemples:

\[
\displaystyle
{
C_6 H_{12} O_6 +6O_2 \rightarrow 6CO_2+6H_2 O
\\
M_A( C )=12.001 \,g.mol^{-1}, \,M_A( H )=1.008 \,g.mol^{-1}, \,M_A( O )=15.999 \,g.mol^{-1}, \\
M(C_6 H_{12} O_6 )=180.096g
\\[0.5cm]
\textbf{1. Relacions estequiomètriques}
\\[0.5cm]
\textbf{a. Quants grams d’} H_2 O \textbf{ produiran 50g de glucosa?}
\\
50g \,glucosa \cdot { \frac{mol \, glucosa } { 180.096g \, glucosa } } \cdot { \frac{6 mols \, H_2 O } { 1 mol \, glucosa } } \cdot { \frac{18g \, H_2 O } { 1 mol \, H_2 O} }= \textbf{29.841 g } H_2 O
\\[0.5cm]
\textbf{b. Quants litres de } CO_2 \text{ produiran 100c.c d’oxígen en c.n?}
\\
100cm³ \, O_2 \cdot {\frac{1L} {1 000cm³}} \cdot { \frac{1 mol \, O_2} {22.386 L }} \cdot { \frac{6 mols \, CO_2} {6 mols \, O_2} } \cdot { \frac{22.386L} {1 mol} }=\mathbf{0.1 mols \, CO_2}
\\[0.5cm]
\textbf{c. Amb quantes molècules d’oxigen reaccionaran 25g de glucosa?}
\\
25g \, glucosa \cdot { \frac{1 mol \, glucosa } { 180.096g \, glucosa }} \cdot { \frac{ 6 mols \, O_2} { 1 mol \, glucosa} } \cdot { \frac{6.023×10^{23} \, molècules} {1 mol}}
\\
=\mathbf{5.016×10^{23} \, molècules \, O_2}
\\[0.5cm]
\textbf{2. Amb reactiu limitant}
\\[0.5cm]
\textbf{a. Quants grams d’ aigua produiran 50g de glucosa i 50g d’oxígen?}
\\
50g \, glucosa \cdot { \frac{1 mol \, glucosa } { 180.096 g \, glucosa }}=0.278 mols \, glucosa
\\
50g \, O_2 \cdot {\frac {1 mol \, O_2 }{ 15.999g \, O_2 }}=3.
125 \, mols O_2
\\
\frac{ 1 mol \, glucosa }{ 6 mols \, O_2 }=\frac{ 0.278 mols \, glucosa }{x \,mols \, O_2 } \rightarrow x=1.668 mols \, O_2 < 3.125 \, mols O_2
\\
\textbf{Per tant, el reactiu limitant és la glucosa}.
\\
0.278 \, mols \, glucosa \cdot {\frac{6H_2O}{1glucosa}}=1.668 \, mols \, d’H_2O
\\
1.668 \, mols \, d’H_2O \cdot {\frac{18 \, g \, H_2O}{1 \, mol \, d’H_2O}}=\mathbf{30.024 \, g \,d’H_2O}
\\[0.5cm]
\textbf{3. Amb rendiment de la reacció}
\\
\textbf{Si el rendiment de la reacció és del 67%, quan grams d’aigua es produiran?}
\\
1.668 \, O_2 \cdot { \frac{1mols \, H_2 O} {1 mols \, O_2} } \cdot { \frac{18.015 g \, H_2 O } {1 mol \, H_2 O} } \cdot67\%=\mathbf{20.133 g \, H_2 O}
\\[0.5cm]
\textbf{4. Amb puresa dels reactius}
\\[0.5cm]
\textbf{10 g de mineral de zinc del 60% de puresa reacciona amb}
\\
\textbf{20ml d’àcid sulfúric 98.6% i densitat 1.823g/ml.}
\\
\textbf{Determinar el volum d’hidrogen produït a 25ºC i 740mmHg.}
\\
Zn⁰ + H_2 S O_4 \rightarrow Zn( SO_4)+H_{2_(g) }
\\
60\% \,10g Zn \cdot { \frac{ mol \, Zn } { 65.38 g \, Zn } } \cdot { \frac{1 mol \, H_2 } { 1 mol \, Zn } }=0.0918 mols \, H_2
\\
V=\frac{ n \cdot R \cdot T }{ P }=\frac{ 0.0918 \cdot 0.082 \cdot (273+25) }{ 740mmHg \cdot {\frac{1 atm }{ 760mmHg}}} =\textbf{ 2.303 L.}
}
\]

4. Formes d’agregació de la matèria

4.1 Estat sòlid

Estat de la matèria en què les molècules que la componen, a causa de les forces de cohesió, tenen un moviment molt restringit, limitat a una vibració entorn d’una posició d’equilibri fixa.

Els sòlids poden classificar-se en amorfs i cristal·lins, en funció de si presenten una estructura regular en la disposició de les partícules que els componen. En els polímers coexisteixen estructures regulars i cristal·lines amb zones que presenten una estructura irregular, amorfa.

L’estructura d’un sòlid té un paper fonamental en les seves propietats. Per exemple, el grafit pur i el diamant són formats per àtoms de carboni i només es diferencien per la xarxa cristal·lina.

Els sòlids cristal·lins tenen un punt de fusió ben definit i presenten comportaments diferents segons la direcció en la qual fem la mesura.

En presència d’un solvent molt polar com l’aigua, produeixen solucions amb ions en la fase líquida, de manera que la solució és conductora del corrent elèctric. Els sòlids amorfs no són solubles en els solvents comuns.

Classes de sòlids: metalls, polímers, materials ceràmics, compostos, biomaterials i semiconductors.

Les propietats físiques del sòlids són: elèctriques, òptiques, fotovoltaiques, dielèctriques, mecàniques, termomecàniques, electromecàniques i termoelèctriques.

Les lleis que estudien els sòlids són la conservació de la massa, la conservació de la quantitat de moviment, la conservació de l’energia i l’entropia.

La física de l’estat sòlid estudia les propietats físiques dels materials sòlids utilitzant disciplines tals com la mecànica quàntica, la cristal·lografia, l’electromagnetisme i la metal·lúrgia física. La física de l’estat sòlid forma la base teòrica de la ciència de materials.

La mecànica dels sòlids és la branca de la física que estudia el comportament dels sòlids. Es divideix en:

Mecànica de sòlids rígids: estudia el moviment i l’equilibri mecànic.

Mecànica del sòlids deformables: n’estudia el comportament ( la tensió, la deformació, l’elasticitat, la plasticitat i la flexió) quan les forces i canvis exteriors el deformen.

4.2 Estat líquid

L’estat líquid és l’estat de la matèria en el qual les molècules resten relativament lliures i poden canviar llur posició respectiva, però les forces de cohesió les obliguen a mantenir-se en un volum fix.

Com els sòlids, els líquids són pràcticament incompressibles, però s’adapten a la forma del recipient que els conté.

En el Sistema Internacional, la unitat de capacitat és el litre. La unitat per a mesurar el volum dels sòlids i grans volums de líquids és el m³.

Les característiques macroscòpiques dels líquid són: la viscositat, la tensió superficial, la untuositat i la capil·laritat.

Les propietats òptiques, elèctriques i calorífiques dels líquids són: la transparència, l’índex de refracció, la conductivitat elèctrica, la capacitat dielèctrica i la conductivitat tèrmica.

La mecànica de fluids formada per la hidroestàtica (principi de Pascal i principi d’Arquimedes) i la hidrodinàmica estudia l’efecte de les forces sobre els fluids (líquids i gasos) i el seu moviment.

4.3 Estat gasós

Estat de la matèria en què les molècules que el componen resten poc lligades entre elles per les forces de cohesió. No presenta ni una forma ni un volum definits, sinó que sempre omple totalment i uniformement el recipient que el conté.

Les propietats físiques macroscòpiques d’un gas són: la pressió, la temperatura, el volum específic i la densitat.

La teoria cinètica molecular estudia el comportament microscòpic dels gasos i permet explicar-ne el comportament macroscòpic.

El moviment de les molècules i els àtoms determina la temperatura del sistema. En augmentar la temperatura, també augmenta el moviment lineal, rotacional o vibratori dels àtoms i molècules d’un gas. En canvi, en els sòlids sols fa augmentar la vibració de les molècules atès que l’estructura cristal·lina evita els moviments lineals o rotatoris.

El moviment brownià és un model matemàtic que s’utilitza per descriure el moviment aleatori de les partícules immerses a un fluid.

Les atraccions o repulsions entre les partícules d’un gas (forces intermoleculars de Van der Waals) són importants per a la determinació de les propietats físiques del gas.

Les característiques dels gasos són:

• Baixa densitat i viscositat relatives comparades amb els estats sòlid i líquid.
• Són compressible, a diferència dels sòlids i líquids.
• Es difonen amb facilitat.

(La difusió molecular és el transport de matèria produït pel moviment molecular a l’atzar. Es dóna en tots els estats de la matèria, bé que el procés és molt més lent en sòlids que en líquids o gasos -difusió gasosa. El resultat final és sempre el transport de matèria d’un lloc on la concentració és més elevada en un altre on no ho és tant, fins a arribar a una igualtat de concentracions.)

La solubilitat d’un gas en un líquid minva amb la temperatura.

4.3.1 Les lleis dels gasos

4.3.1.1 Llei de Dalton dels gasos (o de les pressions parcials)

La pressió que fa una barreja de gasos és igual a la suma de les pressions parcials que fa individualment cadascun dels gasos:

\[\Sigma p_i=P\]

La pressió parcial d’un gas és la pressió que faria si ocupés tot sol el volum de la barreja a la mateixa temperatura:

\[\displaystyle {p_i=\frac{n_i \cdot R \cdot T}{V}}\]

Per tant,

\[\displaystyle {P=\Sigma p_i= \frac{\Sigma n_i \cdot R \cdot T}{V}}\]

Exemple:

\[
\displaystyle
{
5 mols \, O_2, \, 3 mols \, H_2, \, 1 mol \, N_2
\\[0.5cm]
V= 10L, \, T=250K
\\
p_{ O_2 }= \frac { 5 \cdot 0.082 \cdot 250} { 10 }=\frac { 41 } { 4 }\, atm
\\
p_{ H_2 }= \frac { 3 \cdot 0.082 \cdot 250} { 10 }=\frac { 123 } { \, 20 }\, atm
\\
p_{ O_2 }= \frac { 5 \cdot 0.082 \cdot 250} { 10 }=\frac { 41 } { 4 }\, atm
\\
P=\frac { 41 } { 4 }+\frac { 123 } { \, 20 }+\frac { 41 } { 4 }=\mathbf {\frac { \,533} { 20 }\, atm}
}
\]

4.3.1.2 Llei de Boyle

A temperatura constant, el producte de la pressió d’un gas ideal pel volum és sempre constant: \[P \cdot V= constant\]

Exemple:

\[
\displaystyle
{
P_1=2 atm \enspace \, P_2=?
\\
V_1=5L \quad \quad V_2=3L
\\[0.5cm]
P_1 \cdot V_1=P_2 \cdot V_2 \rightarrow P_2=\frac{ P_1 \cdot V_1 } { \,\,V_2 }=\frac{ 2 \cdot 5 } { 3 }=\mathbf {\frac{10} {3} \, L}
}
\]

4.3.1.3 Llei de Gay-Lussac

La pressió que fa un gas ideal sobre les parets del recipient que el conté és proporcional a la temperatura del gas: \[\frac {P} {T}=constant \].

Exemple:

\[
\displaystyle{
P_1= ? \quad \quad \quad P_2=10 \, atm
\\
T_1=300K \quad T_2=450K
\\[0.5cm]
\frac {P_1} {T_1}=\frac{ P_2} { T_2} \rightarrow P_1=P_2 \cdot \frac { T_1 } { T_2 }=\frac{10 \cdot 300 } { 450 }=\mathbf {\frac{20} {3} \, atm}
}
\]

4.3.1.4 Llei de Charles (o dels volums)

A pressió constant, el volum és directament proporcional a la temperatura absoluta del gas:\[\frac{V}{T}=constant\]

Exemple:

\[
\displaystyle
{
T_1=225K \quad T_2=100K
\\
V_1=? \quad \quad \quad V_2=3L
\\[0.5cm]
\frac{V_1}{T_1}=\frac{V_2}{T_2} \rightarrow V_1=\frac{ V_2 \cdot T_1 }{ T_2 }=\frac{ 3 \cdot 225 }{ 100 }=\mathbf {\frac{27} {4} \,L}
}
\]

4.3.1.5 Lleis d’Avogadro (primera hipòtesi)

El volum ocupat per un gas ideal és proporcional al nombre de mols de gas:\[\frac{V}{n}=constant\]

Segons això, en condicions normals (0ºC, 1atm), el volum molar d’un gas és:

\[
\displaystyle{
\frac{ V } { n }=\frac{ R \cdot T } { ~P }=\frac{ 0.082 \cdot 273 } {1 }=22.386 \, L \cdot mol^{-1}
}
\]

4.3.1.6 Lleis dels gasos ideals o perfectes

De la combinació de les tres lleis anteriors es dedueix que la relació entre la pressió, el volum i la temperatura d’una massa de gas és:

\[
\displaystyle{
P \cdot V= k \cdot T \rightarrow \frac{ P \cdot V }{ T }=k \rightarrow \frac {P \cdot V }{ n \cdot T }=k
\\
{ P \cdot V }= n \cdot R \cdot T
}
\]

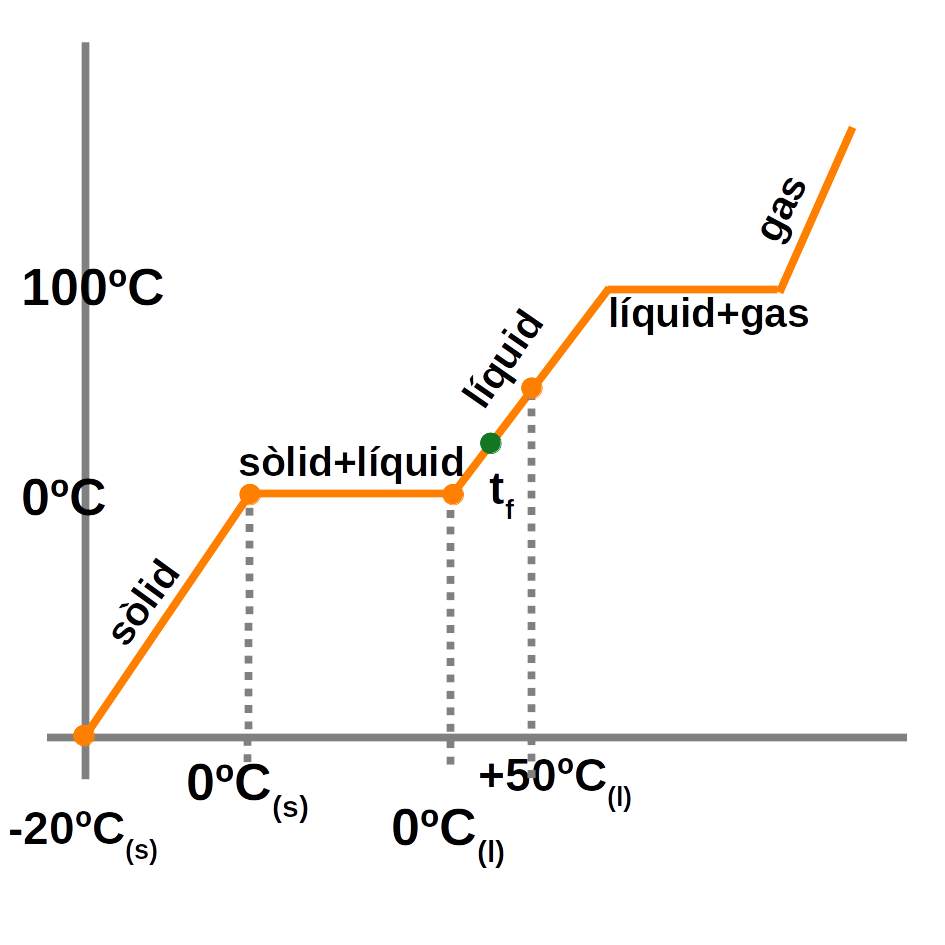
4.4 Canvis d’estat

Un canvi d’estat és una transformació física (no hi ha reacció química) en la qual una substància canvia l’estat d’agregació de les partícules mercès a l’absorció d’energia tèrmica.

Quan s’escalfa un sòlid (o un líquid), les partícules absorbeixen energia debilitant els enllaços i es forma l’estat líquid (o gasós). Si es refreda un líquid (o un gas), s’allibera energia i succeeix el procés invers.

Els canvis d’estat són:

• De sòlid a líquid: fusió
• De líquid a gas: evaporació
• De gas a líquid: condensació
• De líquid a sòlid: solidificació

Algunes substàncies passen de sòlid a gas sense passar per l’estat líquid. A aquest canvi d’estat se l’anomena sublimació directa. Al procés invers, se l’anomena sublimació inversa.

Mentre s’està produint un canvi d’estat, la temperatura no varia.

El bescanvi de calor entre estats es calcula fent:

\[Q=m \cdot c_e \cdot \Delta T\]

I en un canvi d’estat és:

\[Q=m \cdot \lambda\]

Exemple:

\[
\displaystyle{
\textbf{Calculeu la calor que cal per a escalfar un tros de gel de 500g de -20ºC a 50ºC.}
\\
C_e (gel) = \frac{0,5 cal} {\,g \cdot ºC}
\\
\lambda_f ( gel )=334 KJ/Kg
\\
C_e ( aigua )= \frac{ 1 cal } { g \cdot ºC }
\\[0.5cm]
Q_{total}=Q_{ (-20ºC a 0ºC) }+Q_{fusió}+Q_{( 0ºC a 50ºC )}
\\
a. \, Q_{ (-20ºC \,a \,0ºC) }=m_{gel} \cdot c_e( gel ) \cdot \Delta T=500g \cdot 0.5 \frac{ cal } { g \cdot ºC } \cdot ( 0-(-20) )=5 000 \,cal
\\[0.5cm]
b. \, Q_{fusió}=m ( gel ) \cdot \lambda_f( gel )=500 \,g \cdot 80.16 { cal } { \,g }=40 080 \,cal
\\
[\frac{334{ KJ }} { Kg } \cdot {\frac{1 000 J} {\, 1 KJ}} \cdot {\frac{0.24 \,cal } { \,1 J }} \cdot { \frac{\,1 Kg } { 1 000 g} }=80.16 \frac{ cal } { \,g }]
\\[0.5cm]
c. \,Q_{( 0ºC \,a \,50ºC )}=m_{aigua} \cdot c_e( aigua ) \cdot \Delta T=500g \cdot {1\frac{ \,cal } { g \cdot ºC }} \cdot ( 50-0 )=25 000 \,cal
\\[0.5cm]
Q_{total}=5 000+40 080+25 000=\mathbf{70 080 \,cal.}
}
\]

\[
\displaystyle{
\textbf{Calculeu la temperatura final quan un tros de ferro a 50ºC de 200g }
\\
\textbf{s’introdueix en 100ml d’aigua a 10ºC.}
\\
C_e(ferro)=450{\frac {\,\,J} {Kg \cdot K }}
\\
C_e( aigua )=4 180 {\frac {\,\,J} {Kg \cdot K }}
\\[0.5cm]
\textbf{El calor cedit pel ferro (-) és absorbit per l’aigua (+):}
\\
-Q_{ferro}=-m_{ferro} \cdot c_e( ferro ) \cdot \Delta T=-0.2 Kg \cdot 450{\frac {\,\,J} {Kg \cdot K }} \cdot ( t_f-323 )=29 070-90t_f
\\
+Q_{aigua}=+m_{aigua} \cdot c_e( aigua ) \cdot \Delta T
\\
0.1Kg \cdot 4180 { \frac{\,\,J } { Kg \cdot K} } \cdot ( t_f-283 )=418t_f-118294
\\
-Q_{ferro}=+Q_{aigua} \rightarrow 29070-90t_f=418t_f-118294
\\
t_f=\mathbf {290.1K\, (17.1ºC)}
}
\]

---